Método de Parametrización de la Frontera

El método de parametrización de la frontera es una estrategia empleada para determinar los valores máximo y mínimo absolutos de una función de dos variables en una región cerrada y acotada.

Cuando los puntos críticos interiores no existen o no bastan para caracterizar los extremos, resulta necesario estudiar la función a lo largo de la frontera del dominio.

No obstante, en la frontera no puede aplicarse el método estándar de puntos críticos (basado en derivadas parciales), ya que dichos puntos quedan fuera del interior del dominio.

Es en este contexto donde la parametrización resulta esencial.

¿Cuál es la idea?

Supongamos que trabajamos con una función $f(x, y)$ definida en un dominio $A$ cuya frontera es curva o bien poligonal. Para analizar $f$ en esa frontera seguimos los pasos siguientes:

1. Dividir la frontera en segmentos más sencillos.
2. Expresar cada segmento de forma paramétrica como una curva o recta: $ (x(t), y(t)) $ con $ t \in [a, b] $. Así el problema se reduce a una función de una sola variable en términos de $t$.
3. Determinar los extremos locales de $f$ en cada segmento analizando la función resultante en una variable.
4. Evaluar $f$ en todos los puntos críticos obtenidos y decidir cuáles corresponden al máximo y al mínimo global.

Por ejemplo, para estudiar la función $f(x, y) = x^2 + y^2$ sobre la frontera de la circunferencia $x^2 + y^2 = 1$, podemos parametrizarla como: $$ x(t) = \cos t,\quad t \in [0, 2\pi] $$ $$ y(t) = \sin t,\quad t \in [0, 2\pi] $$ Al componer $f$ con la parametrización se obtiene: $$ g(t) = f(\cos t, \sin t) = \cos^2 t + \sin^2 t = 1 $$

Un ejemplo concreto

Consideremos la función

$$ f(x,y) = x^2 + 2y $$

en la región cerrada y acotada

$$ A = \{(x,y) \in \mathbb{R}^2 \mid x^2 - 1 \le y \le 3 \} $$

Queremos determinar sus valores máximo y mínimo absolutos.

Dado que $A$ es cerrada y acotada, el teorema de Weierstrass garantiza la existencia de extremos absolutos.

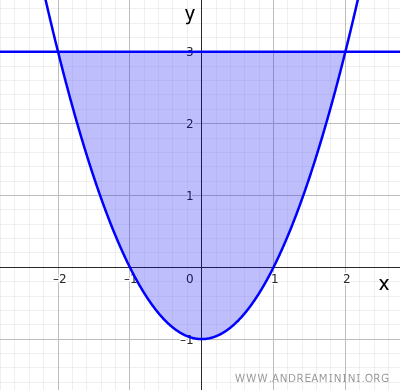
Analizaremos la función tanto en el interior del dominio como en su frontera.

1] Puntos críticos interiores

Los puntos críticos interiores incluyen los estacionarios -donde el gradiente se anula- y los singulares -donde el gradiente no existe-.

Calculemos las derivadas parciales:

$$ f_x = 2x $$

$$ f_y = 2 $$

El sistema que resuelve los puntos estacionarios es:

$$
\begin{cases}
f_x = 0 \Rightarrow x = 0 \\
f_y = 0 \Rightarrow 2 = 0
\end{cases}
$$

Este sistema carece de solución, de modo que no existen puntos estacionarios en el interior.

Además, la función es diferenciable en todo $\mathbb{R}^2$, por lo que tampoco hay puntos singulares.

2] Estudio de la frontera

La frontera está formada por dos partes: un segmento recto y una parábola.

• Segmento 1: La parte superior corresponde a la recta $y = 3$ con $x \in [-2, 2]$. Una parametrización adecuada es $(t, 3)$ con $t \in [-2, 2]$. Sustituyendo en $f$ se obtiene: $$ g(t) = f(t, 3) = t^2 + 6 $$ El mínimo se alcanza en $$t = 0 \Rightarrow f(0, 3) = 6$$ y el máximo en $$t = \pm 2 \Rightarrow f(\pm 2, 3) = 10$$ Este tramo proporciona tres puntos candidatos: $(0, 3)$, $(-2, 3)$ y $(2, 3)$.
  
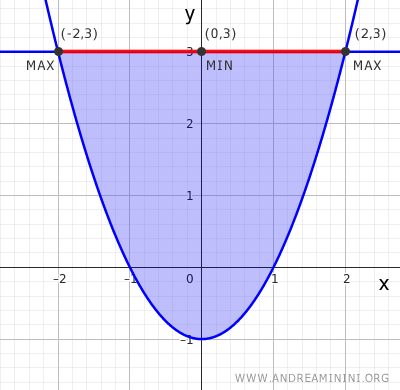
• Segmento 2: El otro componente de la frontera es la parábola $y = x^2 - 1$ con $x \in [-2, 2]$. Puede parametrizarse como $(t, t^2 - 1)$ con $t \in [-2, 2]$. Sustituyendo obtenemos: $$ g(t) = f(t, t^2 - 1) = t^2 + 2(t^2 - 1) = 3t^2 - 2 $$ El mínimo aparece en $$t = 0 \Rightarrow f(0, -1) = -2$$ y el máximo en $$t = \pm 2 \Rightarrow f(\pm 2, 3) = 10$$ Este tramo aporta otros tres puntos candidatos: $(0, -1)$, $(-2, 3)$ y $(2, 3)$.

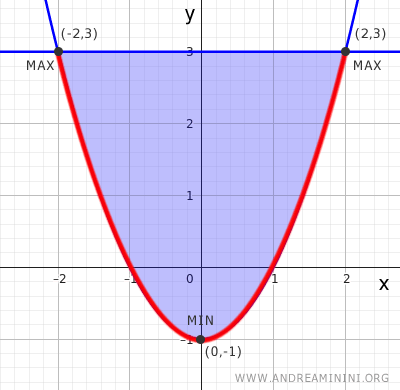
Evaluamos ahora la función en todos los candidatos:

$$
\begin{align*}
f(-2, 3) &= 4 + 6 = 10 \\
f(2, 3) &= 4 + 6 = 10 \\
f(0, 3) &= 0 + 6 = 6 \\
f(0, -1) &= 0 - 2 = -2
\end{align*}
$$

En consecuencia, el máximo absoluto de $f$ es 10, alcanzado en $(-2, 3)$ y $(2, 3)$.

El mínimo absoluto es $-2$, alcanzado en $(0, -1)$.

Cómo parametrizar tramos de frontera

La elección de la parametrización adecuada depende de la geometría del tramo considerado.

• Circunferencia
  Para parametrizar una circunferencia de radio $r$ centrada en el origen: $$ x(t) = r \cos t,\quad y(t) = r \sin t,\quad t \in [0, 2\pi] $$ Si está centrada en $(a, b)$: $$ x(t) = a + r \cos t,\quad y(t) = b + r \sin t $$
• Elipse
  Para una elipse centrada en el origen: $$ x(t) = a \cos t,\quad y(t) = b \sin t,\quad t \in [0, 2\pi] $$ Si se traslada a $(x_0, y_0)$: $$ x(t) = x_0 + a \cos t,\quad y(t) = y_0 + b \sin t $$
• Segmentos de recta
  Para parametrizar el segmento entre $P = (x_1, y_1)$ y $Q = (x_2, y_2)$: $$ x(t) = (1 - t)x_1 + t x_2,\quad y(t) = (1 - t)y_1 + t y_2,\quad t \in [0, 1] $$
• Hipérbola
  Para una hipérbola como $\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$: $$ x(t) = a \cosh t,\quad y(t) = b \sinh t,\quad t \in \mathbb{R} $$
• Espirales
  En la espiral de Arquímedes: $$ x(t) = a t \cos t,\quad y(t) = a t \sin t,\quad t \in [0, 2\pi] \text{ o más allá} $$
• Curvas especiales
  Para arcos de curvas como $y = \sqrt{x}$, basta con elegir $t$ en el intervalo apropiado y sustituir: $x = t$, $y = \sqrt{t}$.

La idea general es siempre la misma: describir el recorrido como $x(t), y(t)$ dejando que $t$ recorra el intervalo adecuado.

Y así sucesivamente.