Puntos aislados de un conjunto
Sea \( x_0 \) un número real que pertenece a un subconjunto \( A \subset \mathbb{R} \). Se dice que el punto \( x_0 \) es un punto aislado del conjunto \( A \) si existe al menos un entorno de \( x_0 \) que no contiene elementos de \( A \) distintos del propio \( x_0 \).
Desde una perspectiva intuitiva, esto significa que alrededor de \( x_0 \) puede elegirse un intervalo lo suficientemente pequeño como para que su intersección con el conjunto \( A \) se reduzca únicamente al punto \( x_0 \).
Un entorno de \( x_0 \) es un intervalo abierto de la forma
\[ I = (x_0 - r,\; x_0 + r) \]
donde \( r > 0 \) es un número real positivo.
El punto \( x_0 \) es aislado si existe al menos un valor de \( r \) tal que
\[ I \cap A = \{x_0\} \]
No es necesario que esta condición se verifique para todos los entornos de \( x_0 \). Basta la existencia de un solo entorno que cumpla dicha propiedad.
Cómo determinar si un punto es aislado
Para establecer si un punto \( x_0 \) es aislado:
- se parte de un punto que pertenezca al conjunto \( A \);
- se identifica al menos un entorno de \( x_0 \) que no contenga otros puntos de \( A \);
- si dicho entorno existe, el punto es aislado. En cambio, si todo entorno contiene otros puntos del conjunto, el punto no es aislado.
Un ejemplo concreto
Consideremos el conjunto \( A \), definido como una sucesión de números racionales
\[ A = \left\{ 0, \frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \dots , \frac{n}{n+1} \right\} \]
donde \( n \) es un número natural arbitrario.
Representamos este conjunto en la recta real y fijamos la atención en el punto \( 0 \).
Se puede encontrar un entorno de \( 0 \) que no contenga otros elementos de \( A \), por ejemplo \( \left(-\frac{1}{3}, \frac{1}{3}\right) \).
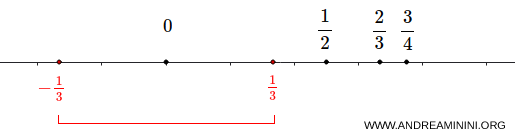
Por lo tanto, \( 0 \) es un punto aislado del conjunto \( A \).
Mediante el mismo razonamiento, y escogiendo entornos suficientemente pequeños, se puede demostrar que todos los elementos del conjunto \( A \) son puntos aislados.
Notas
Algunas observaciones y precisiones adicionales sobre los puntos aislados
- Conjuntos finitos
Si un conjunto contiene un número finito de puntos, entonces todos ellos son puntos aislados. Por ejemplo \[ B = \{-1,\; 0,\; \tfrac{3}{5},\; 6\} \] Este conjunto consta de cuatro puntos distintos. Para cada uno de ellos puede construirse un entorno lo suficientemente pequeño como para excluir a todos los demás. - Conjuntos infinitos formados exclusivamente por puntos aislados
Un conjunto puede ser infinito y, sin embargo, estar compuesto únicamente por puntos aislados. Por ejemplo, el conjunto de los números naturales es infinito y cada número natural es un punto aislado \[ \mathbb{N} = \{0,1,2,3,\dots\} \] Para cada número natural \( n \) basta considerar un entorno de radio \( \tfrac{1}{2} \), que no contiene ningún otro número natural. \[ (n-\tfrac{1}{2},\; n+\tfrac{1}{2}) \] En consecuencia, todos los números naturales son puntos aislados. - Un punto aislado nunca es un punto de acumulación
Por definición, siempre existe una región alrededor de un punto aislado en la que el conjunto no contiene otros elementos. Esta distinción es fundamental en el estudio de los límites de funciones y en el análisis de la estructura local de los subconjuntos de la recta real.
Y así sucesivamente.