Funciones monótonas
¿Qué es una función monótona?
- En matemáticas, una función $f(x)$ se denomina monótona en un intervalo $[a, b]$ cuando, para cualesquiera dos valores $x_1$ y $x_2$ de dicho intervalo, con $x_2 > x_1$, se cumple una de las siguientes condiciones:
- Creciente: $$ f(x_1) \le f(x_2) $$
- Estrictamente creciente: $$ f(x_1) < f(x_2) $$
- Decreciente: $$ f(x_1) \ge f(x_2) $$
- Estrictamente decreciente: $$ f(x_1) > f(x_2) $$
Ejemplos
Ejemplo 1
La siguiente función es monótonamente creciente.
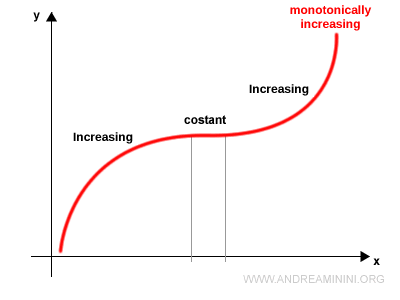
No obstante, no es estrictamente creciente, ya que en algunos tramos permanece constante.
En lenguaje técnico, se clasifica como una función no decreciente.
Ejemplo 2
Esta función es estrictamente creciente, pues aumenta de manera continua y nunca se mantiene constante.
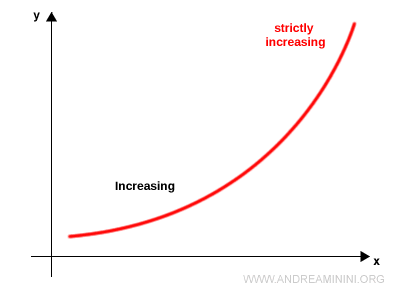
Ejemplo 3
La siguiente función es monótonamente decreciente.
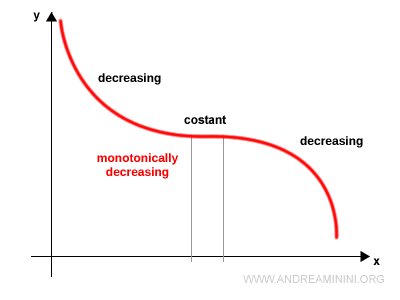
Tampoco es estrictamente decreciente, porque en ciertos intervalos su valor se mantiene constante.
Por ello se la considera una función no creciente.
Ejemplo 4
En este caso, la función es estrictamente decreciente, ya que desciende de forma continua sin presentar tramos planos.
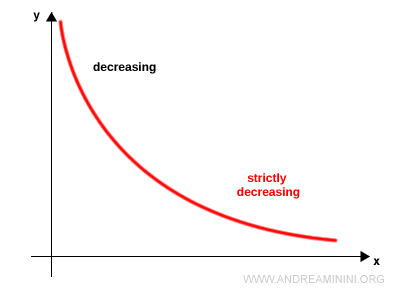
Funciones estrictamente monótonas
Una función es estrictamente monótona cuando resulta estrictamente creciente o estrictamente decreciente en todo su dominio.
Dicho de otro modo, una función estrictamente monótona nunca presenta intervalos constantes: siempre crece o siempre decrece.
Propiedades fundamentales de las funciones estrictamente monótonas
La estricta monotonía ocupa un lugar esencial en el análisis matemático, ya que garantiza la invertibilidad de la función.
Toda función estrictamente monótona es invertible, es decir, admite siempre una función inversa.
Ejemplo
La función $f(x) = x + 1$ es estrictamente creciente:
$$ f(x) = x+1 $$
Por lo tanto, también es invertible, y su inversa está dada por:
$$ f^{-1}(y) = y - 1 $$
Este principio se cumple de manera general para todas las funciones estrictamente monótonas.