Funciones decrecientes

Se dice que una función $y = f(x)$ es decreciente en un intervalo $I = (a, b)$ cuando, para cualesquiera dos puntos $x_1$ y $x_2$ de dicho intervalo, con $x_1 < x_2$, se cumple: $$ f(x_1) \ge f(x_2) $$. Se llama estrictamente decreciente cuando: $$ f(x_1) > f(x_2) $$

Una función estrictamente decreciente también suele describirse como decreciente en sentido estricto.

Tanto las funciones decrecientes como las estrictamente decrecientes forman parte de la familia más amplia de las funciones monótonas.

Nota: Una función es monótona en un intervalo de su dominio cuando mantiene un comportamiento uniforme, ya sea creciente o decreciente, en todo el intervalo.

Ejemplo

Consideremos la función:

$$ y = x^2 $$

Esta función es estrictamente decreciente en el intervalo $(-4, 0)$, pues para cualesquiera dos puntos $x_1$ y $x_2$ en ese intervalo, con $x_1 < x_2$, se cumple que $f(x_1) > f(x_2)$.

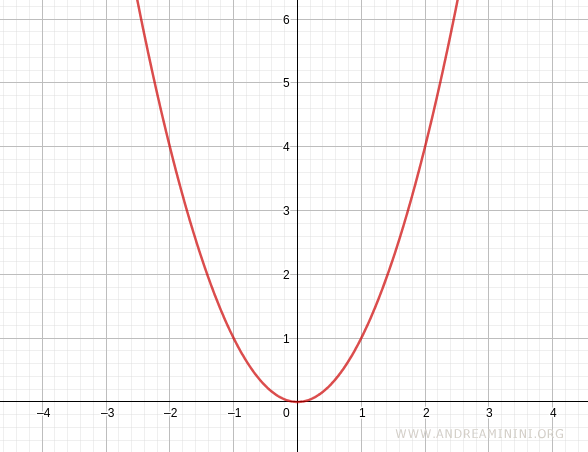
En cambio, la misma función no es decreciente en el intervalo $(0, 4)$.

Nota: En el caso de funciones continuas y derivables, el carácter decreciente puede determinarse analizando el signo de la primera derivada, $f'(x)$.

Y así sucesivamente.