Funciones Polinómicas

¿Qué es una función polinómica?

Se denomina función polinómica a toda función cuya expresión está definida por un polinomio: $$ y = P(x) $$

Un ejemplo de función polinómica es:

$$ f(x) = x^3 - x^2 - 2x + 2 $$

En este caso, la función está determinada por el polinomio P(x) = x³ - x² - 2x + 2, un polinomio de tercer grado en una sola variable.

Al sustituir distintos valores de la variable independiente $ x $ - cuyo dominio es el conjunto de los números reales - podemos calcular los valores correspondientes de la función $ y = f(x) $.

Veamos la evaluación de la función alrededor del punto $ x = 0 $:

$$ \begin{array}{c|lcr} x & \text{y} \\ \hline -3 & -28 \\ -2 & -6 \\ -1 & 2 \\ 0 & 2 \\ 1 & 0 \\ 2 & 2 \\ 3 & 14 \end{array} $$

Cada fila de la tabla representa un par de coordenadas $(x, y)$, es decir, un punto en el plano cartesiano.

Con esta información es posible esbozar una gráfica aproximada de la función en torno al intervalo considerado.

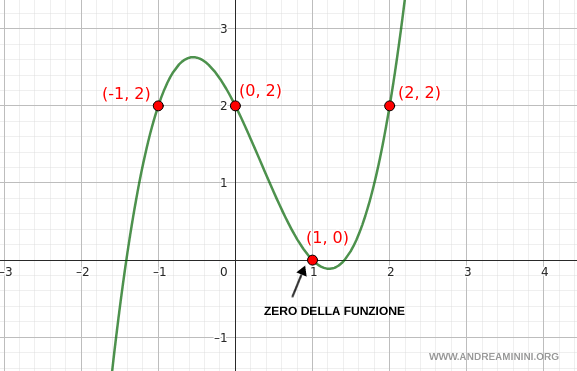
gráfica de una función polinómica cerca de x igual a cero

Los valores de $ x $ que anulan la función - es decir, aquellos para los que $ y(x) = 0 $ - se llaman raíces o ceros del polinomio.

En estos puntos, la gráfica de la función corta el eje x, pues el valor de salida es $ y = 0 $.

En el ejemplo mostrado, la función tiene una única raíz real en el punto $(1, 0)$, correspondiente al valor $ x = 1 $.

Nota: Una función polinómica puede tener una, varias o ninguna raíz real. En cambio, los valores de $ x $ para los que la función crece sin límite - ya sea hacia $ +\infty $ o hacia $ -\infty $ - reciben el nombre de polos.

Y así sucesivamente.