Análisis del signo de una función

En un intervalo dado, una función se considera positiva si f(x) > 0, negativa si f(x) < 0, y nula si f(x) = 0.

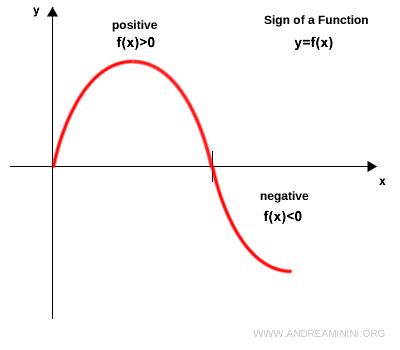
Para determinar dónde una función es positiva o negativa, basta localizar los puntos en los que su gráfica corta el eje x: son los llamados ceros de la función.

Nota. El análisis del signo forma parte del estudio de funciones, que abarca aspectos fundamentales como el dominio, los intervalos de crecimiento y decrecimiento, la concavidad y convexidad, los extremos locales, los puntos de inflexión y otras propiedades relevantes.

Un ejemplo concreto

Consideremos la función definida en el conjunto de los números reales:

$$ y = x^3 - 2x^2 - 3x $$

Su dominio es toda la recta real: (-∞, +∞).

Para hallar sus intersecciones con el eje x (es decir, sus ceros), resolvemos la ecuación y = 0:

$$ x^3 - 2x^2 - 3x = 0 $$

Extrayendo el factor común x, obtenemos:

$$ x(x^2 - 2x - 3) = 0 $$

Analizamos ahora el signo de cada factor: x y el trinomio cuadrático x² - 2x - 3.

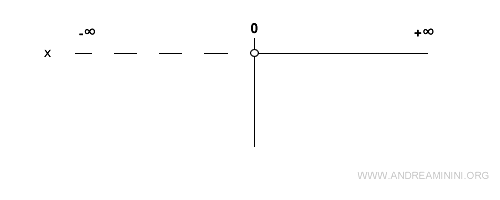
El signo del primer factor (x) es inmediato: resulta positivo para x > 0.

En el esquema, esto se representa con una línea continua en la región positiva y un círculo abierto en el cero x = 0.

El segundo factor es una expresión cuadrática. Aplicamos la fórmula general:

$$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$ $$ x = \frac{-(-2) \pm \sqrt{(-2)^2 - 4(1 \cdot -3)}}{2(1)} $$ $$ x = \frac{2 \pm \sqrt{16}}{2} $$ $$ x = \frac{2 \pm 4}{2} $$

De aquí se obtienen las raíces:

$$ x_1 = \frac{2 + 4}{2} = 3 \quad \text{y} \quad x_2 = \frac{2 - 4}{2} = -1 $$

Estudiamos ahora el signo del trinomio entre y fuera de estas raíces:

• En el intervalo (-1, 3), la cuadrática es negativa. Por ejemplo, en x = 0 se cumple f(x) < 0.
• En el intervalo (-∞, -1), resulta positiva. Por ejemplo, para x = -2 se obtiene f(x) = 5.
• En el intervalo (3, +∞), también es positiva. Por ejemplo, con x = 4 se cumple f(x) = 5.

Estos intervalos de signo y sus raíces se ilustran en el siguiente esquema:

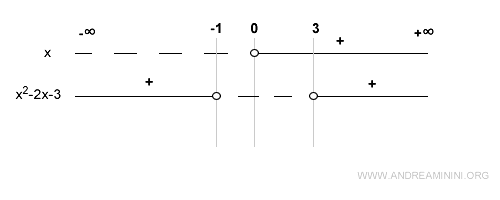
Como la función original es el producto de x y (x² - 2x - 3), el signo de f(x) se determina combinando los signos de ambos factores.

Por ejemplo, en el intervalo (-∞, -1), x es negativo y la cuadrática positiva.

En consecuencia, el producto es negativo:

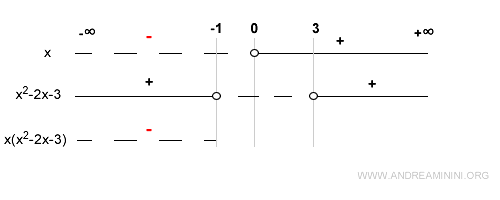
En x = -1, la cuadrática se anula y el producto también es cero:

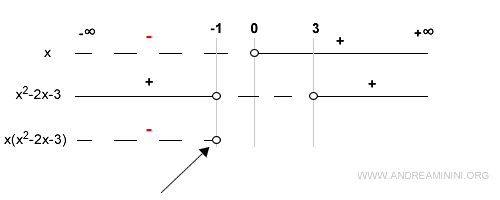
En el intervalo (-1, 0), ambos factores son negativos, por lo que su producto es positivo:

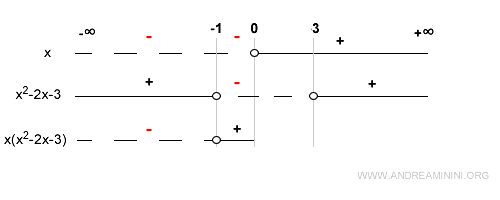
En x = 0, el primer factor se anula y la función vale cero: otro cero de f.

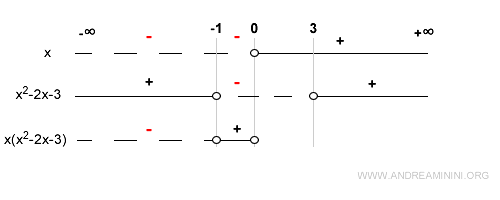
En el intervalo (0, 3), x es positivo y la cuadrática negativa, de modo que el producto resulta negativo: aquí f(x) < 0.

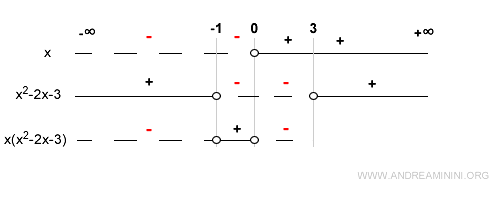
En x = 3, la cuadrática vuelve a anularse, por lo que f también es cero: tercer cero de la función.

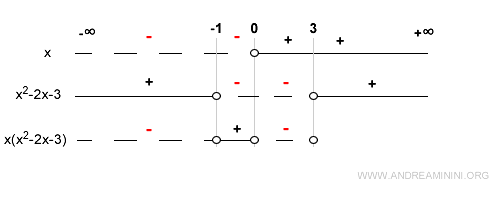
Finalmente, en el intervalo (3, +∞), ambos factores son positivos y su producto también: f(x) > 0.

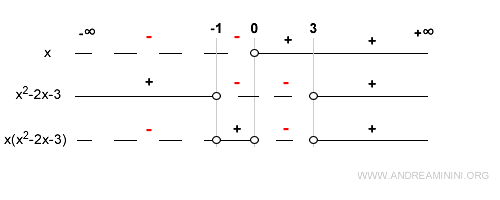
Este esquema final resume los intervalos en los que la función f(x) = x(x² - 2x - 3) es positiva o negativa e indica sus ceros.

En síntesis: la función es negativa en (-∞, -1), positiva en (-1, 0), negativa en (0, 3) y positiva en (3, +∞).

A continuación se muestra la gráfica de la función para verificar visualmente el análisis:

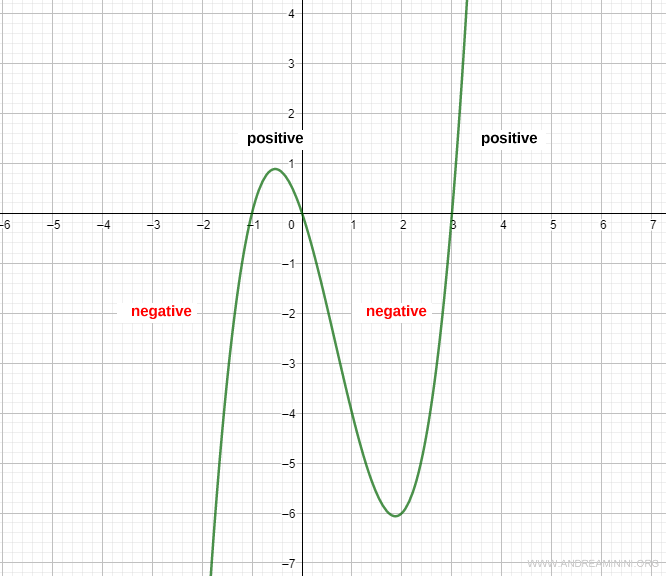
Y así sucesivamente.