Funciones inyectivas
¿Qué es una función inyectiva?
Una función matemática $f(x)$ se denomina inyectiva cuando a elementos distintos del dominio les corresponden imágenes distintas en el codominio: $$ \text{si } x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) $$ De forma equivalente, si dos entradas son iguales, sus imágenes también coinciden: $$ \text{si } x_1 = x_2 \Rightarrow f(x_1) = f(x_2) $$
Los diagramas de Venn permiten visualizar este concepto de manera sencilla e intuitiva.
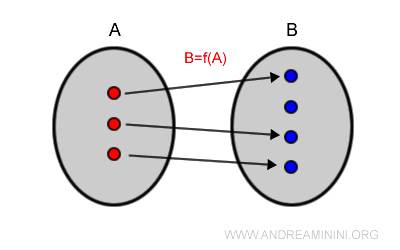
En otras palabras, una función de A en B es inyectiva cuando cada elemento de A se asocia con un único elemento distinto de B.
Aquí, el conjunto A representa el dominio de la función $f(x)$ y el conjunto B el codominio.
Nota. La definición formal de inyectividad se expresa así: $$ \forall x_1, x_2 \in D_f \mid x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) $$ Es decir, para cualquier par de valores distintos $x_1$ y $x_2$ en el dominio $D_f$, las imágenes también deben ser distintas: $f(x_1) \ne f(x_2)$.
Conviene destacar que el conjunto B no siempre coincide con el verdadero codominio. Es posible que algunos elementos de B no sean imagen de ningún elemento de A.
En esos casos, el codominio efectivo (C) de la función resulta ser un subconjunto propio de B.
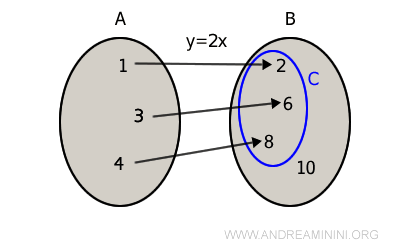
Un ejemplo práctico
Ejemplo 1
La siguiente función, definida sobre el conjunto de los números reales ℝ, es inyectiva:
$$ f(x) = x + 1 $$
En efecto, para cada $x \in \mathbb{R}$, la salida $f(x)$ es única y distinta de la correspondiente a cualquier otra entrada.
| x | y = f(x) |
|---|---|
| -3 | -2 |
| -2 | -1 |
| -1 | 0 |
| 0 | 1 |
| 1 | 2 |
| 2 | 3 |
| 3 | 4 |
Cada valor de entrada $x$ en el dominio genera una salida diferente $y = f(x)$.
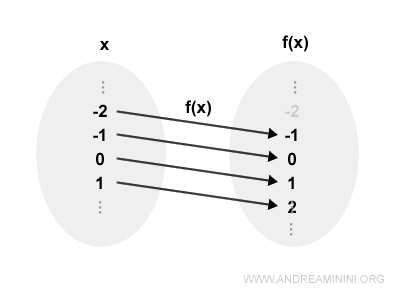
Nota. Desde el punto de vista gráfico, una función es inyectiva si cualquier recta horizontal corta a su gráfica como máximo en un punto. Dicho de otro modo: o la toca una sola vez, o no la corta en absoluto.
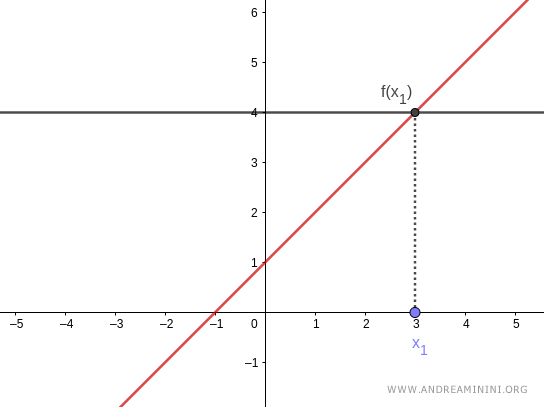
Esto refleja la idea de que cada $x$ del dominio se corresponde con un único valor $y$ en el codominio.
Ejemplo 2
La siguiente función no es inyectiva:
$$ f(x) = x^2 $$
Aquí, entradas distintas pueden dar lugar a la misma salida.
| x | y = f(x) |
|---|---|
| -3 | 9 |
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
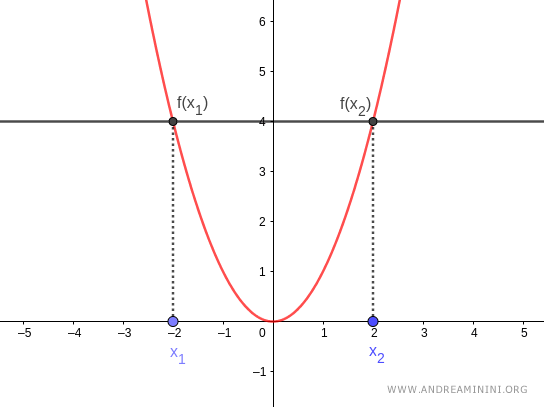
Por ejemplo, $f(-2) = f(2) = 4$, lo cual muestra que la función no cumple la condición de inyectividad.
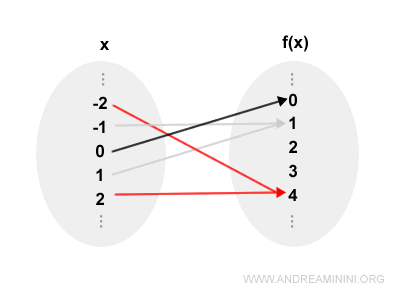
Nota. Gráficamente, una función no es inyectiva si existe al menos una recta horizontal que corta a su gráfica en más de un punto. En tal caso, hay dos o más valores distintos de entrada que comparten la misma salida.
Y así sucesivamente.