Función discontinua
Se dice que una función $f(x)$ es discontinua en un punto $x_0$ cuando el límite de $f(x)$ al aproximarse $x$ a $x_0$ no coincide con el valor que la función toma en ese punto: $$ \lim_{x \rightarrow x_0} f(x) \ne f(x_0) $$ Ese punto $x_0$ recibe el nombre de punto de discontinuidad.
Ejemplo de función discontinua
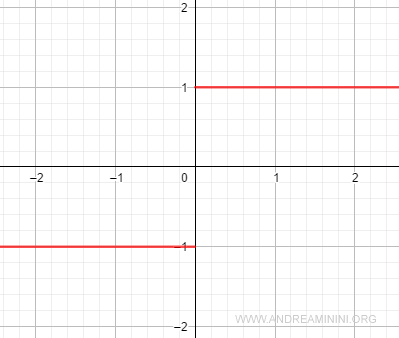
Discontinuidades eliminables y no eliminables
- Una discontinuidad es eliminable si puede corregirse redefiniendo convenientemente la función para que resulte continua.
- Se denomina no eliminable cuando no existe forma de suprimirla mediante una redefinición local.
¿Por qué aparecen las discontinuidades?
Las discontinuidades pueden producirse por diversas razones, según el comportamiento de la función en torno al punto en cuestión:
Discontinuidad de salto (primera especie)
En $x_0$, el límite lateral derecho y el límite lateral izquierdo de la función no coinciden. A este caso se le llama discontinuidad de salto o discontinuidad de primera especie: $$ \lim_{x \rightarrow x_0^+} f(x) \ne \lim_{x \rightarrow x_0^-} f(x) $$
La función puede estar definida o no en $x_0$.
Ejemplo
La función signo presenta una discontinuidad en $x_0 = 0$:
$$ \frac{|x|}{x} $$
ya que los límites laterales son diferentes:
$$ \lim_{x \rightarrow 0^+} \frac{|x|}{x} = 1 $$
$$ \lim_{x \rightarrow 0^-} \frac{|x|}{x} = -1 $$
Gráficamente se observa:
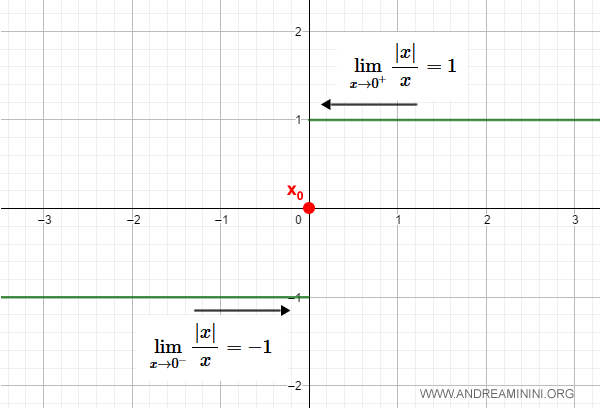
En $x_0$ la función pasa bruscamente de $-1$ a $+1$.
Discontinuidad esencial (segunda especie)
En $x_0$, al menos uno de los límites laterales es infinito o no existe. A esta situación se la denomina discontinuidad esencial o discontinuidad de segunda especie: $$ \lim_{x \rightarrow x_0^±} f(x) \ne f(x_0) = \{ ±\infty , \text{no existe} \} $$
Ejemplo
La función $$ \frac{1}{x} $$ es discontinua en $x_0 = 0$,
porque el límite lateral derecho tiende a infinito:
$$ \lim_{x \rightarrow 0^+} = +\infty $$
Nota. En este caso, el límite lateral izquierdo tiende a menos infinito: $$ \lim_{x \rightarrow 0^-} = -\infty $$ En general, se habla de discontinuidad de segunda especie cuando al menos uno de los límites laterales diverge ($±\infty$) o no está definido.
La gráfica es la siguiente:
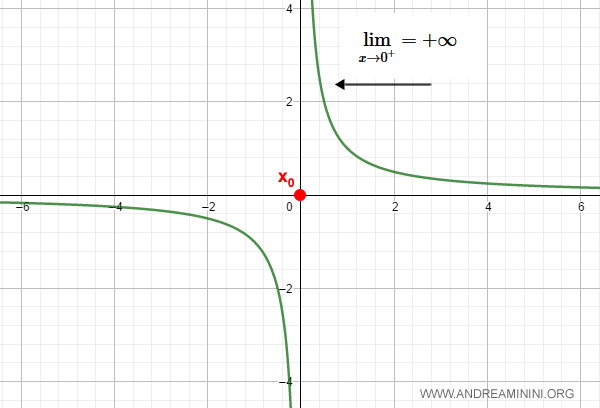
Discontinuidad evitable (tercera especie)
En $x_0$, el límite de la función existe pero no coincide con el valor que la función adopta en ese punto: $$ \lim_{x \rightarrow x_0} f(x) \ne f(x_0) $$
Se denomina discontinuidad evitable, ya que puede resolverse redefiniendo el valor de la función en $x_0$ para que coincida con el límite.
Este tipo de discontinuidad aparece con frecuencia en funciones definidas por tramos.
Ejemplo
Consideremos la función:
$$ f(x) = \frac{\sin x}{x} $$
En $x_0 = 0$ la función no está definida, pero el límite sí existe:
$$ \lim_{x \rightarrow 0} \frac{\sin x}{x} = 1 $$
Este es un límite muy conocido.
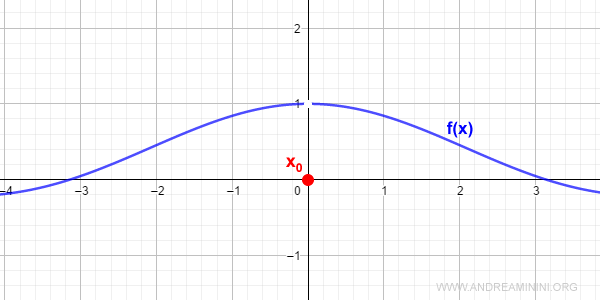
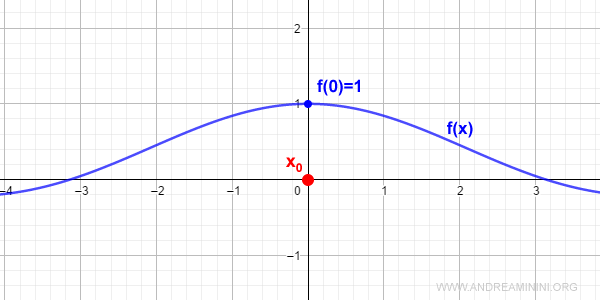
La discontinuidad puede eliminarse definiendo $f(0) = 1$:
$$ f(x) = \begin{cases} \frac{\sin x}{x} \: \text{si} \: x \ne 0 \\ 1 \: \text{si} \: x = 0 \end{cases} $$
Con esta redefinición la función se hace continua:
Ejemplo 2
Veamos ahora esta función definida por tramos:
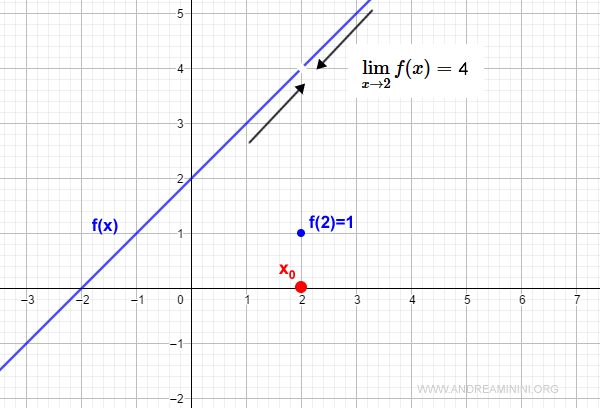
$$ f(x) = \begin{cases} x+2 \: \text{si} \: x \ne 2 \\ 1 \: \text{si} \: x = 2 \end{cases} $$
Esta función presenta una discontinuidad en $x_0 = 2$.
El límite cuando $x$ tiende a 2 existe:
$$ \lim_{x \rightarrow 2} f(x) = 4 $$
Es decir, los límites laterales son iguales.
Sin embargo, el valor de la función en $x=2$ es:
$$ f(2) = 1 $$
Por lo tanto, aunque el límite en $x_0$ existe, la función adopta un valor distinto.
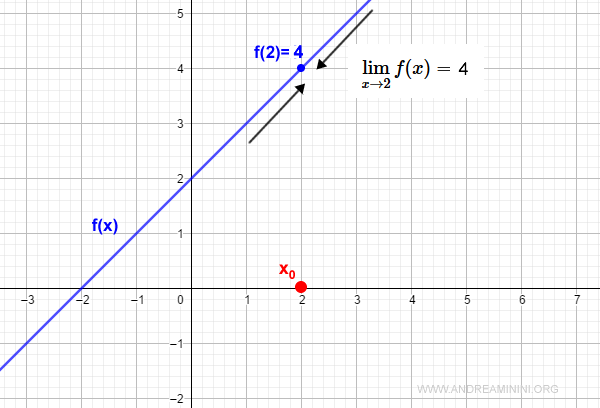
Para eliminar esta discontinuidad basta redefinir la función así:
$$ f(x) = \begin{cases} x+2 \: \text{si} \: x \ne 2 \\ 4 \: \text{si} \: x = 2 \end{cases} $$
De esta manera la función se vuelve continua:
Y así sucesivamente.