Asíntotas

Definición de asíntota

En matemáticas, una asíntota es una recta o una curva hacia la que la gráfica de una función se aproxima cada vez más. Esta aproximación puede ocurrir cuando la variable independiente x tiende a ±infinito o cuando se acerca a un valor finito concreto.

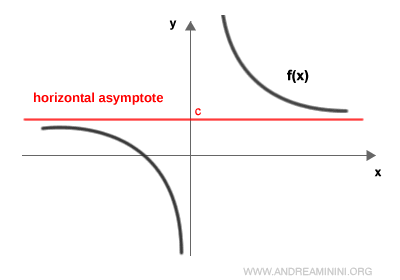
Desde un punto de vista más formal, una recta es una asíntota si la distancia entre la gráfica de la función y dicha recta tiende a 0 cuando x tiende a infinito o a un límite finito.

En otras palabras, la gráfica se va acercando progresivamente a la recta, hasta quedar tan próxima como se desee.

• Si la asíntota es una recta, se denomina asíntota lineal.
• Si la asíntota es una curva, se denomina asíntota curvilínea.

En análisis matemático, al estudiar una función f(x), se distinguen tres tipos principales de asíntotas: horizontales, verticales y oblicuas.

Asíntotas horizontales

Una asíntota horizontal se determina evaluando el límite de la función cuando x tiende a más o menos infinito:

$$ \lim_{x \rightarrow ±∞ } f(x) = c $$

La asíntota horizontal existe si este límite es un número real finito.

Veamos un ejemplo sencillo de asíntota horizontal:

En la práctica, una asíntota horizontal es una recta paralela al eje x o coincidente con él.

Conviene destacar que las asíntotas horizontales para x → +∞ y para x → -∞ no tienen por qué coincidir.

Ejemplo

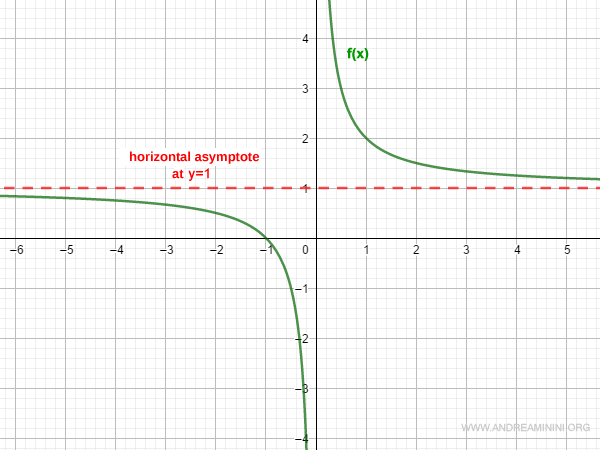
Busquemos las asíntotas horizontales de la función:

$$ f(x) = \frac{x+1}{x} $$

Calculamos primero el límite cuando x → +∞:

$$ \lim_{x \rightarrow +∞ }\frac{x+1}{x} = 1 $$

La función, por tanto, tiene una asíntota horizontal en y = 1 para x → +∞.

Nota. Este caso corresponde a una indeterminación del tipo ∞/∞, que puede resolverse aplicando la Regla de L'Hôpital.

Ahora evaluamos el límite cuando x → -∞:

$$ \lim_{x \rightarrow -∞ }\frac{x+1}{x} = 1 $$

Por consiguiente, la función también presenta una asíntota horizontal en y = 1 para x → -∞.

 

Asíntotas verticales

Una asíntota vertical aparece en los puntos donde la función no está definida. Se identifica evaluando el límite de f(x) cuando x se aproxima a x₀ por la derecha y por la izquierda: $$ \lim_{x \rightarrow x_0^+ } f(x) = ±∞ $$ $$ \lim_{x \rightarrow x_0^- } f(x) = ±∞ $$ donde x₀ es un punto de discontinuidad.

Existe una asíntota vertical en x₀ si dichos límites tienden a más o menos infinito.

He aquí un ejemplo práctico de asíntota vertical:

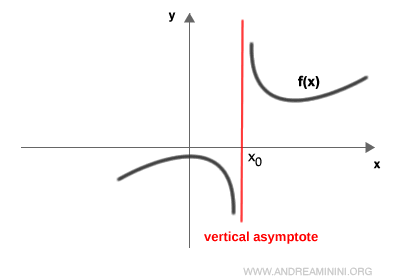
En la práctica, una asíntota vertical es una recta paralela al eje y o coincidente con él.

Ejemplo

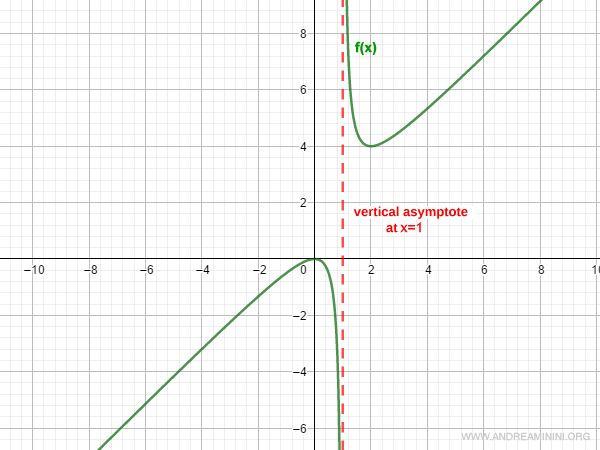
Analicemos si la siguiente función presenta alguna asíntota vertical:

$$ f(x) = \frac{x^2}{x-1} $$

La función no está definida en x = 1.

Estudiamos el límite cuando x tiende a 1 por ambos lados:

$$ \lim_{x \rightarrow 1^+ } \frac{x^2}{x-1} = +∞ $$

$$ \lim_{x \rightarrow 1^- } \frac{x^2}{x-1} = -∞ $$

De este modo, la función posee una asíntota vertical en x = 1.

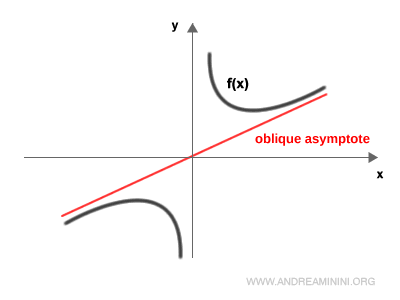
Asíntotas oblicuas

Una función presenta una asíntota oblicua cuando, al crecer x sin límite hacia +∞ o hacia -∞, la diferencia entre la función $ f(x) $ y la recta $ y = mx + q $ tiende a cero: $$ \lim_{x \rightarrow \pm \infty} \left[ f(x) - (mx + q) \right] = 0 $$ En términos geométricos, esto significa que la gráfica de la función se aproxima cada vez más a la recta $ y = mx + q $ a medida que nos alejamos hacia los extremos del eje x. Si la función admite una asíntota oblicua de ecuación $ y = mx + q $, la pendiente $ m \ne 0 $ y la ordenada en el origen $ q $ son valores finitos que pueden calcularse de la siguiente manera: $$ m = \lim_{x \to \infty} \frac{f(x)}{x} $$ $$ q = \lim_{x \to \infty} \left[ f(x) - mx \right] $$

Estos límites permiten determinar de forma precisa la recta a la que la función se aproxima en el infinito.

Veamos un ejemplo ilustrativo de asíntota oblicua:

Para comprobar si existe una asíntota oblicua cuando x → +∞, calculamos primero la pendiente m:

$$ m = \lim_{x \rightarrow +∞ } \frac{f(x)}{x} \ne 0 $$

Demostración. Si $$ \lim_{x \rightarrow +∞ } f(x) - (mx+q) = 0 $$ podemos fijar inicialmente q = 0 y calcular: $$ \lim_{x \rightarrow +∞ } f(x) - mx = 0 $$ Como el límite tiende a cero para x → ∞, es válido dividir entre x: $$ \lim_{x \rightarrow +∞ } \frac{f(x) - mx}{x} = 0 $$ $$ \lim_{x \rightarrow +∞ } \frac{f(x)}{x} - m = 0 $$ $$ \lim_{x \rightarrow +∞ } \frac{f(x)}{x} = m $$

Si la pendiente m existe y es distinta de cero, a continuación se calcula la ordenada q:

$$ q= \lim_{x \rightarrow ±∞ } f(x) - mx \ne ∞ $$

Demostración. Si $$ \lim_{x \rightarrow +∞ } f(x) - (mx+q) = 0 $$ entonces: $$ \lim_{x \rightarrow +∞ } f(x) - mx - q = 0 $$ $$ \lim_{x \rightarrow +∞ } f(x) - mx = q $$

Si q existe y es finita, la función tiene una asíntota oblicua y = mx + q cuando x → +∞. En caso contrario, no.

El mismo procedimiento sirve para estudiar la existencia de una asíntota oblicua cuando x → -∞.

Ejemplo

Examinemos si la siguiente función presenta una asíntota oblicua:

$$ f(x) = \frac{x^2}{x-1} $$

Comprobamos primero que el límite cuando x → ∞ es infinito:

$$ \lim_{x \rightarrow ∞} \frac{x^2}{x-1} = ∞ $$

Nota. Este límite corresponde a una indeterminación ∞/∞, que puede resolverse con la Regla de L'Hôpital.

A continuación verificamos si la pendiente m es distinta de cero:

$$ m = \lim_{x \rightarrow ∞} \frac{ \frac{x^2}{x-1} }{x} $$

$$ m = \lim_{x \rightarrow ∞} \frac{x^2}{x(x-1)} $$

$$ m = \lim_{x \rightarrow ∞} \frac{x}{(x-1)} = 1 $$

Como m = 1 es finita y distinta de cero, calculamos ahora la ordenada q:

$$ q = \lim_{x \rightarrow ∞} \frac{x^2}{x-1} - mx $$

Con m = 1:

$$ q = \lim_{x \rightarrow ∞} \frac{x^2}{x-1} - x $$

$$ q = \lim_{x \rightarrow ∞} \frac{x^2-x^2+x}{x-1} $$

$$ q = \lim_{x \rightarrow ∞} \frac{x}{x-1} = 1 $$

Por lo tanto, la función posee una asíntota oblicua con pendiente m = 1 y ordenada q = 1:

Asíntotas oblicuas en funciones racionales

Una función racional $ f(x)=\frac{A(x)}{B(x)} $ presenta una única asíntota oblicua cuando el grado $ n $ del polinomio numerador $ A(x) $ es exactamente una unidad mayor que el grado $ m $ del polinomio denominador $ B(x) $. $$ n = m+1 $$

Ejemplo

Consideremos la función racional:

\[ f(x) = \frac{x^3 + 2x^2 - 1}{x^2 - 1} \]

El numerador es de grado 3 y el denominador de grado 2.

$$ n=3 $$

$$ m=2 $$

Como la diferencia es $ 3-2=1 $, la función tiene una asíntota oblicua.

Para determinarla, realizamos la división de polinomios:

$$ \begin{array}{cccc|cc} x^3 & +2x^2 & 0x & -1   & x^2 & -1  \\  -x^3 &  & +x &   & x +2 \\ \hline  & 2x^2 & +x & \\  & -2x^2 & & +2 \\ \hline  &  & -x & +1 \end{array} $$

El resultado es:

\( Q(x) = x+2 \) (cociente)

\( R(x) = -x+1 \) (resto)

Esto permite escribir la función como:

$$ \frac{A(x)}{B(x)} = Q(x) + \frac{ R(x) }{B(x)} $$

Explicación. La división de polinomios cumple $$ A(x) = Q(x)\cdot B(x) + R(x) $$ Al dividir ambos miembros entre $ B(x) $, se obtiene $$ \frac{A(x)}{B(x)} = Q(x) + \frac{R(x)}{B(x)} $$

Sustituyendo en nuestro caso:

$$ \frac{x^3+2x^2-1}{x^2-1} = (x+2) + \frac{-x+1}{x^2-1} $$

Cuando $ x \to \infty $, el término del resto se hace cada vez más pequeño:

$$ \lim_{x \to \infty} \frac{-x+1}{x^2-1} = 0 $$

Por tanto, para valores grandes de $ x $, la función se comporta prácticamente como una recta.

En concreto:

$$ f(x) \approx x + 2 $$

Esto significa que la gráfica se aproxima a la recta:

$$ y = x + 2 $$

Esta recta es la asíntota oblicua de la función.

La idea esencial es que, a medida que $ x $ crece, el término lineal domina el comportamiento de la función, mientras que el resto pierde relevancia. Por eso, la gráfica se acerca cada vez más a la recta \( y = x + 2 \).

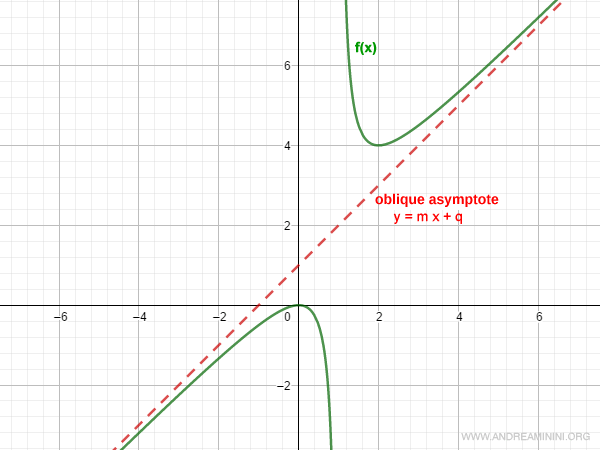
Y así sucesivamente.