Funciones Matemáticas
¿Qué es una función?
Una función es un tipo particular de relación entre dos conjuntos, A y B, en la cual a cada elemento de A (el dominio) le corresponde uno y solo uno de B (el codominio). $$ f:A \rightarrow B $$
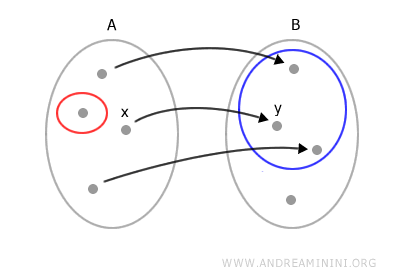
La expresión "uno y solo uno" significa que cada elemento de A se empareja con un único elemento de B. A continuación se muestra un ejemplo de función.
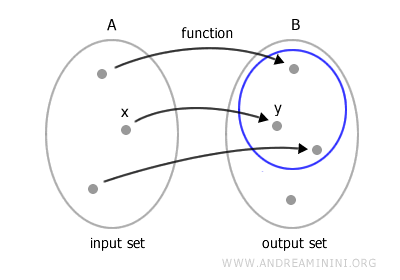
El conjunto A se denomina dominio, o también conjunto de definición, de la función.
Para cualquier elemento x en A, existe un único elemento y en B, llamado imagen de x bajo la función f.
$$ y = f(x) $$
Esta expresión se lee como "y es igual a f de x".
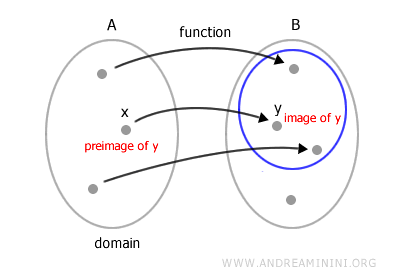
De manera recíproca, el elemento x recibe el nombre de preimagen de y.
Nota. Como cada entrada se asocia con un único resultado, la función y = f(x) también se denomina aplicación, y decimos que "f lleva x en y". Por ejemplo, la función f = x2 toma cualquier número real y devuelve su cuadrado. Si x = 2, entonces y = 22 = 4.
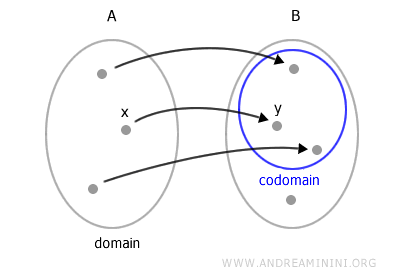
No es necesario que todos los elementos y de B sean imagen de algún x en A.
El subconjunto C ⊆ B que contiene todos los valores y = f(x) con x en A se denomina imagen de la función.
Nota. Dado que el valor de salida y depende de la entrada x, y se llama variable dependiente, mientras que x es la variable independiente.
Las funciones suelen representarse con letras minúsculas como f, g o h.
$$ f:A \rightarrow B $$
De forma equivalente, para todo x ∈ A y y ∈ B, podemos escribir
$$ f:x \longmapsto y $$
Una función f también se describe como una correspondencia unívoca, porque cada elemento del dominio se asocia con un único elemento del codominio.
¿Cuándo una relación no es una función? Una relación no es función si un mismo elemento de A se asocia con más de un elemento de B.
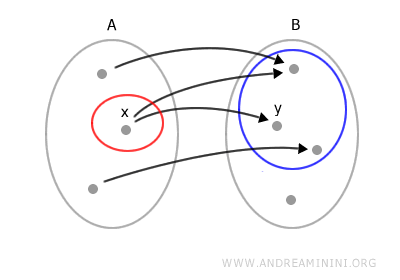
Asimismo, una relación no es función si al menos un elemento de A no se asocia con ningún elemento de B.
Las funciones también pueden depender de dos o más variables independientes.
$$ y = f(x_1, x_2, ...) $$
En este caso, las variables independientes dentro de los paréntesis - x1, x2, etc. - se denominan argumentos de la función.
Aun con varias entradas, una función siempre produce un único resultado: una sola variable dependiente.
Dominio de una Función
El dominio de una función es el conjunto de todos los valores permitidos de la variable independiente x, es decir, todos aquellos para los que la función está definida.
Por ejemplo, la siguiente función real está definida para todos los números reales excepto el cero:
$$ \frac{1}{x} $$
La división por cero no está definida en matemáticas.
Por lo tanto, el dominio de esta función es el conjunto de todos los números reales excepto el cero:
$$ \mathbb{R}- \{0 \} $$
En otras palabras, es el conjunto de números reales R, excluyendo el cero.
Funciones Explícitas e Implícitas
Una función matemática puede expresarse en forma explícita o implícita.
- Forma explícita
En forma explícita, la función se escribe como y = f(x). Por ejemplo: $$ y = x + 1 $$ - Forma implícita
En forma implícita, la función se expresa mediante una ecuación que involucra ambas variables, normalmente escrita como F(x, y) = 0. Por ejemplo: $$ y - x - 1 = 0 $$
Una función también puede representarse como un conjunto de pares ordenados (x, y), donde x ∈ A y y ∈ B, de manera que cada valor de x aparezca una única vez.
$$ f:A \rightarrow B $$
Dicho de otro modo, para cada a ∈ A, la función f asigna exactamente un b ∈ B.
$$ b = f(a) $$
En el par ordenado (a, b), el elemento a se denomina entrada o argumento de f, y b es la salida o imagen de a bajo f (también llamado valor de f en a).
$$ (a,b)_f = (a,f(a)) $$
Cada par (a, b) puede representarse en el plano cartesiano, lo que se conoce como la representación cartesiana de la función.
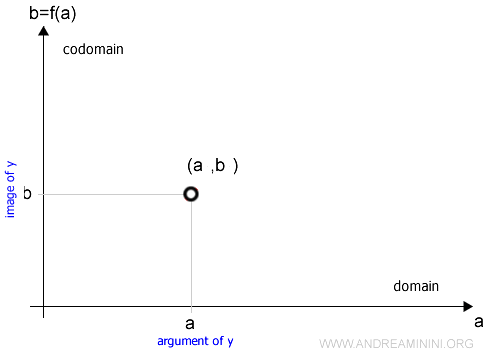
El conjunto F de todos esos pares ordenados definidos por la función f se denomina gráfica de la función.
Dicha gráfica es un subconjunto del producto cartesiano A × B.
$$ \{(a, f(a)) \mid a \in A \} \subseteq A \times B $$
Nota. No todo subconjunto de A × B define una función. Para que un conjunto de pares ordenados defina una función, cada entrada a ∈ A debe aparecer exactamente una vez. Otros subconjuntos de A × B pueden representar relaciones, pero no necesariamente funciones.
Un Ejemplo Concreto de Función
Ejemplo 1
Consideremos la función f: ℝ → ℝ definida por:
$$ f(x) = x^2 + 1 $$
Para cada número real x existe un valor correspondiente f(x):
$$ f(0) = 0^2 + 1 = 1 \\ f(1) = 1^2 + 1 = 2 \\ f(2) = 2^2 + 1 = 5 \\ \vdots $$
Ejemplo 2
Una función también puede establecer correspondencias entre conjuntos de distinta naturaleza.
En este caso, el dominio es el conjunto de los números reales, mientras que el codominio es el conjunto de los números enteros:
$$ f: \mathbb{R} \rightarrow \mathbb{Z} $$
Por ejemplo, consideremos la función f(x) = ⌊x⌋ (función parte entera):
$$ f(2.2) = \lfloor 2.2 \rfloor = 2 \\ f(3.4) = \lfloor 3.4 \rfloor = 3 \\ f(3.5) = \lfloor 3.5 \rfloor = 3 \\ \vdots $$
Gráfica de una Función
Cada valor de entrada a del dominio aparece una sola vez en los pares ordenados (a, b). En cambio, un mismo valor de salida b puede repetirse varias veces.
De este modo, la gráfica de la función f: A → B puede representarse mediante un diagrama cartesiano.
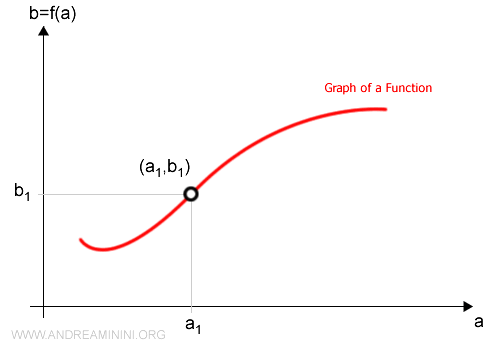
El eje horizontal (eje x) representa los valores de entrada a ∈ A (el dominio), mientras que el eje vertical (eje y) representa los valores de salida b ∈ B (el codominio).
Cada punto del diagrama pertenece al producto cartesiano A × B, pero solo los puntos situados sobre la curva roja forman parte de la gráfica de la función.
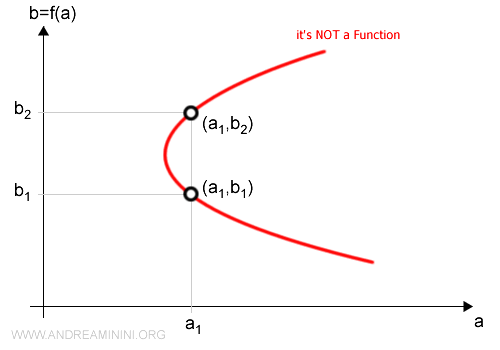
Nota. La gráfica de una función es siempre un subconjunto de A × B, aunque no todo subconjunto de A × B corresponde a una función. Por ejemplo, la siguiente gráfica no es válida porque algunos valores de entrada a aparecen más de una vez en los pares ordenados (a, b).
Valores Positivos y Negativos de una Función
En los intervalos donde la función cumple y = f(x) > 0, se dice que la función es positiva.
En los intervalos donde y = f(x) < 0, la función se considera negativa.
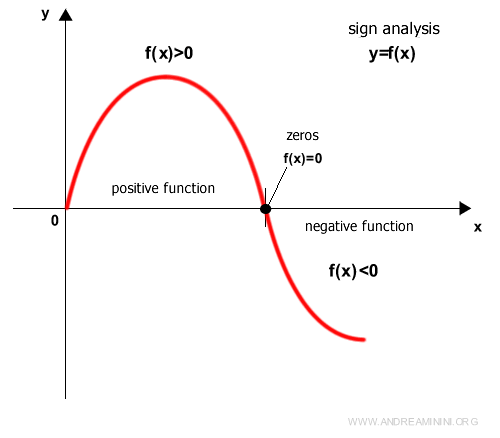
Los puntos donde f(x) = 0 se denominan ceros o raíces de la función.
Para determinar el signo de una función se recurre a un análisis de signos.
Nota. Otras características de una función - como crecimiento y decrecimiento, concavidad, convexidad, extremos y puntos de inflexión - se estudian mediante un análisis más profundo de la función utilizando herramientas del cálculo.
Clasificación de las funciones
En matemáticas, las funciones se clasifican atendiendo a las operaciones que intervienen en la expresión f(x). Esta clasificación permite comprender mejor su estructura y facilita el estudio de sus propiedades.
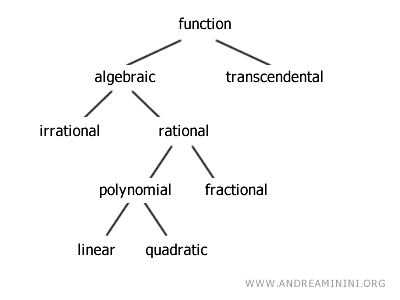
Las funciones algebraicas son aquellas que se obtienen combinando las cuatro operaciones aritméticas fundamentales (suma, resta, multiplicación y división), junto con potencias y o raíces. Se trata de las funciones más habituales en los primeros cursos de matemáticas.
En contraste, las funciones que no pueden expresarse únicamente mediante estas operaciones se denominan funciones trascendentes. Son ejemplos típicos aquellas en las que la variable independiente x aparece como argumento de una función trigonométrica, logarítmica o exponencial.
Ejemplo. Un ejemplo de función algebraica es $$ y=2x^3-x $$ Un ejemplo de función trascendente es $$ y=2x^3- \sin(x) $$ Basta la presencia de un solo término trascendente para que toda la función se clasifique como trascendente.
Las funciones algebraicas se subdividen a su vez en irracionales y racionales, según que la variable x aparezca bajo un radical o únicamente con exponentes enteros.
Ejemplo. Un ejemplo de función algebraica irracional es $$ y=2x^3-\sqrt{x} $$ Un ejemplo de función algebraica racional es $$ y=2x^3- x $$
Dentro de las funciones racionales, se distingue además entre polinómicas y fraccionarias, dependiendo de si la expresión está formada por un solo polinomio o por el cociente de dos polinomios.
Ejemplo. Un ejemplo de función polinómica es $$ y=2x^3-x $$ Un ejemplo de función racional fraccionaria es $$ y= \frac{2x^3-2}{x^2+2x-5} $$
Las funciones polinómicas reciben nombres específicos según el grado del polinomio. Se denominan lineales cuando el grado es uno y cuadráticas cuando el grado es dos.
Ejemplo. Un ejemplo de función lineal es $$ y=2x-1 $$ Un ejemplo de función cuadrática es $$ y= 2x^2 -1 $$
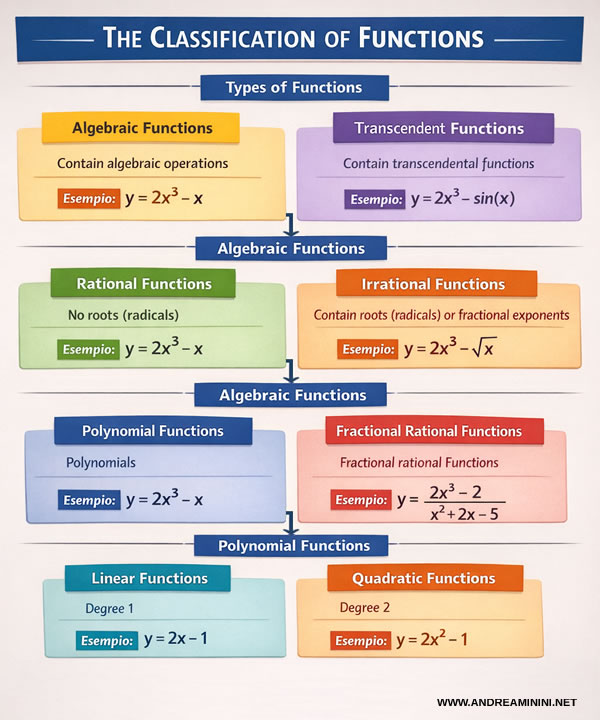
En síntesis, el esquema que se muestra a continuación ofrece una visión clara y ordenada de los principales tipos de funciones y de los criterios utilizados para su clasificación.
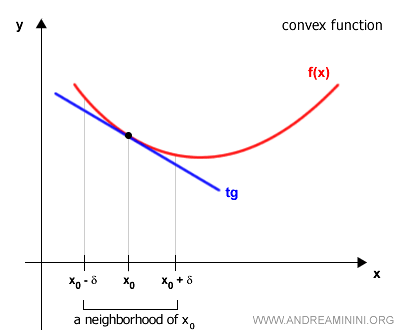
Funciones Cóncavas y Convexas
En un intervalo [a, b], una función puede describirse como:
- Convexa
si su gráfica se encuentra por encima de la tangente en todo punto de la curva.
- Cóncava
si su gráfica se sitúa por debajo de la tangente en cada punto.
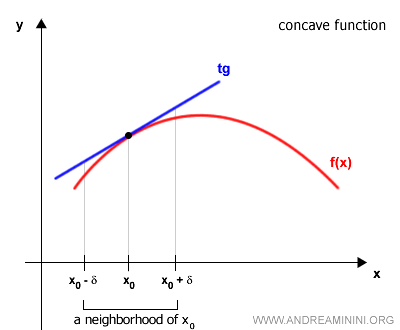
Una función puede ser cóncava o convexa en todo su dominio o únicamente en ciertos intervalos.
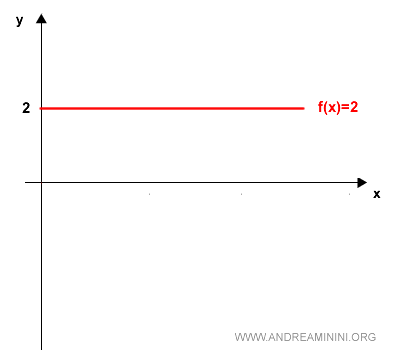
Nota. Además de las funciones cóncavas y convexas, existen funciones constantes que no son ni cóncavas ni convexas.
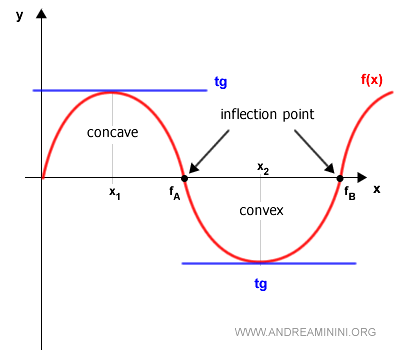
Asimismo, en ciertos puntos críticos - llamados puntos de inflexión - una función puede cambiar de concavidad, siendo cóncava a un lado y convexa al otro (o viceversa).
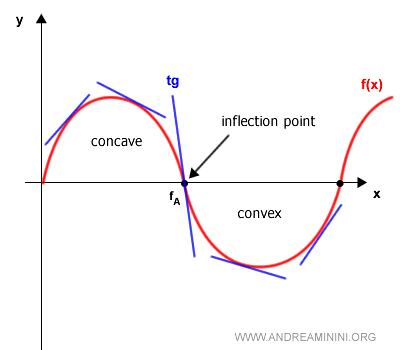
Imagen y Preimagen
La imagen de un conjunto A (el dominio) mediante una función f es el conjunto correspondiente B (el codominio):
$$ B = f(A) $$
La preimagen (o imagen inversa) de B por f es el conjunto original A. Se corresponde con la relación inversa f-1, que asocia cada elemento de B con uno y solo un elemento de A:
$$ A = f^{-1}(B) $$
Nota. Toda relación admite una relación inversa. Sin embargo, no todas las funciones tienen función inversa f-1. En muchos casos, la relación inversa no define una función, ya que un mismo valor del codominio puede corresponder a varios valores del dominio. Por ejemplo, la función f(x) = x2 no tiene inversa como función, porque y = 4 corresponde tanto a x = 2 como a x = -2 dentro del dominio de f.
Funciones Inyectivas, Sobreyectivas y Biyectivas
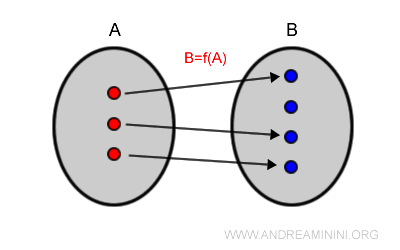
Una función es inyectiva (o uno a uno) si cada elemento del dominio se asocia con un único valor del codominio: $$ x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) $$
Ejemplo 1
La función y = x + 2 es inyectiva, ya que ningún par de valores distintos de x produce el mismo resultado y.
Por ejemplo, x = 2 y x = -2 se corresponden con y = 4 y y = 0, respectivamente.
Ejemplo 2
La función y = x2 no es inyectiva, pues distintos valores de x generan el mismo resultado: x = 2 y x = -2 dan ambos y = 4.
Una función es sobreyectiva (o sobre) si cada elemento del codominio es imagen de al menos un elemento del dominio: $$ \forall \ b \in B, \:\: \exists \ a \in A \text{ tal que } f(a) = b $$ 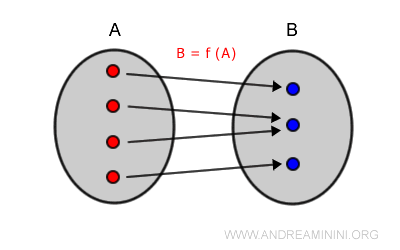
Ejemplo 1
La función y = x2 no es sobreyectiva cuando el codominio es ℝ, ya que los números negativos no tienen raíces cuadradas reales y por tanto no poseen preimagen.
Ejemplo 2
La función y = x + 1 sí es sobreyectiva en ℝ, puesto que para todo número real y existe un x = y - 1 en el dominio.
Una función es biyectiva (o correspondencia uno a uno) si es simultáneamente inyectiva y sobreyectiva.
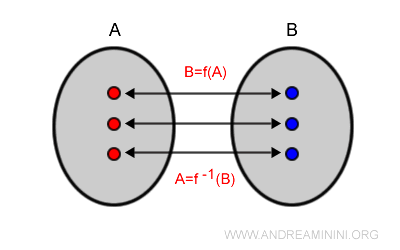
Solo las funciones biyectivas y = f(x) admiten siempre una función inversa x = f-1(y).
En este caso, la composición con su inversa devuelve el valor original de entrada. Esta se denomina función identidad:
$$ f^{-1}(f(x)) = x $$
Nota. Una función se denomina función identidad si cumple f(x) = x para todo x en su dominio.
Funciones Compuestas
Dadas dos funciones f: A → B y g: B → C, la composición de f con g se denota: $$ f \circ g : A \rightarrow C $$ o de manera equivalente: $$ F = f[g(x)] $$ Aquí, f es la función exterior y g la función interior.
Ejemplo
Sean f(x) y g(x) las siguientes funciones:
$$ f(x) = x + 1 $$
$$ g(x) = 2x + 3 $$
La función compuesta g ∘ f resulta ser:
$$ g(f(x)) = g(x + 1) = 2(x + 1) + 3 = 2x + 5 $$
Y así sucesivamente.