Funciones lineales
¿Qué es una función lineal?
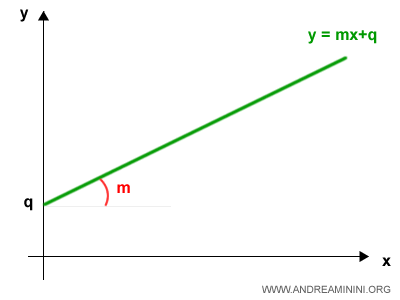
Se denomina función lineal (o función afín) a toda función que puede expresarse en la forma: $$ y = m \cdot x + q $$ donde $ m $ y $ q $ son números reales.
Las funciones lineales se representan en el plano cartesiano mediante rectas.
El parámetro $ m $ recibe el nombre de pendiente, pues determina la inclinación de la recta.
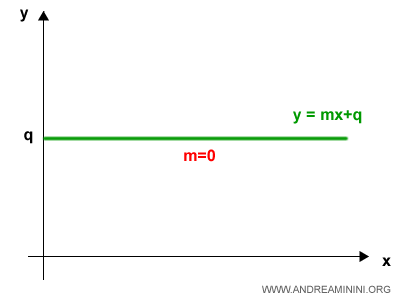
En el caso particular en que $ m = 0 $, la función se denomina función constante, y su gráfica corresponde a una recta horizontal paralela al eje x.
Observación. Todas las funciones lineales son monótonas: resultan crecientes o decrecientes. Cuando la pendiente es distinta de cero ($m \ne 0$), son además estrictamente monótonas, lo que implica que son biyectivas y, por tanto, invertibles: $$ y = m x + q $$ $$ x = \frac{y - q}{m} $$
Un ejemplo práctico
Consideremos la siguiente función lineal:
$$ f(x) = 2x + 3 $$
La representación gráfica de esta función es una recta en el plano.
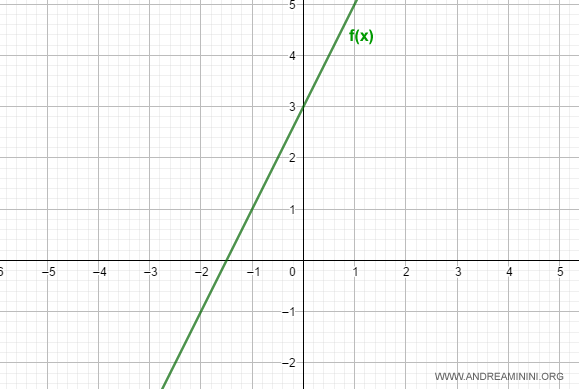
La pendiente de la recta es $ m = 2 $, lo que determina su inclinación.
El parámetro $ q = 3 $ fija la ordenada en el origen, es decir, el punto donde la recta corta al eje y.
Y así sucesivamente.