Función inversa
¿Qué es una función inversa?
Dada una función $y = f(x)$, la función inversa $f^{-1}$ invierte esta correspondencia, asignando a cada elemento del codominio $Y$ un único elemento del dominio $X$.
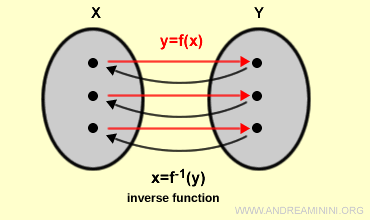
Una función de $X$ en $Y$ se dice invertible si existe una función inversa de $Y$ en $X$.
Si $f$ es una función biyectiva de $X$ en $Y$, entonces:
$$ f: X \rightarrow Y $$
su inversa $f^{-1}$ también es biyectiva y se define como:
$$ f^{-1}: Y \rightarrow X $$
de modo que para todo $y \in Y$ existe un único $x \in X$ tal que $y = f(x)$.
Nota. La notación $f^{-1}$ indica la inversa de la función $f$ - no significa $1/f$.
No todas las funciones poseen inversa. Aquellas que sí la tienen se denominan funciones invertibles.
Toda función biyectiva - es decir, inyectiva y sobreyectiva al mismo tiempo - es necesariamente invertible.
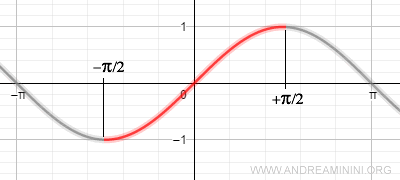
Nota. Algunas funciones no son invertibles en todo su dominio, pero lo son si se restringen a un subdominio adecuado. Por ejemplo, la función seno no es biyectiva - y, por tanto, no es invertible - en toda la recta real. Sin embargo, restringida al intervalo $(-\pi/2, \pi/2)$ se convierte en biyectiva, y su inversa recibe el nombre de función arcoseno.
Un ejemplo práctico
Ejemplo 1
Consideremos la función $f(x) = x + 1$ y los conjuntos:
$$ X = \{1, 2, 3\}, \quad Y = \{2, 3, 4\} $$
La función $f$ define una relación $R$, subconjunto del producto cartesiano $X \times Y$:
$$ R = \{(1, 2), (2, 3), (3, 4)\} $$
En este caso, cada elemento de $X$ se corresponde de manera unívoca con un elemento de $Y$:
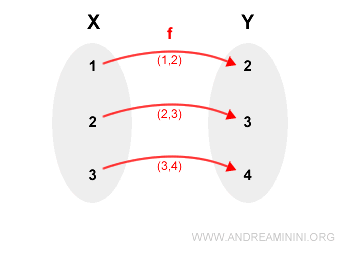
Nota. La relación $f$ es una función porque en los pares ordenados ningún primer elemento aparece repetido.
La relación inversa $R^{-1}$ es:
$$ R^{-1} = \{(2, 1), (3, 2), (4, 3)\} $$
Esta inversa también constituye una función, ya que cada primer elemento aparece una sola vez:
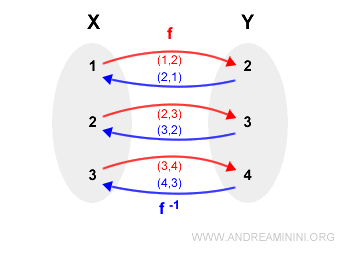
Así, $f^{-1}$ es la función inversa de $f$, y $f$ resulta ser una función invertible.
Ejemplo 2
Sea ahora:
$$ X = \{-1, 0, 1\}, \quad Y = \{-1, 0, 1\} $$
Consideremos la relación dada por $y = x^2$, que produce:
$$ R = \{(-1, 1), (0, 0), (1, 1)\} $$
Se trata de una función válida, pues ningún valor de $x$ se repite:
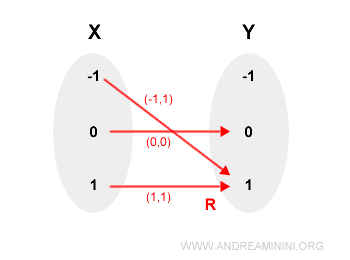
En cambio, la relación inversa $R^{-1}$ es:
$$ R^{-1} = \{(1, -1), (0, 0), (1, 1)\} $$
Y esta no es una función, porque el valor 1 se asocia a dos imágenes distintas:
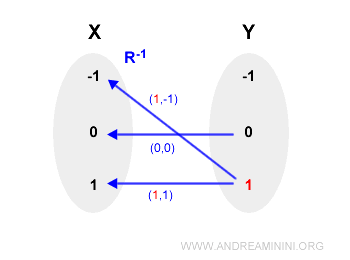
Por lo tanto, la inversa de $f(x) = x^2$ en el dominio $\{-1, 0, 1\}$ no es una función, y $f$ no es invertible en ese conjunto.
Ejemplo 3
Consideremos la función $y = 2x - 1$:
$$ y = 2x - 1 $$
Se trata de una función biyectiva y, en consecuencia, invertible.
Para obtener la inversa, despejamos $x$ en función de $y$:
$$ 2x = y + 1 $$
$$ x = \frac{y + 1}{2} $$
En la función inversa, $y$ se considera la variable independiente y $x$ pasa a ser la dependiente.
Si representamos gráficamente la función y su inversa en el mismo sistema de ejes, sus curvas aparecen simétricas.
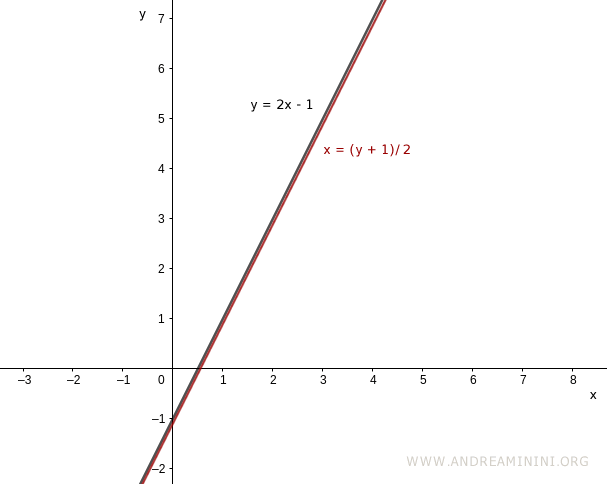
Para expresar la inversa en los ejes habituales, basta intercambiar $x$ e $y$:
$$ y = \frac{x + 1}{2} $$
Así se pueden representar ambas funciones en el mismo plano cartesiano:
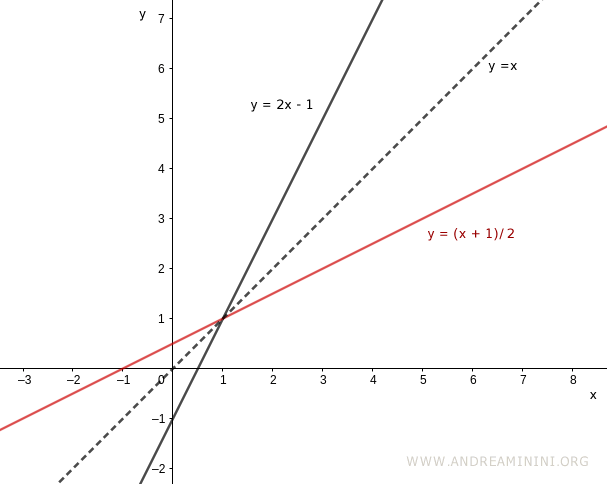
Las gráficas de $y = 2x - 1$ y de su inversa $y = \frac{x + 1}{2}$ son imágenes especulares respecto de la recta $y = x$, que biseca el primer y el tercer cuadrante.
Nota. Si un punto $P(x, y)$ pertenece a la gráfica de una función invertible, entonces el punto $P(y, x)$ pertenece a la gráfica de su inversa. Esta simetría se explica porque ambas son reflejos respecto de la recta $y = x$.
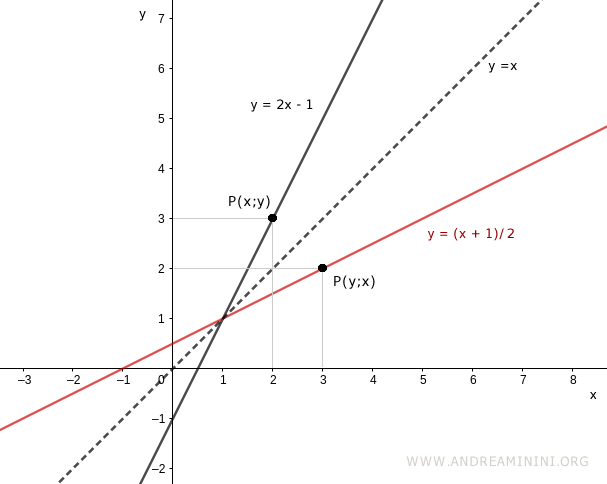
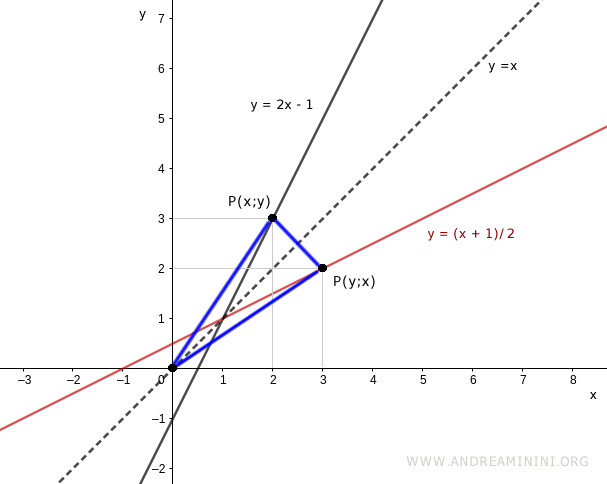
Si se trazan líneas desde cada punto al origen y se proyectan sobre los ejes, se obtienen dos triángulos rectángulos congruentes: una propiedad característica de las funciones inversas.
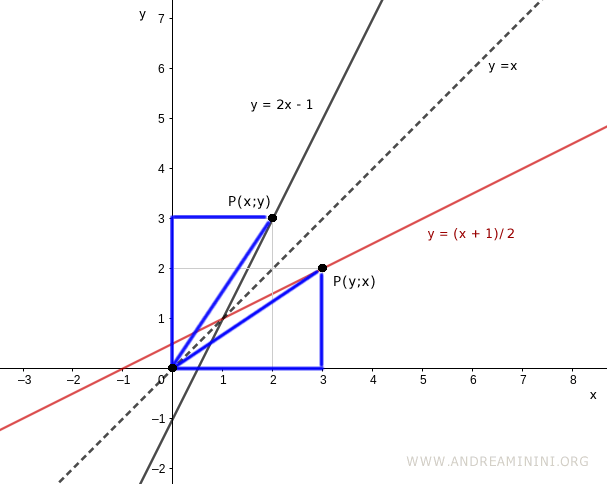
Al unir el origen con ambos puntos se forma además un triángulo isósceles, que pone de relieve la simetría geométrica.
Ejemplo 4
Consideremos ahora la función $y = x^2$, definida sobre el conjunto de los números reales $\mathbb{R}$:
$$ y = x^2 \quad \text{para todo } x \in \mathbb{R} $$
Esta función no es biyectiva y, por lo tanto, no es invertible en todo su dominio:
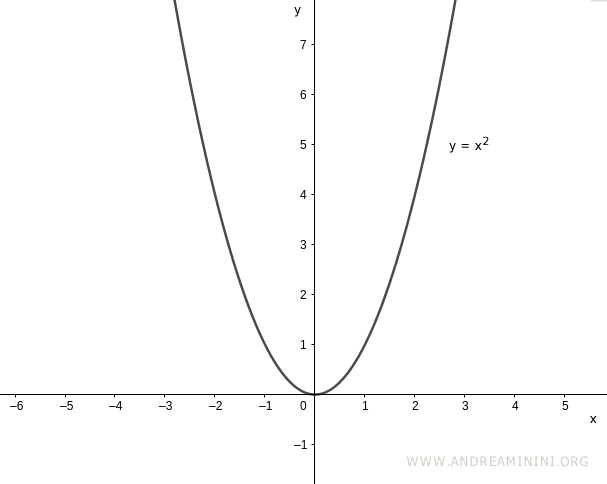
No obstante, si restringimos el dominio al conjunto de los números reales positivos $\mathbb{R}^+$, la función sí se vuelve biyectiva:
$$ y = x^2 \quad \text{para todo } x \in \mathbb{R}^+ $$
En el intervalo $(0, \infty)$, la función $y = x^2$ pasa a ser invertible:
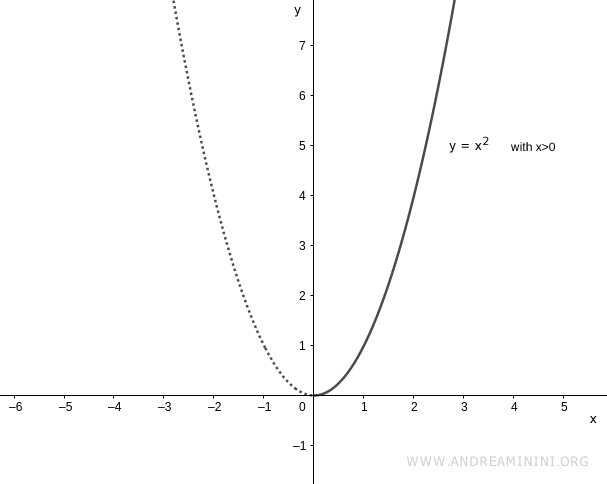
Para obtener la inversa, extraemos la raíz cuadrada de ambos lados y despejamos $x$:
$$ \sqrt{y} = \sqrt{x^2} $$
$$ x = \sqrt{y} $$
En forma estándar, tras intercambiar las variables, queda:
$$ y = \sqrt{x} $$
Las gráficas de la función original y de su inversa son simétricas respecto de la recta $y = x$:
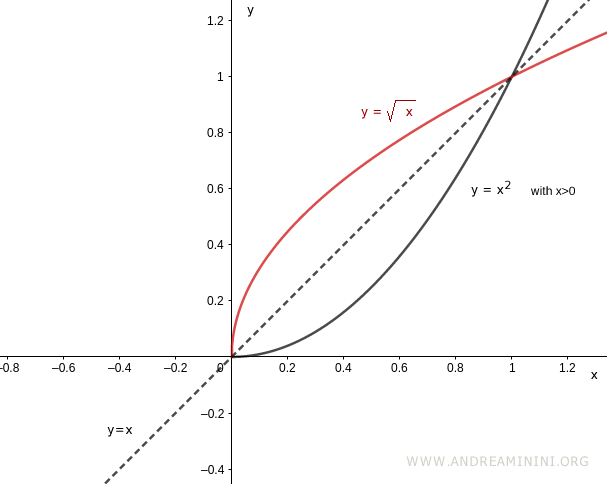
Nota. Este ejemplo ilustra que una función que no es invertible en todo su dominio puede llegar a serlo al restringirse a un intervalo en el que sí resulta biyectiva.
Las funciones biyectivas son invertibles
Si una función $f$ de $X$ en $Y$ es biyectiva, entonces también es invertible.
Una función es biyectiva (o correspondencia biunívoca) si cumple simultáneamente estas dos condiciones:
- Inyectiva: cada elemento del dominio $X$ se asocia con un elemento distinto del codominio $Y$.
- Sobreyectiva: todo elemento del codominio $Y$ es imagen de al menos un elemento del dominio $X$.
Demostración
Supongamos que $f(x)$ es una función biyectiva. Entonces se cumple:
$$ \text{dominio}(f) = \text{codominio}(f^{-1}) = X $$
$$ \text{codominio}(f) = \text{dominio}(f^{-1}) = Y $$
Si dos pares ordenados comparten la misma imagen:
$$ (x_1, y),\ (x_2, y) $$
Como $f$ es inyectiva, necesariamente:
$$ x_1 = x_2 $$
Y dado que $f$ es sobreyectiva, para cada $y \in Y$ existe un único $x \in X$ tal que:
$$ (x, y) $$
En consecuencia, la preimagen de $y$ es única y puede expresarse como:
$$ x = f^{-1}(y) $$
De este modo queda demostrado que toda función biyectiva admite inversa y, por tanto, es invertible.
Propiedades de las funciones inversas
Entre las propiedades más relevantes de las funciones inversas se encuentran:
- Si $f^{-1}$ es la inversa de $f$, entonces $f$ es a su vez la inversa de $f^{-1}$.
- Si $f^{-1}[f(x)] = x$, entonces también $f[f^{-1}(y)] = y$.
- Si $y = f(x)$ y $x = f^{-1}(y)$, ambas expresiones son equivalentes.
Cómo determinar la inversa de una función
La inversa $f^{-1}(x)$ de una función invertible $f(x)$ puede obtenerse mediante dos enfoques gráficos o a través de un procedimiento analítico.
Método 1: Reflexión respecto de la recta $y = x$
Se comienza trazando la gráfica de la función invertible $f(x)$. Por ejemplo, $y = \log x$:
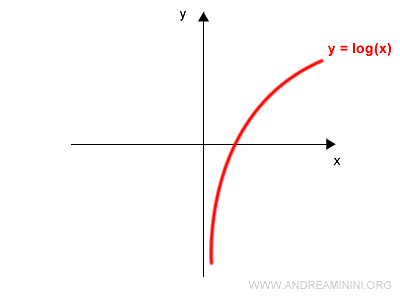
A continuación se dibuja la recta $y = x$, que biseca el primer y el tercer cuadrante formando un ángulo de 45° con los ejes:
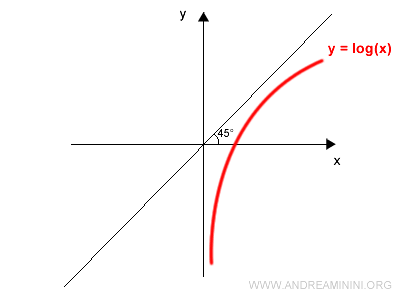
Se refleja la gráfica de $f(x)$ respecto de esa recta:
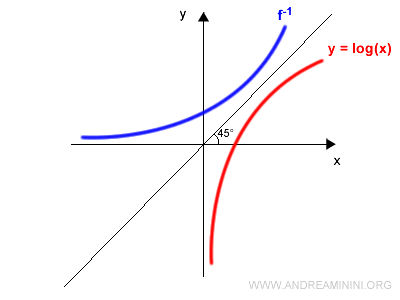
Después se elimina la gráfica original y se reetiquetan los ejes, intercambiando $x$ e $y$:
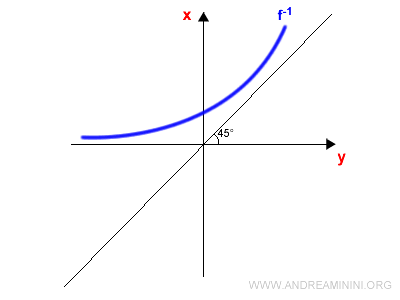
La curva obtenida corresponde a la función inversa $f^{-1}(x)$:
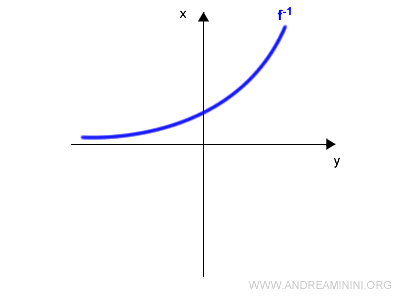
Método 2: Simetría rotacional
Representemos de nuevo una función invertible, como $y = \log x$:
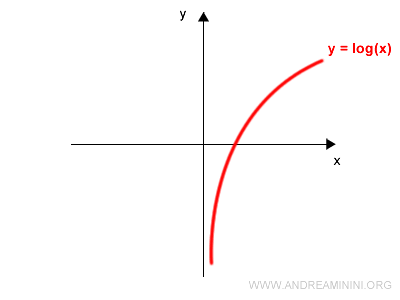
Rotamos el plano de coordenadas 90° en sentido antihorario: el eje $y$ queda a la izquierda y el eje $x$ apunta hacia arriba:
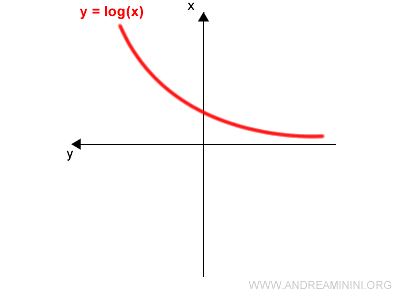
Posteriormente realizamos una rotación de 180° alrededor del eje vertical:
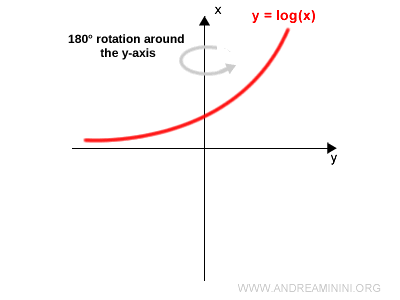
Nota. Esta última transformación equivale a reflejar la gráfica en un espejo vertical, obteniéndose el mismo resultado.
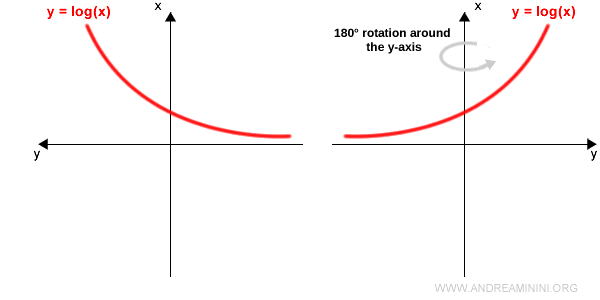
La curva resultante es la gráfica de la función inversa $f^{-1}(x)$:
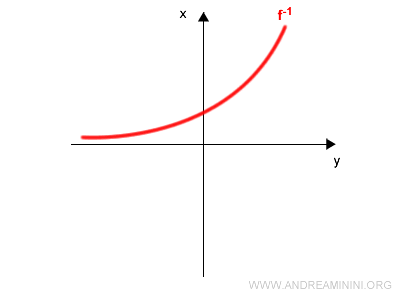
Método 3: Procedimiento analítico
Para calcular la inversa de una función $y = f(x)$ de forma analítica, basta con despejar $x$ en función de $y$.
Consideremos la función logarítmica:
$$ y = \log x $$
Su gráfica es la siguiente:
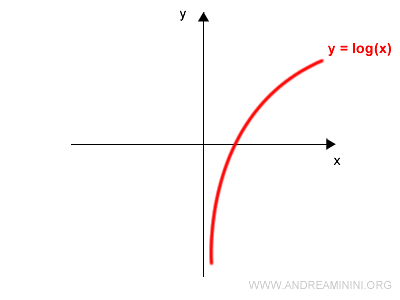
Aplicamos ahora la exponencial en ambos lados de la igualdad:
$$ e^y = e^{\log x} $$
Nota. Este paso es válido porque se efectúa la misma operación en ambos miembros de la ecuación.
Como $e^{\log x} = x$, obtenemos:
$$ e^y = x $$
Hemos expresado $x$ en función de $y$, de modo que la inversa queda:
$$ x = e^y $$
En su forma habitual, tras intercambiar $x$ e $y$, tenemos:
$$ y = e^x $$
La gráfica de la función exponencial inversa es la siguiente:
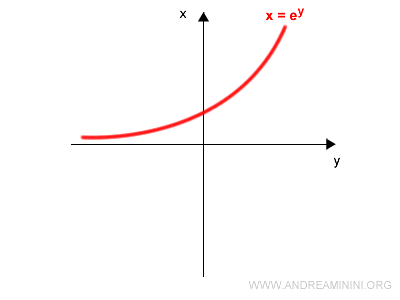
Nota. Este es el mismo resultado que se obtiene mediante el método gráfico explicado anteriormente en esta página.
Y así sucesivamente.
