Funciones de Lipschitz

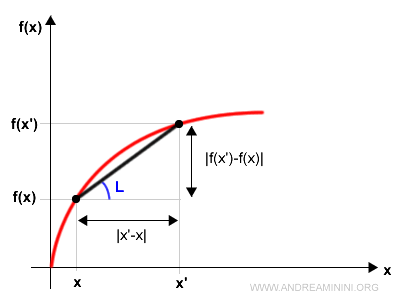
Se dice que una función f(x) es Lipschitz continua en un intervalo I ⊆ ℝ si existe una constante L tal que $$ |f(x) - f(x')| \le L |x - x'| $$ para todo x, x′ en I.

En este tipo de funciones, la variación de los valores de salida está controlada por una constante L, denominada constante de Lipschitz.

Esta condición es más exigente que la simple continuidad.

¿Qué implica esto? Desde un punto de vista geométrico, significa que, para cualesquiera dos puntos del intervalo, la pendiente de la secante que los une nunca supera el valor L.

El concepto fue introducido por el matemático alemán Rudolph Otto Sigismund Lipschitz.

Cómo reconocer una función de Lipschitz

Si f(x) es derivable en un intervalo I, entonces es Lipschitz continua en I con constante L si, y solo si, el valor absoluto de su derivada está acotado por L en todo el intervalo: $$ |f'(x)| \le L \quad \forall x \in I $$

En otras palabras, toda función derivable cuya derivada permanezca acotada en el intervalo resulta ser Lipschitz continua.

Demostración

Supongamos que para todo x en I se cumple $$ |f'(x)| \le L $$

Aplicando el Teorema del Valor Medio en [x, x′] obtenemos:

$$ |f(x) - f(x')| = |f'(x_0)(x - x')| \le L \cdot |x - x'| $$

lo que confirma la condición de Lipschitz.

Si ahora tomamos x′ = x + h:

$$ |f(x) - f(x + h)| \le L |h| $$

lo cual equivale, al invertir el orden, a:

$$ |f(x + h) - f(x)| \le L |h| $$

Dividiendo ambos lados entre |h| se obtiene:

$$ \frac{|f(x + h) - f(x)|}{|h|} \le L $$

Y al tomar el límite cuando h → 0 llegamos a la derivada:

$$ \lim_{h \to 0} \frac{|f(x + h) - f(x)|}{|h|} = |f'(x)| \le L $$

Nota. La condición de Lipschitz $$ |f(x) - f(x_0)| \le L |x - x_0| $$ también puede expresarse como $$ \frac{|f(x) - f(x_0)|}{|x - x_0|} \le L $$ Se trata del cociente incremental, que representa geométricamente la pendiente de la secante entre dos puntos.

Al hacer tender h → 0 obtenemos la derivada en x₀: $$ f'(x_0) = \lim_{h \to 0} \frac{|f(x_0 + h) - f(x_0)|}{|h|} \le L $$ Por tanto, si la derivada está acotada en todo el intervalo I, la función es Lipschitz continua.

Ejemplos

_{Ejemplo 1}

La función f(x) = x² es Lipschitz continua en el intervalo [0, 4] con L = 8.

$$ f(x) = x^2 $$

Como f es derivable, calculamos su derivada:

$$ f'(x) = 2x $$

Analizamos ahora la variación de la pendiente entre x₀ = 0 y x₁ = 4:

$$ |f'(x_1) - f'(x_0)| = |2(4) - 2(0)| = 8 $$

De ello se deduce que la derivada está acotada por 8 en [0, 4]:

$$ \frac{|f'(x_1) - f'(x_0)|}{|x_1 - x_0|} \le 8 $$

La gráfica lo ilustra claramente:

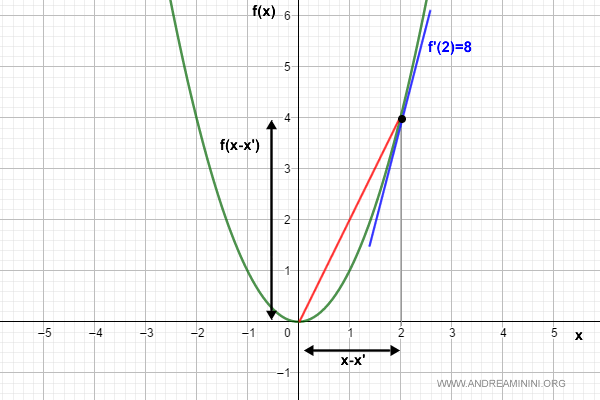
En todo el intervalo [0, 2], las tangentes a la curva presentan pendiente inferior a 8.

Por consiguiente, f(x) = x² es Lipschitz continua en [0, 4] con constante L = 8.

Ejemplo 2

La función seno es Lipschitz continua en ℝ con L = 1:

$$ f(x) = \sin x \quad \Rightarrow \quad f'(x) = \cos x $$

Como |cos x| ≤ 1 para todo x ∈ ℝ, la función satisface la condición de Lipschitz globalmente con L = 1.

La continuidad de Lipschitz implica continuidad uniforme

Toda función Lipschitz continua es también uniformemente continua en su dominio.

Dado un ε > 0, basta tomar δ = ε/L.

Así:

$$ \epsilon > 0 \quad \Rightarrow \quad \delta = \frac{\epsilon}{L} $$

De manera que, para cualesquiera x, x′ en I con |x - x′| < δ, se cumple:

$$ |f(x) - f(x')| < L |x - x'| < \epsilon $$

De este modo, la condición de continuidad uniforme queda automáticamente satisfecha.

Atención. La recíproca no es válida: una función uniformemente continua no tiene por qué ser Lipschitz.

Contraejemplo

La función f(x) = √x es uniformemente continua en [0, 1], pero no es Lipschitz continua en dicho intervalo.

En efecto, cuando x → 0, la derivada $$ f'(x) = \frac{1}{2\sqrt{x}} $$ tiende a infinito.

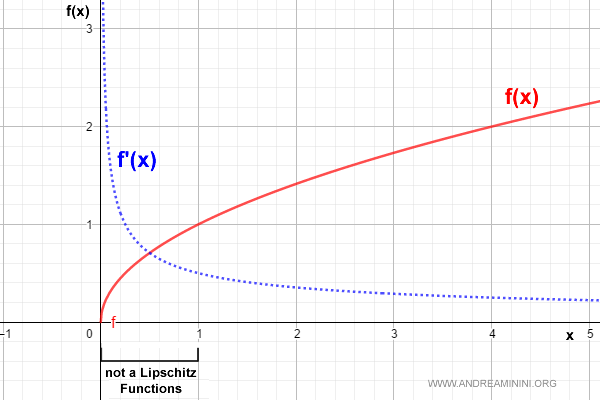
Por lo tanto, no existe ninguna constante L que cumpla la condición de Lipschitz en [0, 1].

Nota. No obstante, la misma función sí es Lipschitz continua en [1, ∞), donde su crecimiento puede acotarse mediante una constante adecuada L.

Y así sucesivamente.