Funciones continuas
Se dice que una función f(x) es continua en un punto x0 cuando el límite de la función al acercarse x a x0 coincide con el valor de la función en dicho punto: $$ \lim_{x \rightarrow x_0} f(x) = f(x_0) $$
La gráfica de una función continua es una curva suave y sin interrupciones, sin saltos ni discontinuidades.
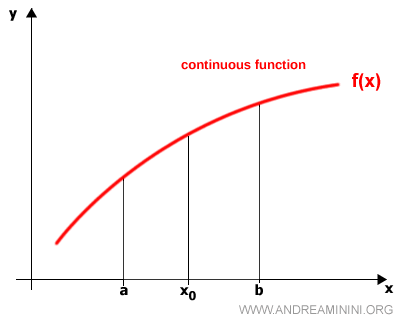
Continuidad en un intervalo
Una función es continua en el intervalo [a, b] si lo es en todos los puntos comprendidos en dicho intervalo:
$$ \lim_{x \rightarrow x_0} f(x) = f(x_0) \ \ \forall \ x_0 \in [a, b] $$
En los extremos del intervalo se consideran los límites laterales: el límite por la derecha en el extremo izquierdo a:
$$ \lim_{x \rightarrow a^+} f(x) = f(a) $$
y el límite por la izquierda en el extremo derecho b:
$$ \lim_{x \rightarrow b^-} f(x) = f(b) $$
Un ejemplo práctico
Consideremos la función:
$$ f(x) = x^2 $$
Comprobemos si la función es continua en x0 = 2:
$$ \lim_{x \rightarrow 2} x^2 = 4 $$
En x0 = 2, el valor de la función es:
$$ f(2) = 4 $$
Dado que el límite coincide con el valor de la función:
$$ \lim_{x \rightarrow 2} x^2 = f(2) $$
podemos concluir que la función x² es continua en x0 = 2.
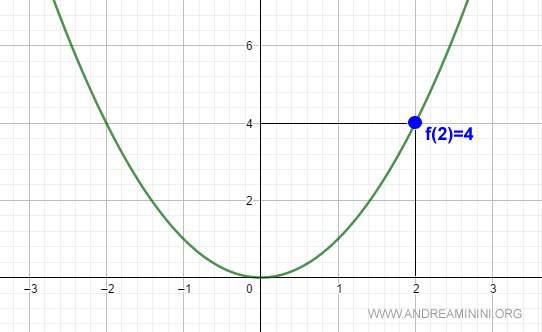
La misma conclusión se obtiene para cualquier otro punto x del dominio (−∞, ∞) de la función.
Y así sucesivamente.