Funciones biyectivas

¿Qué es una función biyectiva?

Una función $f(x)$ se denomina biyectiva (o correspondencia biunívoca) cuando es simultáneamente inyectiva y sobreyectiva.

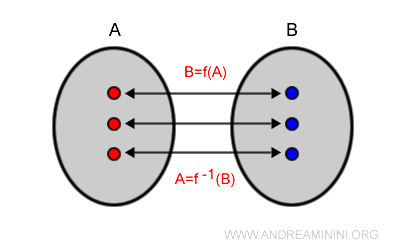
En otras palabras, cada elemento del dominio se asocia con un único elemento del codominio, y cada elemento del codominio es imagen de un único elemento del dominio.

$$ f: A \leftrightarrow B $$

Esto significa que:

• Cada $x \in A$ se corresponde con un único $y \in B$
• Cada $y \in B$ procede de un único $x \in A$

Nota. En una función biyectiva, todo elemento del dominio tiene una imagen única en el codominio y, recíprocamente, todo elemento del codominio posee una única preimagen en el dominio. Existe, por tanto, una correspondencia perfecta uno a uno entre los elementos de $A$ y de $B$.

Las funciones biyectivas también reciben el nombre de biyecciones o correspondencias biunívocas.

Un ejemplo práctico

La siguiente función es biyectiva porque cumple simultáneamente las condiciones de inyectividad y sobreyectividad:

$$ f(x) = x + 1 $$

Cada valor de entrada $x$ produce una salida distinta $y$, y cada valor de salida $y$ corresponde exactamente a una única entrada $x$.

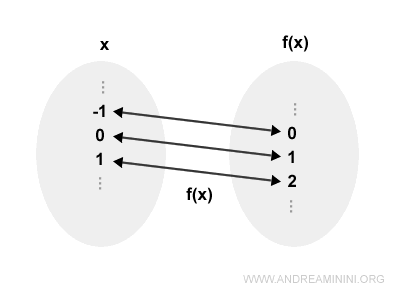
De este modo, dominio y codominio quedan en correspondencia biunívoca.

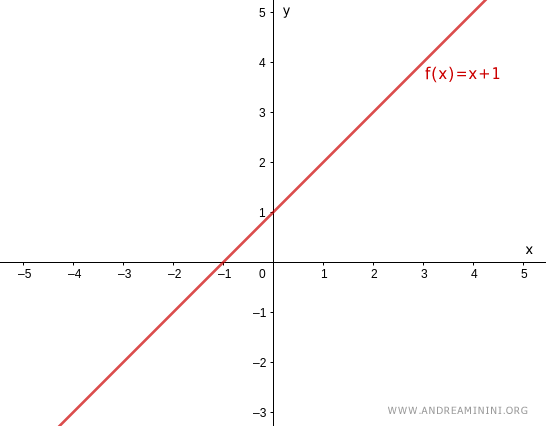
Propiedades fundamentales de las funciones biyectivas

Las funciones biyectivas presentan varias propiedades clave:

• Función inversa
  Toda función biyectiva es invertible; es decir, admite una función inversa: $$ x = f^{-1}(y) $$
• Función identidad
  La composición de una función biyectiva con su inversa da como resultado la función identidad: $$ x = f^{-1}(f(x)) $$

  Nota. Se denomina función identidad a aquella que cumple $f(x) = x$ para todo $x$ en su dominio.

Ejemplo

Consideremos la función:

$$ y = f(x) = x + 1 $$

Esta función es biyectiva y, por lo tanto, invertible. Su inversa es:

$$ x = f^{-1}(y) = y - 1 $$

La composición de la función con su inversa confirma la propiedad de identidad:

$$ x = f^{-1}(f(x)) $$

Dado que $f(x) = x + 1$, tenemos:

$$ x = f^{-1}(x + 1) $$

Y como $f^{-1}(y) = y - 1$, resulta:

$$ x = (x + 1) - 1 $$

$$ x = x $$

Tal como era de esperar, la composición devuelve la entrada original.