Funciones sinusoidales

Las funciones sinusoidales (o sinusoides ∿) se basan en las funciones de seno y coseno. $$ y = A \cdot \sin(\omega x + \phi) $$ $$ y = A \cdot \cos(\omega x + \phi) $$ donde A es la amplitud, ω (omega) la frecuencia angular (radianes por segundo) y φ (phi) el desfase o fase inicial. $$ A, \omega, \phi \in R $$

Ambas expresiones son equivalentes, ya que el coseno puede interpretarse como un seno desplazado en π/2 (90°).

$$ y = A \cdot \cos(\omega x + \phi) = A \cdot \sin(\omega x + \phi + \frac{\pi}{2}) $$

Al observar sus gráficas, la diferencia entre las ondas de seno y coseno resulta evidente.

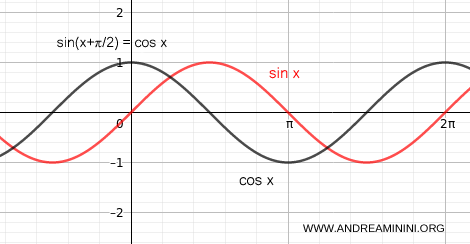
A la inversa, el seno puede verse como un coseno desplazado en -π/2 (-90°).

$$ y = A \cdot \sin(\omega x + \phi) = A \cdot \cos(\omega x + \phi - \frac{\pi}{2}) $$

Otra forma de expresar la relación entre seno y coseno es:

$$ \sin x = \cos(x - \frac{\pi}{2}) = \cos(\frac{\pi}{2} - x) $$

$$ \cos x = \sin(x + \frac{\pi}{2}) = \sin(\frac{\pi}{2} - x) $$

Por lo tanto, cualquier sinusoide puede escribirse como seno o como coseno, según cuál simplifique más el cálculo.

Nota: La elección entre seno y coseno depende del contexto. En muchos casos, optar por uno u otro facilita la manipulación algebraica.

¿Para qué sirven las ondas sinusoidales?

Las sinusoides son esenciales para describir gran cantidad de fenómenos físicos.

En física, por ejemplo, se utilizan para modelar el movimiento circular, el movimiento armónico simple, la corriente alterna o las señales sinusoidales en telecomunicaciones.

Nota: El análisis de Fourier permite descomponer cualquier señal periódica compleja en una suma de ondas sinusoidales.

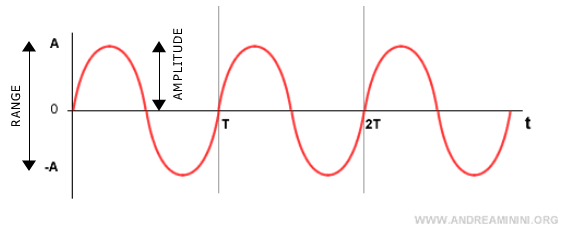
Amplitud

La amplitud |A| de una sinusoide determina la altura de la onda y su rango de variación, que va de -A a A.

Frecuencia angular (o pulsación)

La frecuencia angular (o pulsación) indica cuántos radianes recorre la onda por segundo y está relacionada con el período T de la sinusoide.

$$ \omega = \frac{2 \pi}{T} $$

Como la frecuencia f es el inverso del período T:

$$ f = \frac{1}{T} $$

también podemos escribir la frecuencia angular ω como:

$$ \omega = 2 \pi f $$

Cuantos más ciclos o radianes complete la onda en un segundo, mayor será su frecuencia angular ω (en rad/s).

Nota: El denominador 2π corresponde a los radianes de una vuelta completa, es decir, 360°.

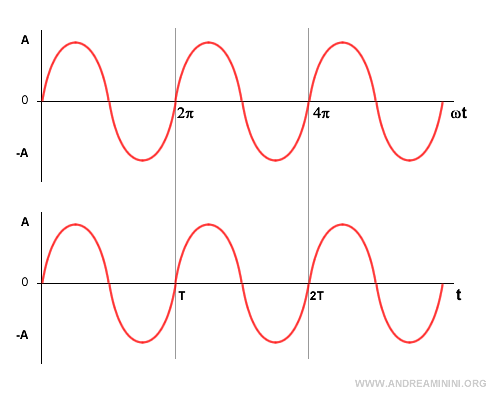
El argumento de la función sinusoidal ωt alcanza el valor 2π cuando t = 1.

$$ \omega t = 2 \pi $$

Esta relación se aprecia en los siguientes gráficos, donde se muestra claramente ωt = 2π.

Al aumentar la frecuencia angular, la onda completa más ciclos por segundo.

Por ejemplo, comparemos dos sinusoides:

La onda roja completa ω = 2 ciclos por segundo, mientras que la azul alcanza ω = 4 ciclos por segundo.

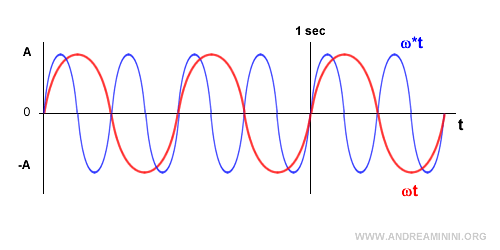
De este modo, la onda azul tiene una frecuencia angular mayor que la roja (ω*>ω). En un segundo, la azul recorre más radianes.

En este caso, la frecuencia angular de la onda azul es el doble de la de la roja (ω* = 2ω).

En conclusión, modificar la frecuencia angular ω altera el período T de la sinusoide.

$$ T = \frac{2 \pi}{\omega} $$

Período

Una sinusoide es periódica, es decir, se repite a intervalos regulares. $$ y(t) = y(t + T) $$

Por ejemplo, en los instantes t₁ y t₁ + T la onda sinusoidal toma el mismo valor: y(t₁) = y(t₁ + T) = -A.

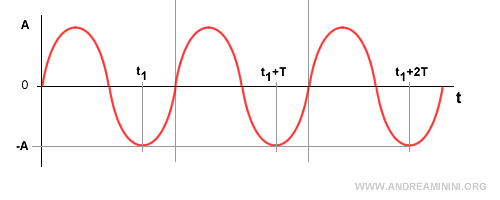
Esto se cumple para cualquier múltiplo de T: y(t₁) = y(t₁ + kT) = -A con k = 1, 2, 3, ...

$$ y(t) = y(t + kT) \ \ \ \ k=1,2,3,... $$

En general, considerando la frecuencia angular ω y el desfase φ, la forma periódica de una sinusoide puede expresarse como:

$$ y = \sin(x + kT) $$

$$ y = \sin (\omega (x + kT) + \phi) $$

Cualquier variación de la frecuencia angular ω modifica el período.

Dado que T = 2π/ω, un aumento de la frecuencia angular (Δω>0) acorta el período T.

$$ T = \frac{2 \pi}{\omega} $$

En cambio, una disminución de la frecuencia angular (Δω<0) alarga el período T.

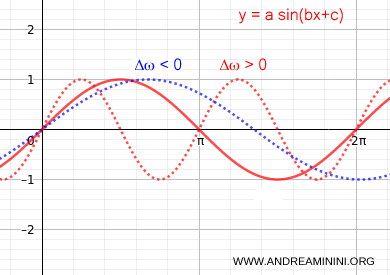
Nota: El desfase no afecta al período T de la sinusoide.

Estiramiento y compresión de sinusoides

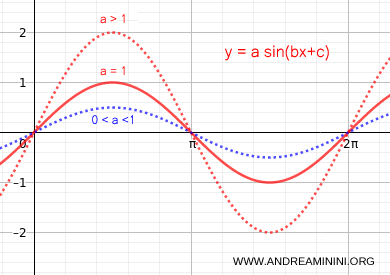
Cualquier sinusoide puede escribirse en la forma general: $$ y = a \sin (b \cdot x + c) $$

• El coeficiente a produce un estiramiento vertical (a>1) o una compresión vertical (0<a<1) de la amplitud de la onda.
  
• El coeficiente b provoca un estiramiento horizontal (0<b<1) o una compresión horizontal (b>1). Al modificar b (la frecuencia angular ω) se modifica el período (T) de la sinusoide.
  

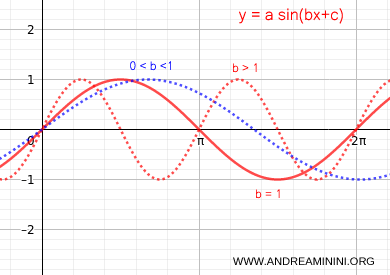
  Nota: En la práctica, si b>1 la frecuencia angular aumenta y la onda completa más radianes por segundo (más oscilaciones). Si 0<b<1, la frecuencia angular disminuye y la onda realiza menos oscilaciones por segundo.

• El coeficiente c produce un desplazamiento horizontal, moviendo la onda hacia atrás (c>0) o hacia adelante (c<0). Este desplazamiento se denomina desfase.
  

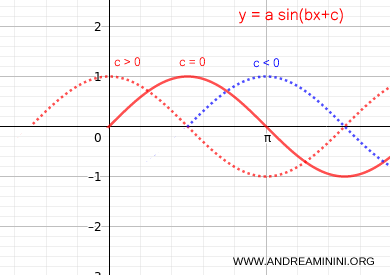
  Nota: En teoría de señales, desplazar la onda hacia atrás (c>0) se denomina adelanto, es decir, la sinusoide comienza antes del instante cero. Desplazarla hacia adelante (c<0) se denomina retardo, lo que significa que la onda comienza después del instante cero.

Y así sucesivamente.