Función arcocoseno
¿Qué es el arcocoseno?
El arcocoseno es la función trigonométrica inversa del coseno definida en el intervalo [0, π]. Se representa habitualmente con el símbolo arccos.
En ocasiones, también se escribe como cos-1, donde el -1 no indica una potencia, sino el símbolo matemático que denota la función inversa.
¿Cómo funciona el arcocoseno?
Dado un valor de coseno y, el arcocoseno determina el ángulo x (en radianes) cuyo coseno es precisamente ese valor.
Ejemplo
El coseno de un ángulo es 0,5:
$$ cos \ \alpha \ = 0.5 $$
¿Qué ángulo α produce este valor de coseno?
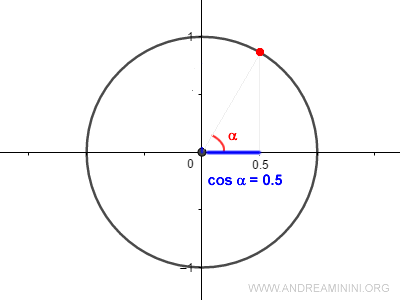
Para determinarlo, aplicamos la función arcocoseno:
$$ \alpha = arccos (0.5) = \frac{ \pi }{ 3 } \ rad $$
El arcocoseno localiza la longitud de arco x en la circunferencia unitaria que corresponde al valor de coseno dado.
Este arco se mide en radianes y tiene la misma magnitud que el ángulo x que define el coseno.
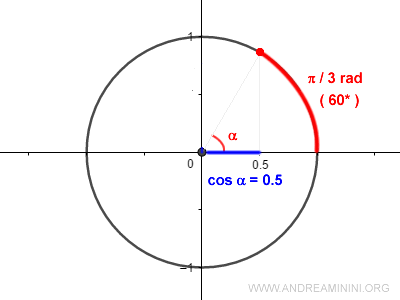
En este caso, el coseno es igual a 0,5 cuando el ángulo x es π/3 radianes (60°).
Explicación
La función coseno toma valores comprendidos entre -1 y +1.
Al ser periódica, un mismo valor de cos(x) puede corresponder a distintos ángulos x, como por ejemplo x1 y x2.
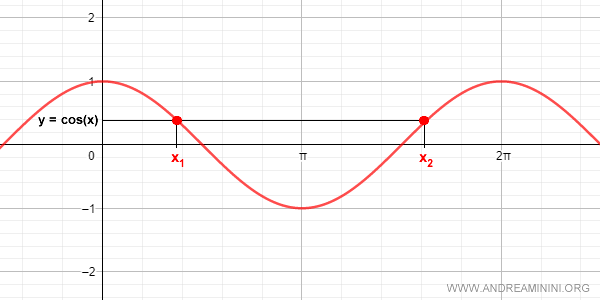
Por este motivo, no es posible definir una función inversa única para el coseno en todo su dominio, ya que no se cumple la condición de correspondencia biunívoca necesaria.
$$ f:x -> y $$
¿Cómo se construye la inversa del coseno?
La solución consiste en restringir el dominio de la función coseno a un intervalo en el que sea estrictamente decreciente o creciente, asegurando así la correspondencia uno a uno entre x e y.
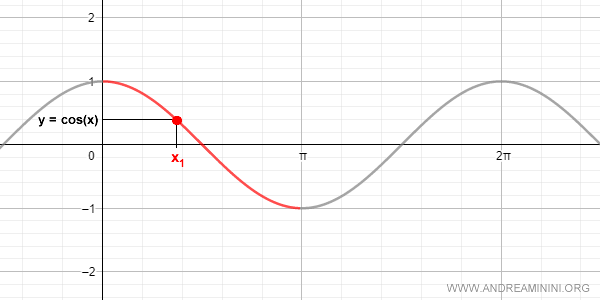
En el intervalo [0, π], existe una relación biunívoca entre los valores del coseno en [-1, +1] y los valores de x.
Esto permite definir la función inversa del coseno en dicho intervalo.
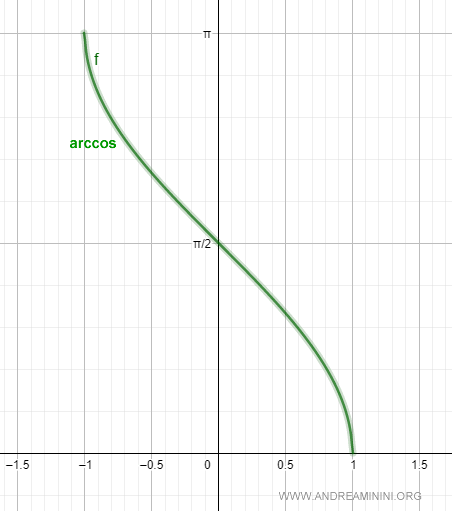
Esta función inversa se denomina arcocoseno:
$$ arccos(x) : [-1,1] → [0,π] $$
Se escribe comúnmente como arccos o acos.
A partir de un valor de coseno dado, la función arcocoseno calcula el ángulo x que lo genera dentro del intervalo [0, π].
Nota: El intervalo [0, π] no es el único rango en el que el coseno es invertible. También puede invertirse, por ejemplo, en [π, 2π] o en cualquier otro intervalo donde la función sea biyectiva.
Construcción de la gráfica de la función arcocoseno
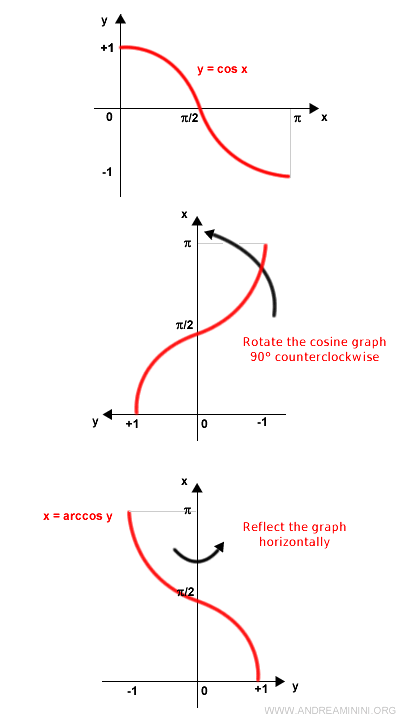
La gráfica del arcocoseno se obtiene a partir de la del coseno restringido al intervalo [0, π] siguiendo dos pasos sencillos:
- Girar la gráfica del coseno 90° en sentido antihorario.
- Reflejarla horizontalmente.
El resultado es la gráfica de la función arcocoseno.
Con el mismo procedimiento, es posible construir la gráfica del arcocoseno a partir de otros dominios reducidos.
Por ejemplo, [-π, 0] u otros intervalos en los que el coseno sea invertible.
Y así sucesivamente.