Teorema de la cuerda en trigonometría
La longitud de una cuerda en una circunferencia equivale al diámetro multiplicado por el seno de uno de los ángulos que subtiende dicha cuerda. $$ \overline{AB} = 2r \cdot \sin \alpha $$
En esta fórmula, r representa el radio de la circunferencia.
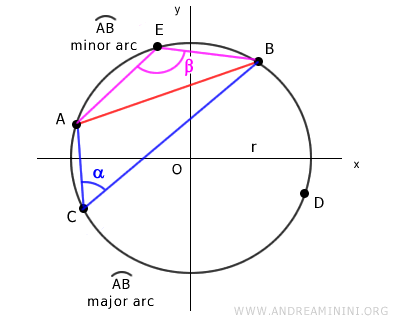
El ángulo alfa es el ángulo formado entre dos segmentos que unen los extremos de la cuerda AB con cualquier punto C sobre la circunferencia.
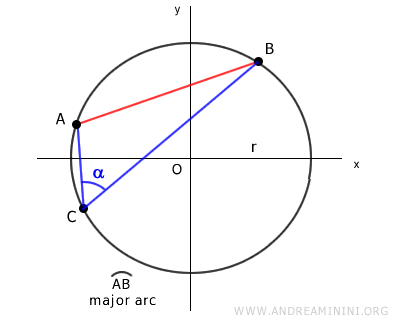
El teorema de la cuerda se cumple tanto si el punto C se encuentra sobre el arco mayor como sobre el arco menor que determina la cuerda.
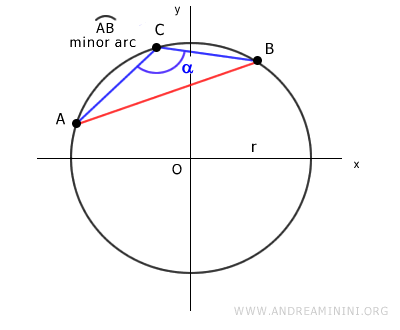
¿Para qué sirve el teorema de la cuerda? El teorema de la cuerda tiene numerosas aplicaciones. Permite calcular la longitud de cualquier cuerda en una circunferencia mediante funciones trigonométricas. Además, de este teorema se derivan otros resultados fundamentales, como la ley de senos.
Un ejemplo práctico
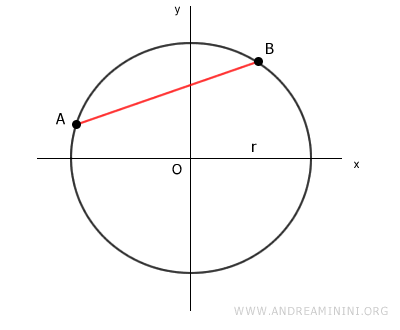
Imaginemos que dibujamos una circunferencia con radio r=3.
Por lo tanto, el diámetro de la circunferencia será seis.
$$ d = 2 \cdot r = 2 \cdot 3 = 6 $$
Seleccionamos ahora dos puntos A y B sobre la circunferencia.

Y trazamos una cuerda que une los puntos A y B.

Para calcular la longitud de dicha cuerda, aplicamos el teorema trigonométrico de la cuerda:
$$ \overline{AB} = 2r \cdot \sin \alpha $$
Sabemos que el radio es r=3.
$$ \overline{AB} = 2 \cdot 3 \cdot \sin \alpha $$
$$ \overline{AB} = 6 \cdot \sin \alpha $$
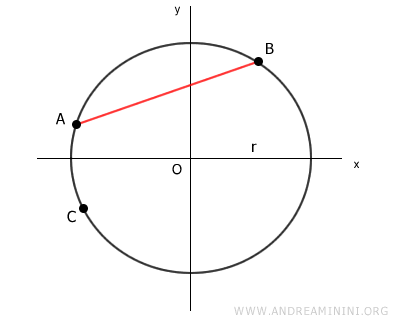
Tomamos a continuación un punto C cualquiera sobre la circunferencia.
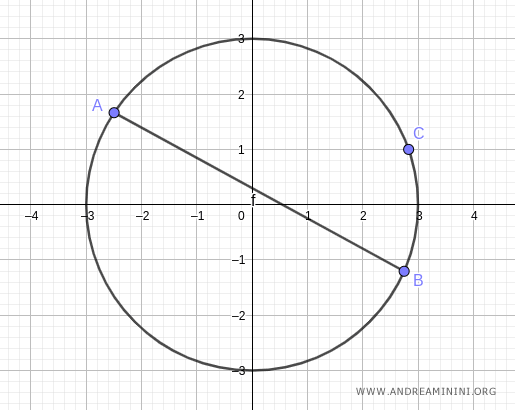
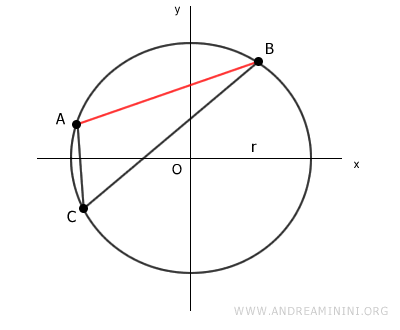
Trazamos el segmento AC, que une uno de los extremos de la cuerda con el punto C.
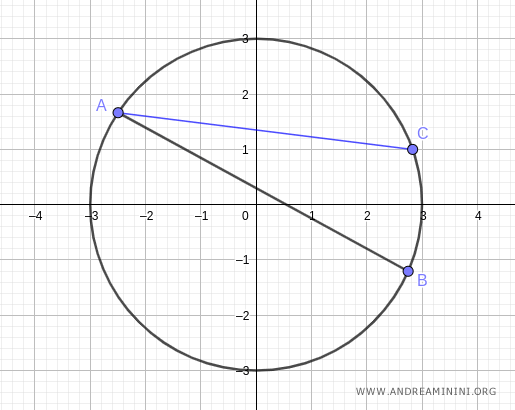
Después, trazamos el segmento BC, que conecta el otro extremo de la cuerda con el mismo punto C.
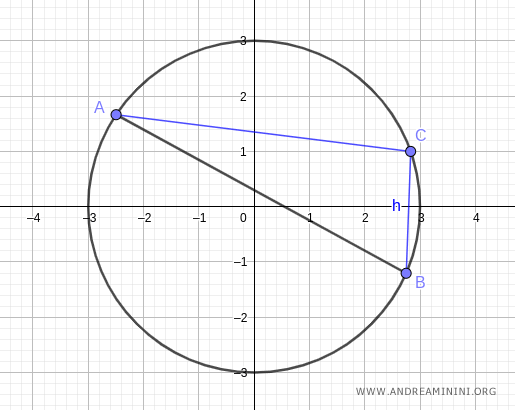
El ángulo ACB formado por los segmentos AC y BC mide α=95°.
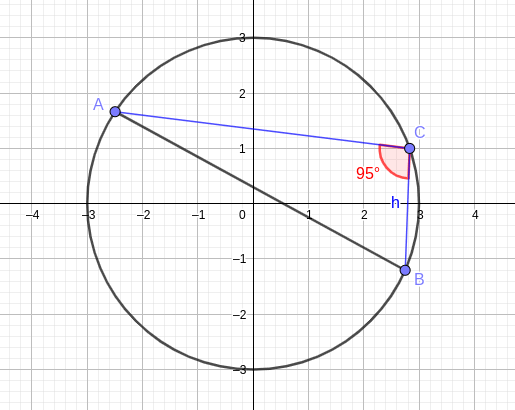
Por tanto, aplicando el teorema de la cuerda:
$$ \overline{AB} = 6 \cdot \sin \alpha $$
$$ \overline{AB} = 6 \cdot \sin 95° $$
$$ \overline{AB} = 5.98 $$
Así, la longitud de la cuerda AB resulta ser 5.98.
Nota: Escoger cualquier otro punto C sobre la circunferencia no modifica el resultado, ya que el ángulo alfa permanece constante a lo largo del arco AB.

Por ejemplo, en el arco superior AB, el ángulo mide 95°, mientras que en el arco inferior es de 85°.

En ambos casos, el ángulo mantiene su valor a lo largo de todo el arco, y el valor del seno garantiza que la longitud de la cuerda AB siga siendo 5.98.
Demostración
Consideremos una circunferencia cualquiera de radio r.
Trazamos una cuerda que une dos puntos A y B sobre la circunferencia.
Seleccionamos ahora un punto C cualquiera sobre el arco AB.
Y trazamos los segmentos AC y BC, que unen el punto C con los extremos A y B de la cuerda.
Estos dos segmentos forman el ángulo ACB, cuya medida es alfa.

A continuación, trazamos un segmento que pase por el centro O y por uno de los extremos de la cuerda AB.
Por ejemplo, el segmento AD.
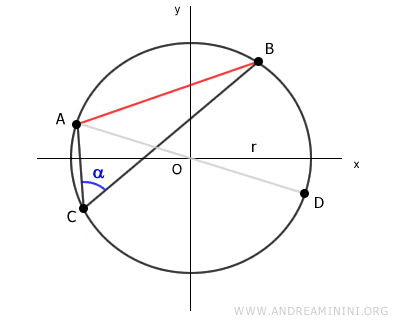
Esto define otro punto D sobre la circunferencia.
Unimos ahora el punto D con el otro extremo B de la cuerda AB.
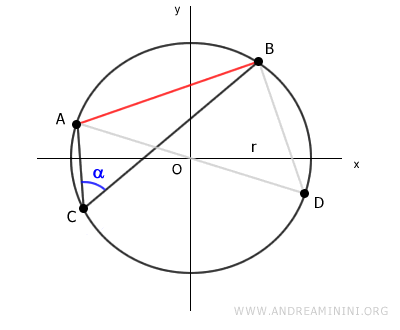
Así obtenemos el triángulo ABD.
El triángulo ABD es rectángulo, ya que está inscrito en el semicírculo definido por AD.
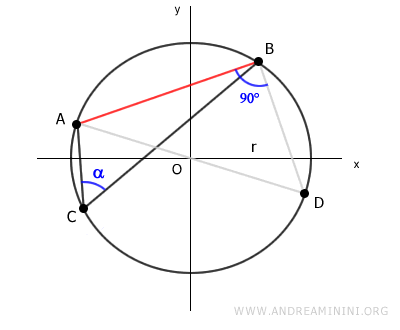
Los triángulos ABC y ABD subtienden el mismo arco AB.
Por lo tanto, el ángulo ADB es congruente con el ángulo alfa.
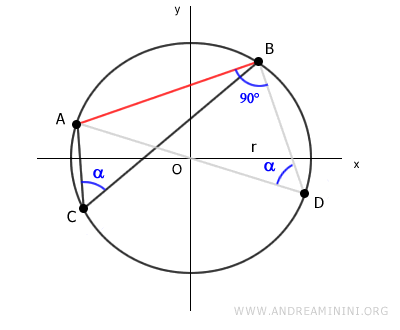
Como el triángulo ABD es rectángulo, podemos aplicar el primer teorema del triángulo rectángulo para calcular la longitud de la cuerda AB.
$$ \overline{AB} = \overline{AD} \cdot \sin \alpha $$
Nota: Según el primer teorema del triángulo rectángulo, un cateto es igual a la hipotenusa multiplicada por el seno del ángulo opuesto. En este caso, el cateto es el segmento AB, la hipotenusa es el segmento AD, y el ángulo opuesto es alfa.
El segmento AD corresponde al diámetro de la circunferencia, es decir, el doble del radio: AD = 2r.
$$ \overline{AB} = 2r \cdot \sin \alpha $$
Esto demuestra la fórmula del teorema de la cuerda para el arco mayor AB.
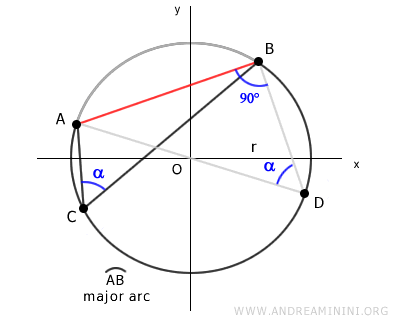
Ahora debemos demostrar que el teorema también es válido si consideramos un punto sobre el arco menor AB.
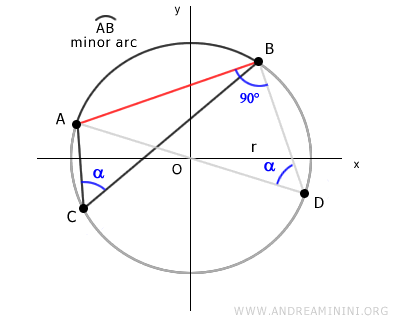
Seleccionamos cualquier punto E sobre el arco menor AB.
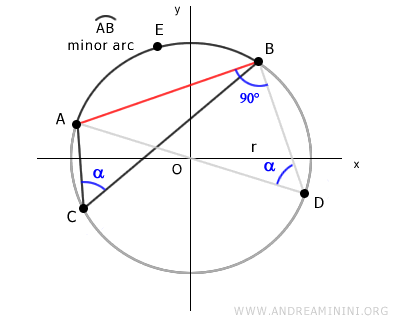
Después conectamos el punto E con los extremos A y B de la cuerda.
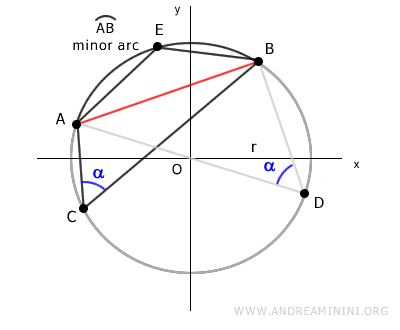
Así se forma un cuadrilátero AEBC, donde los segmentos AE y BE definen un ángulo β.
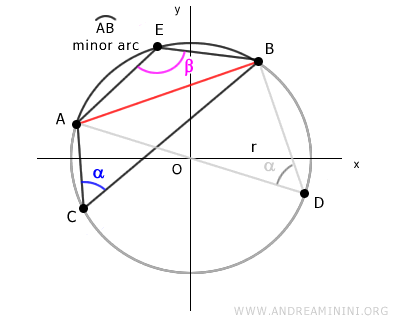
Los ángulos opuestos α y β en el cuadrilátero son suplementarios, ya que el cuadrilátero está inscrito en la circunferencia.
Por consiguiente, su suma es igual a 180° o π radianes.
$$ \alpha + \beta = \pi $$
Conocemos el ángulo alfa α.
Por lo tanto, podemos determinar el ángulo beta β.
$$ \beta = \pi - \alpha $$
Aplicamos la función seno a ambos lados de la igualdad.
$$ \sin \beta = \sin (\pi - \alpha) $$
De acuerdo con la propiedad trigonométrica de los ángulos asociados, se cumple que sen(π - α) = sen(α).
$$ \sin \beta = \sin (\pi - \alpha) = \sin \alpha $$
Esto implica que sen(β) = sen(α).
Así, el teorema de la cuerda que demostramos antes para el arco mayor AB:
$$ \overline{AB} = 2r \cdot \sin \alpha $$
también se cumple utilizando el ángulo beta en el arco menor AB:
$$ \overline{AB} = 2r \cdot \sin \alpha = 2r \cdot \sin \beta $$
Con ello, queda demostrado el teorema de la cuerda para ambos arcos AB.
Y con esto, queda concluida la demostración.