Arcocotangente
La arcocotangente es la función trigonométrica inversa de la cotangente. Se expresa de la siguiente manera: $$ y = \text{arcocotg} \ x $$ Entre sus notaciones más habituales se encuentran arcocotg, arccot, cotan-1 y cotg-1.
Desde el punto de vista geométrico, la arcocotangente mide el arco, expresado en radianes, sobre la circunferencia unitaria que corresponde al ángulo cuyo valor de cotangente es el indicado.
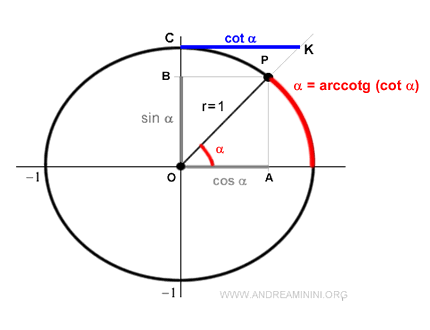
Por ejemplo, la cotangente de un ángulo de π/2 (90°) es cero:
$$ cotg \ \frac{\pi}{2} = 0 $$
Por lo tanto, la arcocotangente de cero es π/2:
$$ arcocotg \ 0 = \frac{\pi}{2} $$
Nota: Al tratarse de una función inversa, la arcocotangente de la cotangente de un ángulo devuelve dicho ángulo. $$ arcocotg \bigl( cotg \ \alpha \bigr) = \alpha $$
Gráfica de la función arcocotangente
La gráfica de la arcocotangente se encuentra acotada entre un valor máximo de π y un mínimo de 0. Es una función estrictamente decreciente.
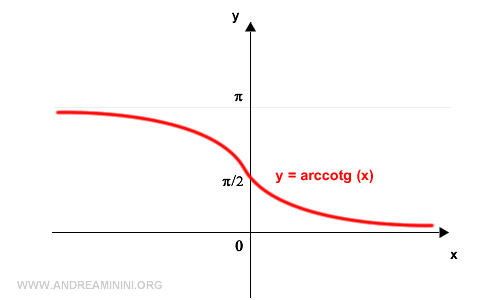
¿Cómo se construye la gráfica de la arcocotangente?
La función cotangente es periódica, lo que significa que repite sus valores a intervalos regulares.
Debido a esta periodicidad, la cotangente no es invertible en todo su dominio, ya que no es una función biyectiva (uno a uno).
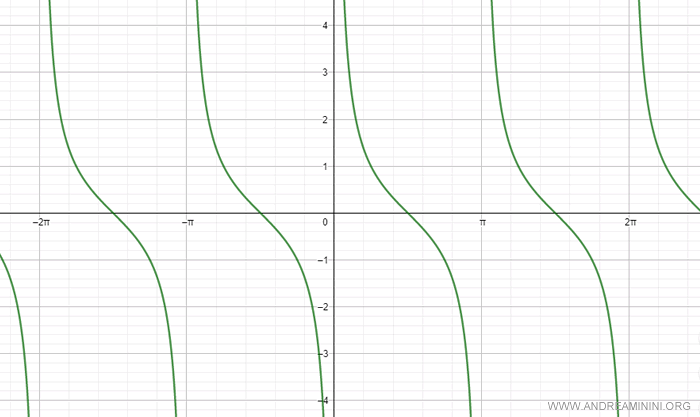
Sin embargo, si restringimos su dominio al intervalo (0, π), la cotangente se convierte en una función biyectiva (uno a uno).
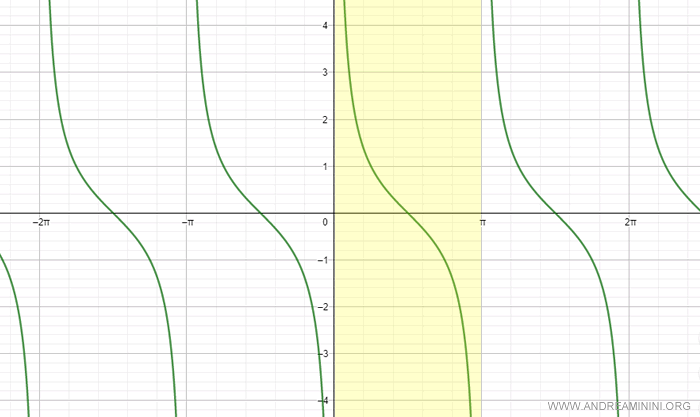
Nota: La cotangente también puede ser biyectiva en otros intervalos, como (-π, 0). Es posible elegir diferentes intervalos para definir su función inversa según el contexto.
Al ser biyectiva en el intervalo (0, π), la cotangente es invertible en dicho rango.
La función inversa de la cotangente en el intervalo (0, π) es la arcocotangente.
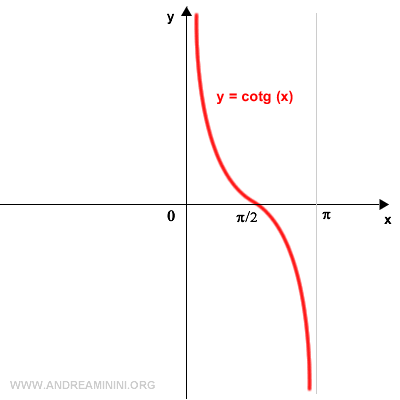
Para obtener la gráfica de la arcocotangente, se rota la gráfica de la cotangente 90° en sentido antihorario.
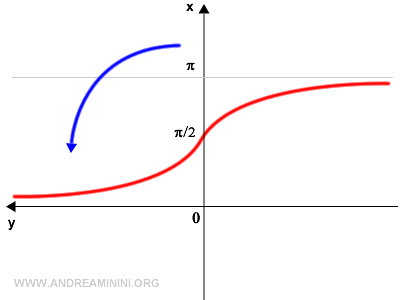
Después, se refleja la gráfica de forma horizontal respecto al eje vertical (eje x).
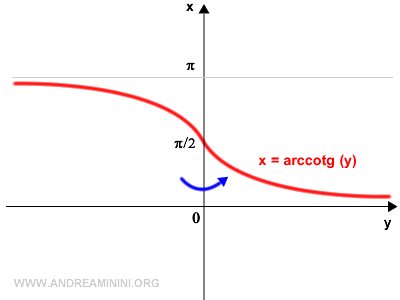
De este modo, se obtiene la gráfica de la arcocotangente.
Y eso es todo.