Ley de Senos
En todo triángulo, los lados son proporcionales a los senos de sus ángulos opuestos: $$ \frac{\overline{AB}}{\sin \gamma} = \frac{\overline{BC}}{\sin \alpha} = \frac{\overline{AC}}{\sin \beta} $$
Aquí, α, β y γ representan los ángulos opuestos a los lados BC, AC y AB, respectivamente.
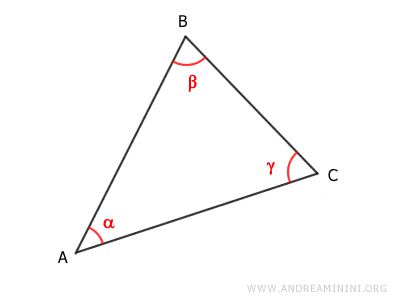
Este resultado también se conoce como la Ley de Senos de Euler.
Ejemplo Práctico
Veamos cómo resolver un triángulo
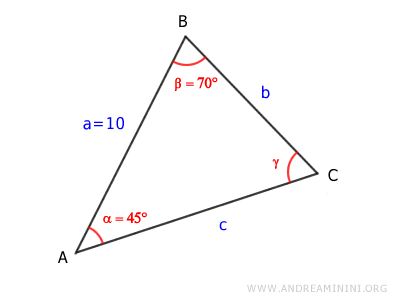
del cual conocemos dos ángulos y la longitud de uno de sus lados.
$$ \alpha = 45° $$
$$ \beta = 70° $$
$$ \overline{AB} = 10 $$
Primero, vamos a calcular el ángulo que falta.
Dado que la suma de los ángulos de un triángulo es 180°, podemos hallar γ restando α y β a 180°.
$$ \alpha + \beta + \gamma = 180° $$
$$ \gamma = 180° - \alpha - \beta $$
$$ \gamma = 180° - 45° - 70° $$
$$ \gamma = 65° $$
Ahora conocemos los tres ángulos del triángulo.
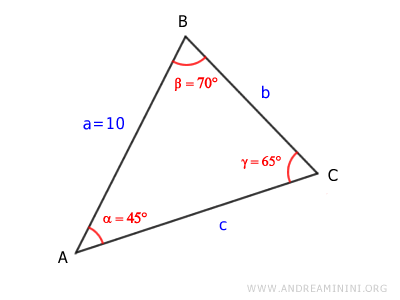
Con todos los ángulos determinados, podemos emplear la Ley de Senos para calcular las longitudes de los lados restantes.
$$ \frac{\overline{AB}}{\sin \gamma} = \frac{\overline{BC}}{\sin \alpha} = \frac{\overline{AC}}{\sin \beta} $$
$$ \frac{\overline{AB}}{\sin 65°} = \frac{\overline{BC}}{\sin 45°} = \frac{\overline{AC}}{\sin 70°} $$
Sabemos que AB mide 10, por lo que:
$$ \frac{10}{\sin 65°} = \frac{\overline{BC}}{\sin 45°} = \frac{\overline{AC}}{\sin 70°} $$
Igualamos la primera y la segunda razón para calcular la longitud de BC:
$$ \frac{10}{\sin 65°} = \frac{\overline{BC}}{\sin 45°} $$
$$ \overline{BC} = \frac{10}{\sin 65°} \cdot \sin 45° $$
$$ \overline{BC} = 7.8 $$
Luego, igualamos la primera y la tercera razón para obtener la longitud de AC:
$$ \frac{10}{\sin 65°} = \frac{\overline{AC}}{\sin 70°} $$
$$ \overline{AC} = \frac{10}{\sin 65°} \cdot \sin 70° $$
$$ \overline{AC} = 10.37 $$
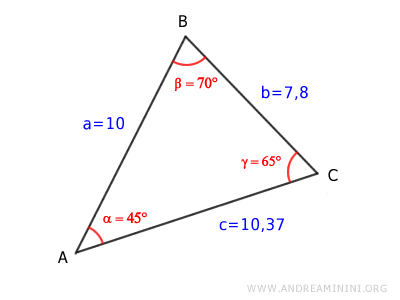
Por tanto, las longitudes de los lados del triángulo son:
$$ \overline{AB} = 10 $$
$$ \overline{BC} = 7.8 $$
$$ \overline{AC} = 10.37 $$
Hemos resuelto por completo el triángulo.
La Demostración
Consideremos cualquier triángulo inscrito en una circunferencia de radio r.
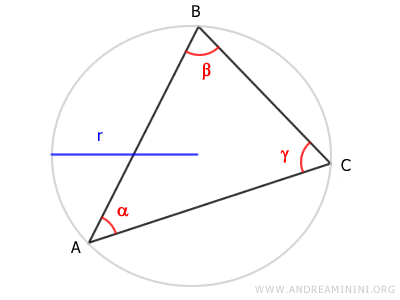
De acuerdo con el Teorema de la Cuerda, cada lado del triángulo es igual al producto del diámetro de la circunferencia (2r) por el seno del ángulo opuesto.
$$ \overline{AB} = 2r \cdot \sin \gamma $$
$$ \overline{AC} = 2r \cdot \sin \beta $$
$$ \overline{BC} = 2r \cdot \sin \alpha $$
Destacando el diámetro (2r) en cada expresión, obtenemos:
$$ \frac{ \overline{AB} }{ \sin \gamma } = 2r $$
$$ \frac{ \overline{AC} }{ \sin \beta } = 2r $$
$$ \frac{ \overline{BC} }{ \sin \alpha } = 2r $$
Por lo tanto, cada razón es igual al diámetro 2r.
Esto nos lleva a la siguiente igualdad:
$$ \frac{ \overline{AB} }{ \sin \gamma } = \frac{ \overline{AC} }{ \sin \beta } = \frac{ \overline{BC} }{ \sin \alpha } = 2r $$
Con ello, se demuestra que los lados del triángulo son proporcionales a los senos de sus ángulos opuestos:
$$ \frac{ \overline{AB} }{ \sin \gamma } = \frac{ \overline{AC} }{ \sin \beta } = \frac{ \overline{BC} }{ \sin \alpha } $$
Y, de este modo, queda demostrada la Ley de Senos.
Y así sucesivamente.