Cálculo del Área de un Triángulo Usando Trigonometría
El área de un triángulo se obtiene multiplicando la mitad del producto de dos lados l1 y l2 por el seno del ángulo (α) comprendido entre ellos. $$ Área = \frac{1}{2} \cdot (l_1 \cdot l_2) \cdot \sin \alpha $$
En esta fórmula, l1 y l2 son dos lados consecutivos del triángulo, y α es el ángulo formado entre ellos.
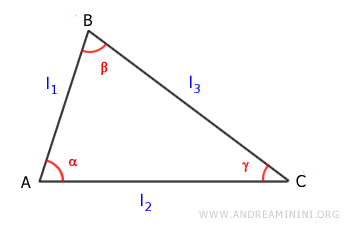
De manera análoga, también se cumplen las siguientes fórmulas:
$$ Área = \frac{1}{2} \cdot (l_1 \cdot l_3) \cdot \sin \beta $$
$$ Área = \frac{1}{2} \cdot (l_2 \cdot l_3) \cdot \sin \gamma $$
Estas expresiones son aplicables a cualquier tipo de triángulo, ya sea isósceles, rectángulo o escaleno.
Ejemplo Práctico
Veamos primero un triángulo rectángulo.
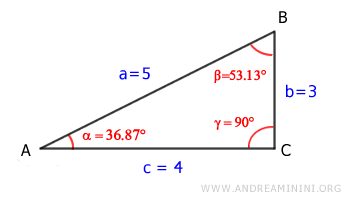
Su área se calcula como base (c) por altura (b), dividido entre dos.
$$ Área = \frac{1}{2} (c \cdot b) = \frac{1}{2} (4 \cdot 3) = 6 $$
Ahora vamos a calcular el área usando trigonometría.
Consideremos los lados adyacentes a = 5, c = 4 y el ángulo comprendido α = 36.87°.
$$ Área = \frac{1}{2} (a \cdot c) \sin \alpha $$
$$ Área = \frac{1}{2} (5 \cdot 4) \sin 36.87° $$
$$ Área = \frac{1}{2} (20) \cdot 0.6 $$
$$ Área = 6 $$
El resultado coincide perfectamente.
Si ahora tomamos los lados a = 5, b = 3 y el ángulo comprendido β = 53.13°, obtendremos el mismo valor.
$$ Área = \frac{1}{2} (a \cdot b) \sin \beta $$
$$ Área = \frac{1}{2} (5 \cdot 3) \sin 53.13° $$
$$ Área = \frac{1}{2} (15) \cdot 0.8 $$
$$ Área = 6 $$
De manera similar, si consideramos los lados c = 4, b = 3 y el ángulo comprendido γ = 90°, el área también es la misma.
$$ Área = \frac{1}{2} (c \cdot b) \sin \gamma $$
$$ Área = \frac{1}{2} (4 \cdot 3) \sin 90° $$
$$ Área = \frac{1}{2} (12) \cdot 1 $$
$$ Área = 6 $$
En todos los casos, el área del triángulo resulta ser 6.
Ejemplo 2
En este ejemplo analizamos un triángulo isósceles.
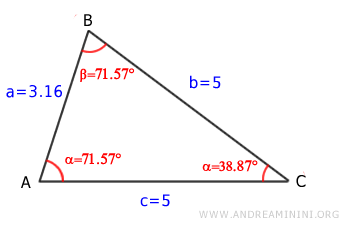
Calculamos el área utilizando los lados b = 5 y c = 5, y el ángulo comprendido γ = 36.87°.
$$ Área = \frac{1}{2} (b \cdot c) \sin \gamma $$
$$ Área = \frac{1}{2} (5 \cdot 5) \sin 36.87° $$
$$ Área = \frac{1}{2} (25) \cdot 0.6 $$
$$ Área = 7.5 $$
Alternativamente, podemos calcular el área usando los lados a = 3.16 y c = 5, y el ángulo comprendido α = 71.57°.
$$ Área = \frac{1}{2} (a \cdot c) \sin \alpha $$
$$ Área = \frac{1}{2} (3.16 \cdot 5) \sin 71.57° $$
$$ Área = 7.5 $$
O bien, empleando los lados a = 3.16 y b = 5, y el ángulo β = 71.57°.
$$ Área = \frac{1}{2} (3.16 \cdot 5) \sin 71.57° $$
$$ Área = 7.5 $$
En todos los casos, el área obtenida es la misma.
Así, el área del triángulo es 7.5.
Demostración
Caso 1
Analicemos primero un triángulo rectángulo.
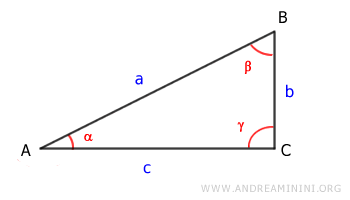
Sabemos que el área de un triángulo se calcula como base (c) por altura (b), dividido entre dos.
$$ Área = \frac{1}{2} \cdot c \cdot b $$
Según el primer teorema de los triángulos rectángulos, la longitud del cateto b (altura) equivale a la hipotenusa (a) por el seno del ángulo opuesto (α), es decir, b = a \sin \alpha.
$$ Área = \frac{1}{2} \cdot c \cdot (a \cdot \sin \alpha) $$
$$ Área = \frac{1}{2} \cdot (c \cdot a) \cdot \sin \alpha $$
Aquí, α es el ángulo comprendido entre los lados a y c del triángulo.
Así, obtenemos la fórmula que queríamos demostrar.
Caso 2
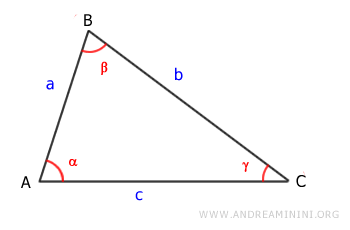
Consideremos un triángulo isósceles con lados b = c y ángulos congruentes α = β.
Se traza la altura (h) del triángulo, representada por el segmento BD.
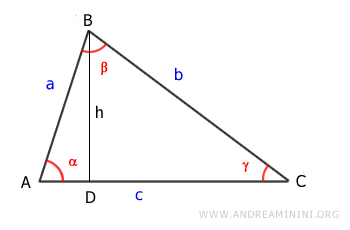
El área del triángulo es base (c) por altura (h), dividido entre dos.
$$ Área = \frac{1}{2} \cdot c \cdot h $$
La altura (h) corresponde al cateto del triángulo rectángulo ABD.
Por el primer teorema de los triángulos rectángulos, la longitud del segmento BD (la altura h) es igual a la hipotenusa (AB) por el seno del ángulo opuesto (α), es decir, h = a \sin \alpha.
$$ Área = \frac{1}{2} \cdot c \cdot a \cdot \sin \alpha $$
Aquí, el ángulo agudo α es el ángulo comprendido entre los lados a y c del triángulo isósceles.
De este modo, llegamos nuevamente a la fórmula que queríamos demostrar.
Caso 3
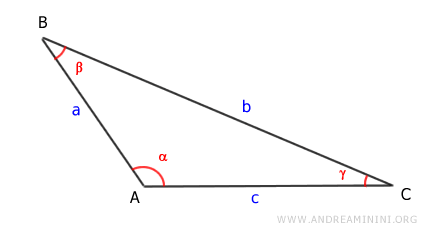
Consideremos ahora un triángulo escaleno con un ángulo obtuso (α).
Se traza la altura (h) del triángulo, correspondiente al segmento AD.
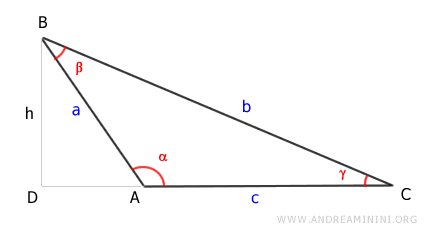
El área se obtiene multiplicando base (c) por altura (h), dividido entre dos.
$$ Área = \frac{1}{2} \cdot c \cdot h $$
La altura h corresponde al cateto AD del triángulo rectángulo ADB.
Por el primer teorema de los triángulos rectángulos, la longitud de AD (la altura h) es igual a la hipotenusa (AB) multiplicada por el seno del ángulo opuesto (π-α), es decir, h = a \sin (\pi - \alpha).
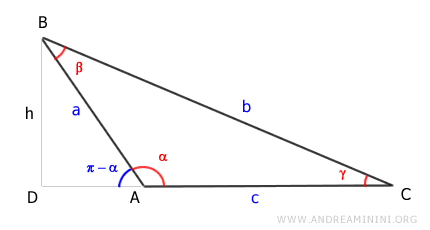
Sustituyendo h por a \sin(\pi - \alpha), obtenemos:
$$ Área = \frac{1}{2} \cdot c \cdot h $$
$$ Área = \frac{1}{2} \cdot c \cdot a \cdot \sin (\pi - \alpha) $$
El ángulo (π-α) es el ángulo suplementario del ángulo obtuso α.
Sabiendo que, por la propiedad de los ángulos asociados, se cumple que \sin(\pi - \alpha) = \sin(\alpha), podemos reescribir la fórmula así:
$$ Área = \frac{1}{2} \cdot c \cdot a \cdot \sin (\alpha) $$
En este caso, el ángulo obtuso α es el ángulo comprendido entre los lados a y c del triángulo escaleno.
De este modo, volvemos a obtener la fórmula que queríamos demostrar.
En conclusión, la fórmula para calcular el área es válida para cualquier tipo de triángulo.
Y así sucesivamente.