Un método fácil para memorizar seno, coseno y tangente en los ángulos 0°, 30°, 45°, 60°, 90°
Este método utiliza los dedos de una mano para recordar de manera sencilla los valores de seno, coseno y tangente en los ángulos 0°, 30°, 45°, 60° y 90°.
El truco consiste en contar los dedos que quedan a la izquierda y a la derecha del dedo que representa un ángulo dado.
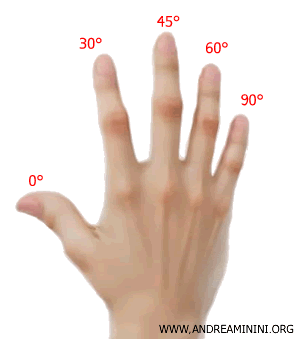
Cada dedo de la mano derecha corresponde a un ángulo $ \alpha $:
- Pulgar: 0°
- Índice: 30°
- Medio: 45°
- Anular: 60°
- Meñique: 90°
Para calcular el coseno, el seno y la tangente de un ángulo $ \alpha $, basta con identificar el dedo correspondiente y aplicar las siguientes reglas:
- Coseno del ángulo
El coseno de $ \alpha $ es la raíz cuadrada del número de dedos situados a la derecha del dedo en cuestión, dividido entre 2: $$ \cos( \alpha ) = \frac{ \sqrt{ \text{n.º de dedos a la derecha} } }{2} $$ - Seno del ángulo
El seno de $ \alpha $ es la raíz cuadrada del número de dedos situados a la izquierda del dedo en cuestión, dividido entre 2: $$ \sin( \alpha ) = \frac{ \sqrt{ \text{n.º de dedos a la izquierda} } }{2} $$ - Tangente del ángulo
La tangente de $ \alpha $ se obtiene dividiendo el seno entre el coseno: $$ \tan{\alpha} = \frac{ \sin{ \alpha } }{ \cos{ \alpha }} $$
De este modo, con una sola mano puedes obtener rápidamente los valores trigonométricos de estos ángulos.
Nota: Si prefieres usar la mano izquierda, basta con invertir las fórmulas del seno y el coseno. En mi caso utilizo la derecha porque resulta más fácil de recordar.
Ejemplo práctico
Calculemos el coseno, seno y tangente de 60°.
El ángulo de 60° corresponde al dedo anular de la mano derecha.
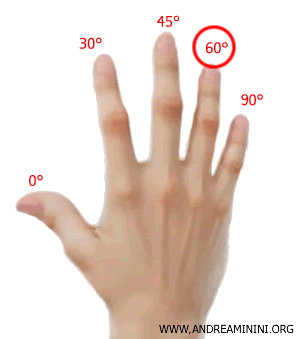
A la derecha del anular solo hay un dedo (el meñique), por lo que el coseno de 60° es:
$$ \cos( 60° ) = \frac{ \sqrt{ \text{n.º de dedos a la derecha} } }{2} = \frac{ \sqrt{1} }{2} = \frac{1}{2} $$
A la izquierda del anular hay tres dedos, así que el seno de 60° es:
$$ \sin( 60° ) = \frac{ \sqrt{ \text{n.º de dedos a la izquierda} } }{2} = \frac{ \sqrt{3} }{2} $$
Por último, con los valores de seno y coseno ya obtenidos, calculamos la tangente de 60° aplicando la relación $ \tan(a)=\sin(a)/\cos(a) $:
$$ \tan(60°) = \frac{\sin(60°)}{\cos(60°)} = \frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} = \sqrt{3} $$
Los resultados coinciden con los valores exactos de la tabla trigonométrica.
| Ángulo | Seno | Coseno | Tangente | |
|---|---|---|---|---|
| Radianes | Grados | |||
| 0 | 0° | 0 | 1 | 0 |
| π/6 | 30° | 1/2 | √3/2 | √3/3 |
| π/4 | 45° | √2/2 | √2/2 | 1 |
| π/3 | 60° | √3/2 | 1/2 | √3 |
| π/2 | 90° | 1 | 0 | ∞ |
Y así sucesivamente.