Arcotangente
¿Qué es la arcotangente?
En trigonometría, la arcotangente es la función inversa de la tangente. Se suele denotar como arctg, arctan, tg-1 o tan-1. $$ y = \arctan \ x $$
En esta expresión, x representa el valor de la tangente.
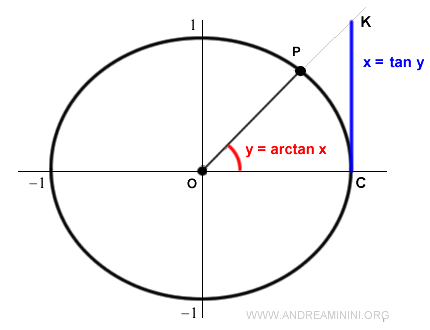
La función arcotangente devuelve el ángulo y cuyo valor de tangente es x.
$$ y = \arctan \ x $$
donde x es el valor de la tangente.
$$ x = \tan y $$
El gráfico de la función arcotangente es el siguiente:
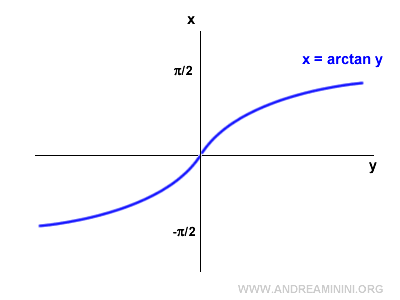
Nota: El dominio de la arcotangente es todo el conjunto de los números reales, ya que coincide con el recorrido de la función tangente. $$ D_{arctan} = ( -\infty ; +\infty ) $$ Su imagen, sin embargo, está acotada en el intervalo [-π/2, π/2].
Un ejemplo práctico
La tangente de π/4 es igual a 1:
$$ \tan \frac{\pi}{4} = 1 $$
Como la arcotangente es la función inversa de la tangente,
la arcotangente de 1 es π/4:
$$ \arctan 1 = \frac{\pi}{4} $$
Nota: Aplicar la arcotangente a la tangente de un ángulo devuelve el ángulo original. $$ \arctan (\tan \frac{\pi}{4}) = \frac{\pi}{4} $$
Cómo se construye el gráfico de la arcotangente
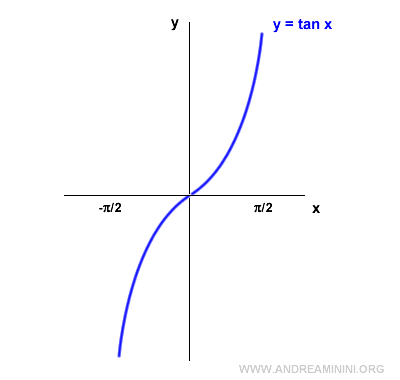
Partimos del gráfico de la función tangente:
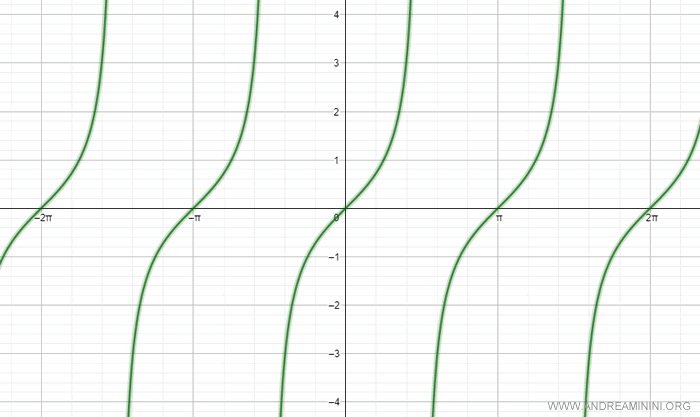
La función tangente no es invertible en todo su dominio, ya que no es una función inyectiva (biunívoca).
Para hacerla invertible, se restringe su dominio al intervalo [-π/2, π/2].
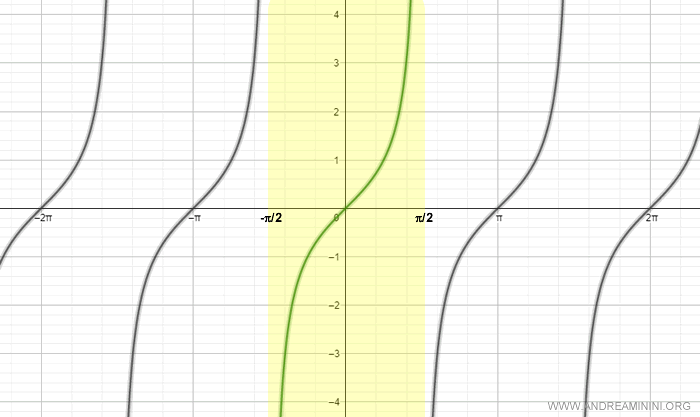
En este intervalo, la función tangente es biunívoca y, por tanto, tiene inversa.
A continuación, se rota el gráfico 90° en sentido antihorario.
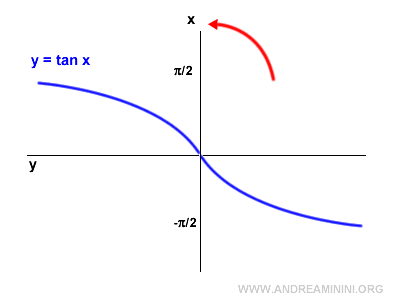
Luego se refleja horizontalmente con respecto al eje vertical.
El resultado es el gráfico de la arcotangente.
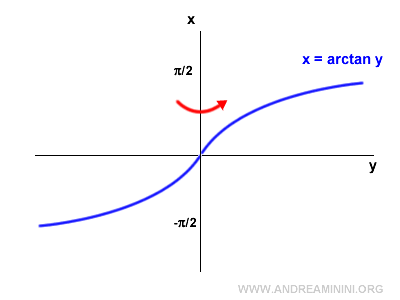
La arcotangente también es una función invertible.
Su inversa es la función tangente, restringida al intervalo [-π/2, π/2].
Nota: La tangente también puede hacerse invertible en otros intervalos donde sea biunívoca, como por ejemplo en [π/2, 3π/2]. En ese caso, el valor de la arcotangente pertenecerá al intervalo considerado.
Y así sucesivamente.