Segunda Ley Fundamental de la Trigonometría

La tangente de un ángulo se define como el cociente entre el seno y el coseno de dicho ángulo: $$ \tan \alpha = \frac{ \sin \alpha }{ \cos \alpha } $$

Demostración

Consideremos el ángulo α en la circunferencia unitaria.

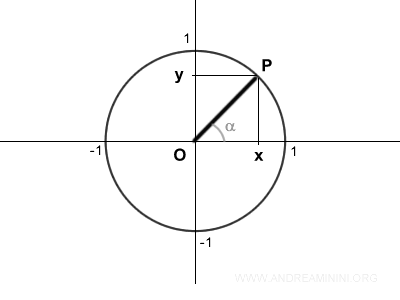
El segmento OP se sitúa sobre la recta r.

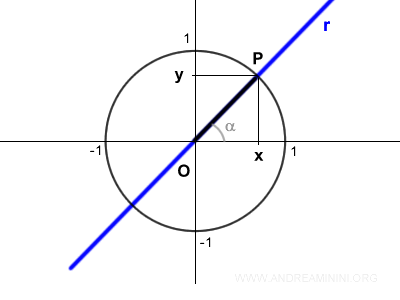
La ecuación de una recta que pasa por el origen tiene la forma y = m·x, donde m representa la pendiente, la cual determina la inclinación de la recta:

$$ y = m \cdot x $$

Multiplicamos ambos miembros por 1/x para aislar m:

$$ y \cdot \frac{1}{x} = m \cdot x \cdot \frac{1}{x} $$

Al simplificar, se obtiene:

$$ \frac{y}{x} = m $$

Así, la pendiente m de la recta r es igual a la razón entre y y x:

$$ m = \frac{y}{x} $$

Se sabe que la pendiente de la recta coincide con la tangente del ángulo α (véase esta explicación):

$$ m = \frac{y}{x} = \tan \alpha $$

En la circunferencia unitaria, el valor de y corresponde a sin α, y el de x a cos α:

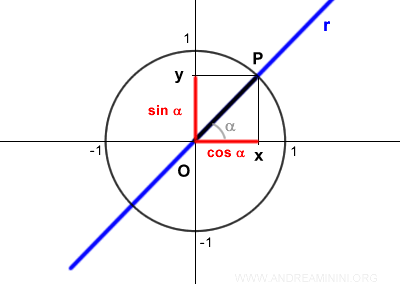
Por tanto, podemos escribir:

$$ m = \frac{y}{x} = \frac{\sin \alpha}{ \cos \alpha } = \tan \alpha $$

De este modo, queda demostrada la segunda ley fundamental de la trigonometría:

$$ \frac{\sin \alpha}{ \cos \alpha } = \tan \alpha $$

Y con ello, concluimos la demostración.