Función Arcoseno
¿Qué es el arcoseno?
El arcoseno es la función trigonométrica inversa del seno, definida en el intervalo [-π/2, +π/2]. Se denota comúnmente como arcsen o arcsin.
En ocasiones también se representa como sin-1, donde el exponente -1 indica que se trata de la función inversa, y no de una potencia. Para evitar ambigüedades, suele preferirse la notación arcsin.
¿Cómo funciona el arcoseno?
Dado un valor de seno \( y \), la función arcoseno permite determinar el ángulo \( x \), expresado en radianes, cuyo seno es precisamente ese valor.
Ejemplo
Supongamos que el seno de un ángulo es 0,75:
$$ \sin \: x = 0{,}75 $$
¿Qué valor de \( x \) corresponde a este resultado?
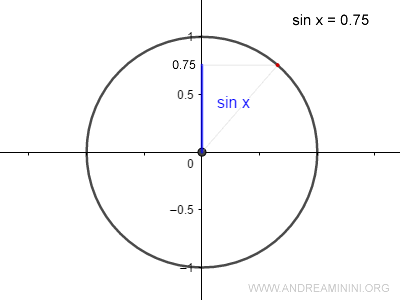
Para encontrar dicho ángulo, basta con calcular el arcoseno de 0,75:
$$ x = \arcsin(0{,}75) \approx 0{,}848 $$
El arcoseno nos da la medida del arco en la circunferencia unitaria que corresponde a ese valor de seno.
Dicho arco se mide en radianes y tiene la misma amplitud que el ángulo \( x \) que genera ese seno.
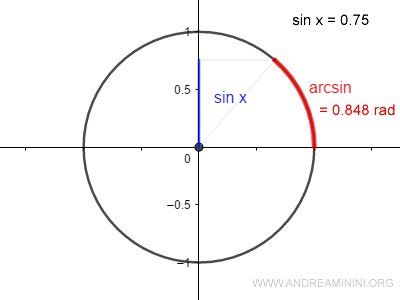
En este caso, el ángulo que tiene un seno igual a 0,75 es aproximadamente 0,848 radianes.
Explicación
La función seno toma valores comprendidos entre -1 y +1.
Como se trata de una función periódica, un mismo valor de seno puede corresponder a múltiples ángulos distintos.
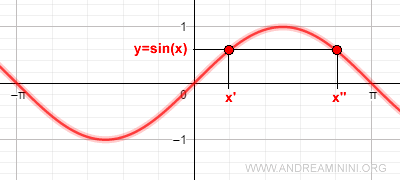
Esta característica hace que no sea posible definir una función inversa para el seno sobre todo su dominio, ya que se violaría la condición de unicidad: una función no puede asignar dos valores distintos de \( x \) al mismo valor de \( y \).
$$ f: x \rightarrow y $$
¿Cómo se construye entonces la inversa del seno?
La solución consiste en restringir el dominio de la función seno a un intervalo donde sea estrictamente creciente (o decreciente), y por tanto inyectiva.
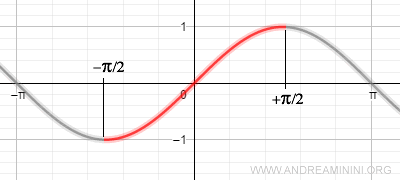
Al limitar su dominio al intervalo [-π/2, +π/2], se garantiza una correspondencia biunívoca entre los valores del seno (entre -1 y +1) y los ángulos \( x \).
En ese intervalo, la función seno es biyectiva, lo que permite definir su inversa.
De este modo, se puede construir la función inversa del seno.
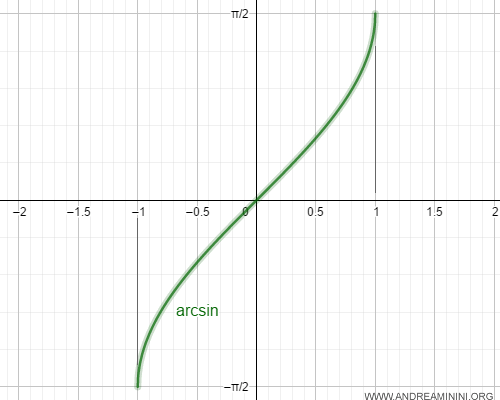
Esta función inversa recibe el nombre de arcoseno.
$$ \arcsin(x): [-1,1] \rightarrow [-\pi/2, \pi/2] $$
La notación estándar es arcsin.
A partir de un valor de seno, la función arcoseno devuelve el ángulo \( x \) correspondiente en el intervalo [-π/2, π/2].
Nota: El intervalo [-π/2, π/2] no es el único en el que la función seno puede hacerse invertible. También puede definirse una inversa en intervalos como [π/2, 3π/2], o en cualquier otro donde el seno sea biyectivo.
¿Cómo se construye la gráfica del arcoseno?
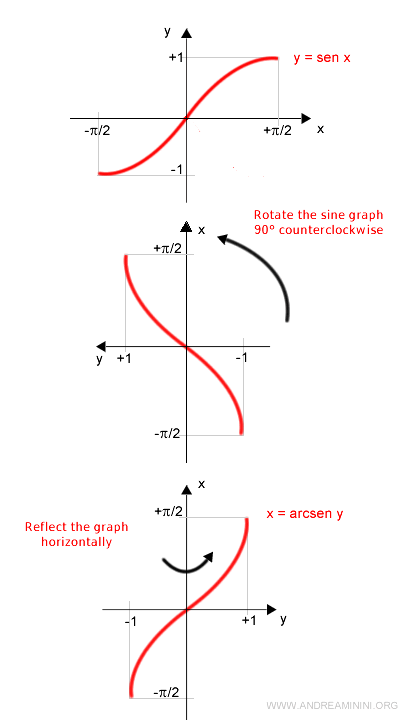
La gráfica de la función arcoseno se puede obtener a partir de la del seno (restringida al intervalo [-π/2, π/2]) mediante los siguientes pasos:
- Rotar la gráfica del seno 90° en sentido antihorario.
- Reflejarla con respecto al eje horizontal.
El resultado es la gráfica de la función arcoseno.
Del mismo modo, es posible construir otras gráficas del arcoseno utilizando diferentes intervalos de restricción donde el seno sea invertible.
Por ejemplo, a partir del intervalo [π/2, 3π/2] u otros similares.
Y así sucesivamente.