Radianes
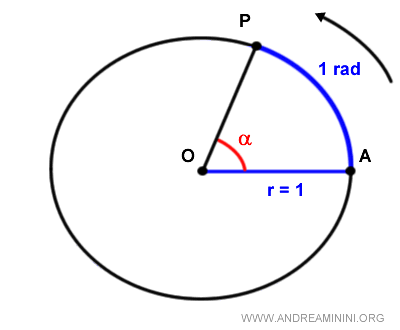
En una circunferencia unitaria, un radián es el ángulo que abarca un arco cuya longitud es exactamente igual al radio.
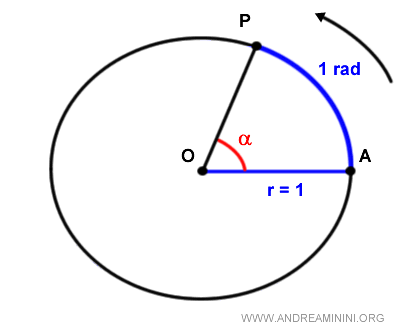
Un radián equivale aproximadamente a 57,3° en el sistema sexagesimal.
Los radianes constituyen la unidad de medida estándar para expresar ángulos.
Se simbolizan con las letras “rad”.
Nota: Existen otras unidades para medir ángulos. No obstante, salvo indicación expresa, se sobreentiende que la medida está en radianes, incluso si no se especifica el símbolo rad.
Demostración
Consideremos el mismo ángulo α inscrito en dos circunferencias de radios distintos, r y r'.
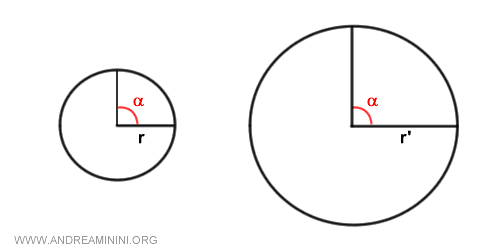
Si midiéramos el ángulo en función de la longitud del arco, obtendríamos dos valores diferentes.
Para el mismo ángulo, la segunda circunferencia tiene un arco más largo (k'>k) que la primera.
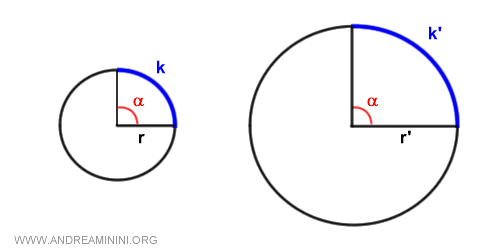
De acuerdo con la proporcionalidad entre ángulos y arcos:
$$ k : \alpha = 2 \pi r : 360° $$
$$ k' : \alpha = 2 \pi r' : 360° $$
Esto implica:
$$ \frac{k}{\alpha} = \frac{2 \pi r}{360°} $$
$$ \frac{k'}{\alpha} = \frac{2 \pi r'}{360°} $$
Despejando las longitudes de los arcos:
$$ k = \frac{2 \pi r \cdot \alpha}{360°} $$
$$ k' = \frac{2 \pi r' \cdot \alpha}{360°} $$
Simplificando 2 y 360:
$$ k = \frac{\pi r \alpha}{180°} $$
$$ k' = \frac{\pi r' \alpha}{180°} $$
Dividiendo ambos términos:
$$ \frac{k}{k'} = \frac{\frac{\pi r \alpha}{180°}}{\frac{\pi r' \alpha}{180°}} $$
$$ \frac{k}{k'} = \frac{\pi r \alpha}{180°} \cdot \frac{180°}{\pi r' \alpha} $$
$$ \frac{k}{k'} = \frac{r}{r'} $$
Colocando las magnitudes correspondientes a la primera circunferencia en un lado y las de la segunda en el otro:
$$ \frac{k}{r} = \frac{k'}{r'} $$
Observamos que la relación entre la longitud del arco y el radio es idéntica en ambas circunferencias:
$$ k : r = k' : r' $$
Esto significa que el cociente entre el arco y el radio (k/r) no varía con el tamaño de la circunferencia.
Por tanto, el cociente k/r constituye una unidad universal y fiable para expresar la medida de un ángulo, pues permite comparar ángulos de circunferencias de diferentes radios.
$$ \alpha = \frac{k}{r} $$
Este cociente k/r recibe el nombre de radián (rad) y es igual a 1 cuando la longitud del arco k coincide exactamente con la longitud del radio r.
Medidas de ángulos clave en radianes y grados
La siguiente tabla recoge las medidas más frecuentes de ángulos expresadas en grados y radianes:
| Grados | Radianes |
|---|---|
| 0° | 0 |
| 15° | π/12 |
| 30° | π/6 |
| 45° | π/4 |
| 60° | π/3 |
| 90° | π/2 |
| 120° | 2/3 π |
| 135° | 3/4 π |
| 150° | 5/6 π |
| 180° | π |
| 270° | 3/2 π |
| 360° | 2 π |
¿Cómo recordarlos todos? Al principio puede parecer complicado. Sin embargo, si recuerdas que $$ 15° = \frac{\pi}{12} \ rad $$ puedes deducir fácilmente el resto: $$ 30° = 2 \cdot 15° = 2 \cdot \frac{\pi}{12} = \frac{\pi}{6} \ rad $$ $$ 45° = 3 \cdot 15° = 3 \cdot \frac{\pi}{12} = \frac{\pi}{4} \ rad $$ $$ 60° = 4 \cdot 15° = 4 \cdot \frac{\pi}{12} = \frac{\pi}{3} \ rad $$ $$ 90° = 6 \cdot 15° = 6 \cdot \frac{\pi}{12} = \frac{\pi}{2} \ rad $$ Otra forma práctica, para cálculos más exactos, es recordar que 1° equivale a: $$ 1° = \frac{2\pi}{360} = \frac{\pi}{180} \ rad $$ Y así sucesivamente.
¿Por qué una circunferencia completa mide 2π radianes?
Consideremos la circunferencia completa, correspondiente a un ángulo de 360°.
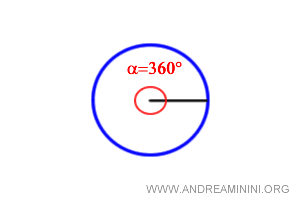
Sabemos que la longitud de una circunferencia se calcula multiplicando el radio r por 2 pi (π).
$$ k = 2 \pi r $$
Conocida la longitud de la circunferencia (k) y el radio (r), podemos hallar el ángulo en radianes mediante la fórmula:
$$ \alpha = \frac{k}{r} \ rad $$
Sustituyendo k por 2πr, obtenemos:
$$ \alpha = \frac{2 \pi r}{r} \ rad $$
Al simplificar, encontramos el valor de la circunferencia en radianes:
$$ \alpha = 2 \pi \ rad $$
Considerando que pi (π) es aproximadamente 3,14:
$$ \alpha = 2 \cdot 3,14 \ rad = 6,28 \ rad $$
En conclusión, una circunferencia completa (360°) mide 2π radianes, es decir, 6,28 radianes.
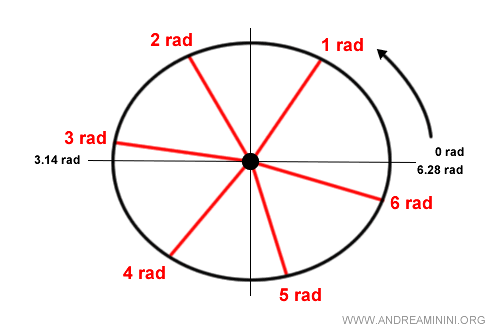
Nota: Si una circunferencia completa (360°) equivale a 2π radianes, entonces un ángulo llano (180°) equivale a π radianes, es decir, 3,14 radianes, ya que representa exactamente la mitad. Por tanto, un ángulo recto (90°) equivale a π/2 radianes. Y así sucesivamente.
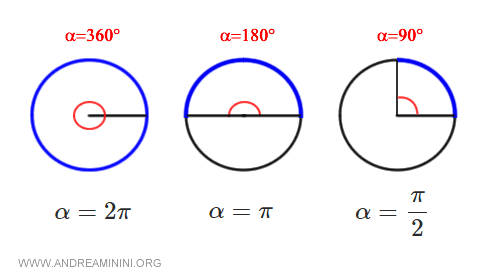
Y así sucesivamente.