Secante
¿Qué es la secante?
En trigonometría, la secante es una función que asigna a un ángulo α el recíproco del coseno. Se representa con la abreviatura sec y se define mediante la siguiente fórmula: $$ \sec \alpha = \frac{1}{\cos \alpha} $$
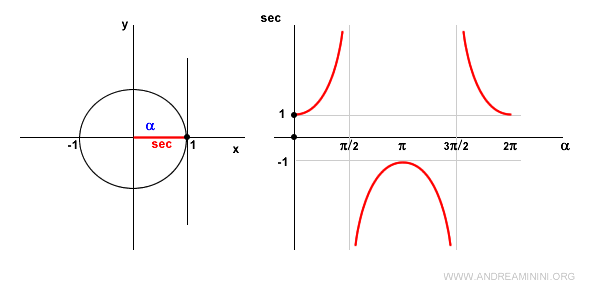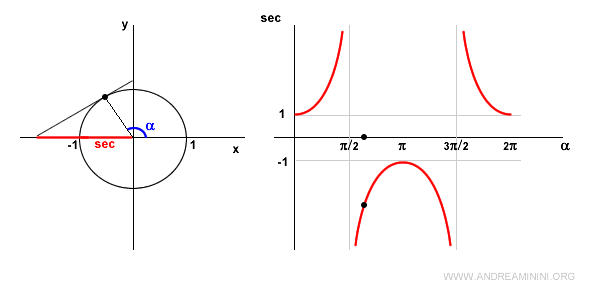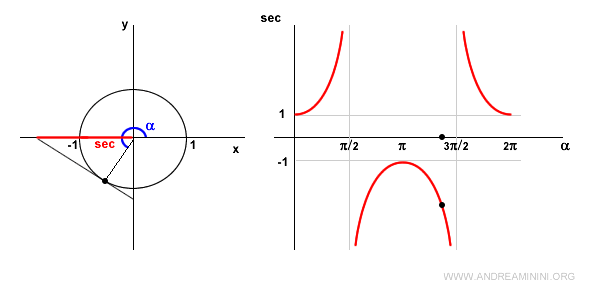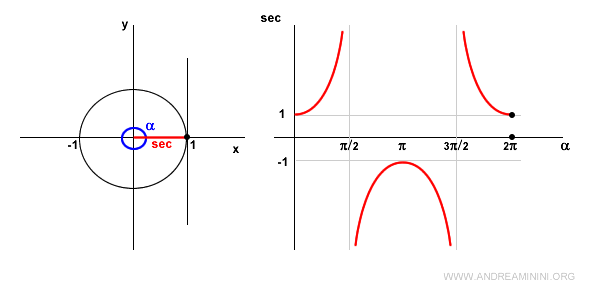
Desde un punto de vista geométrico, la secante (OB) corresponde al punto donde la recta (r), tangente al círculo unitario en el punto P, corta al eje x.
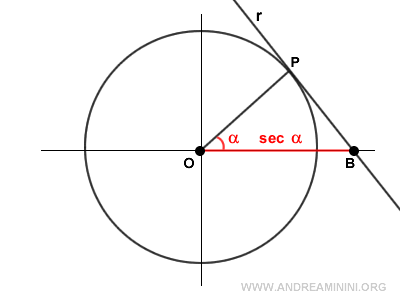
También puede interpretarse como el segmento OC, que parte del origen O, pasa por el punto P e intercepta la tangente en el punto C.
La función secante está definida para todos los números reales, excepto en los valores \( \frac{\pi}{2} + k\pi \), donde el coseno se anula y, por tanto, la función no tiene sentido.
$$ \sec \alpha \ : \ \mathbb{R} \setminus \left( \frac{\pi}{2} + k \cdot \pi \right) \longrightarrow \mathbb{R} \setminus (-1,1) \quad \text{con } k \in \mathbb{Z} $$
El codominio está compuesto por todos los números reales, excepto el intervalo abierto (-1, 1).
Desde el punto de vista analítico, la secante es una función par, ya que verifica \( f(x) = f(-x) \).
Además, es una función periódica, y su estudio puede limitarse sin pérdida de generalidad al intervalo \( (0, 2\pi) \).
Nota: La función secante no está definida en los puntos \( \frac{\pi}{2} + k\pi \), con \( k \in \mathbb{Z} \), donde presenta una asíntota vertical.
A continuación se muestran algunos valores característicos de la función secante que conviene memorizar:
| Grados | Radianes | Secante |
|---|---|---|
| 0° | 0 | 1 |
| 45° | π/4 | √2 |
| 60° | π/3 | 2 |
| 90° | π/2 | indefinida |
| 120° | 2π/3 | -2 |
| 180° | π | -1 |
| 270° | 3π/2 | indefinida |
| 360° | 2π | 1 |
Demostración
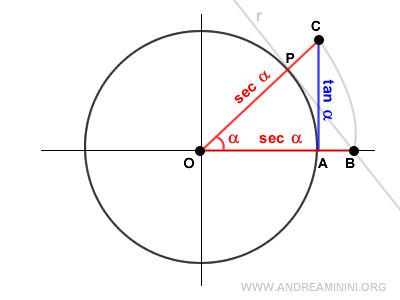
Los triángulos OAC y ODP son semejantes.
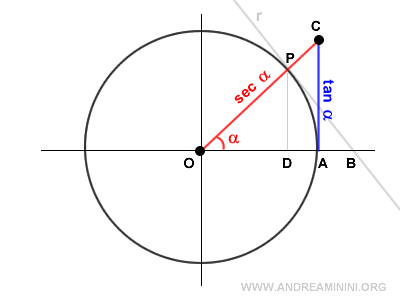
De la semejanza se deduce la siguiente proporción:
$$ \overline{OP} : \overline{OD} = \overline{OC} : \overline{OA} $$
O bien:
$$ \frac{ \overline{OP} }{ \overline{OD} } = \frac{ \overline{OC} }{ \overline{OA} } $$
El segmento \( \overline{OD} \) representa el coseno de α:
$$ \frac{1}{\cos \alpha} = \overline{OC} $$
Ya que \( OP = OA = 1 \) (radio de la circunferencia unitaria), se concluye que:
$$ \sec \alpha = \frac{1}{\cos \alpha} $$
Demostración alternativa: Los triángulos OPB y OPD también son semejantes.
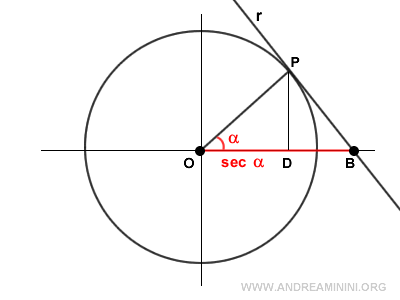
Se verifica: $$ \frac{ \overline{OD} }{ \overline{OP} } = \frac{ \overline{OP} }{ \overline{OB} } $$. Como OB representa la secante: $$ \frac{ \cos \alpha }{1} = \frac{1}{\sec \alpha} $$ y despejando se obtiene nuevamente: $$ \sec \alpha = \frac{1}{\cos \alpha} $$
Otras fórmulas de la secante
La secante también puede expresarse en función de la tangente: $$ \sec \alpha = \sqrt{1 + \tan^2 \alpha } $$ o bien: $$ \sec^2 \alpha = 1 + \tan^2 \alpha $$
Demostración
El radio, la secante y la tangente forman un triángulo rectángulo, donde la secante es la hipotenusa.
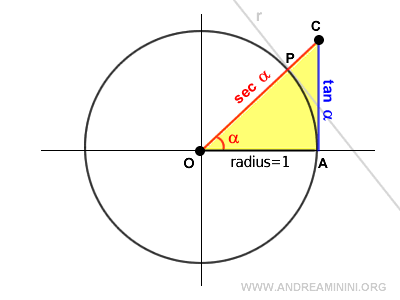
Aplicando el teorema de Pitágoras:
$$ \sec \alpha = \sqrt{1 + \tan^2 \alpha} $$
Y al elevar ambos lados al cuadrado:
$$ \sec^2 \alpha = 1 + \tan^2 \alpha $$
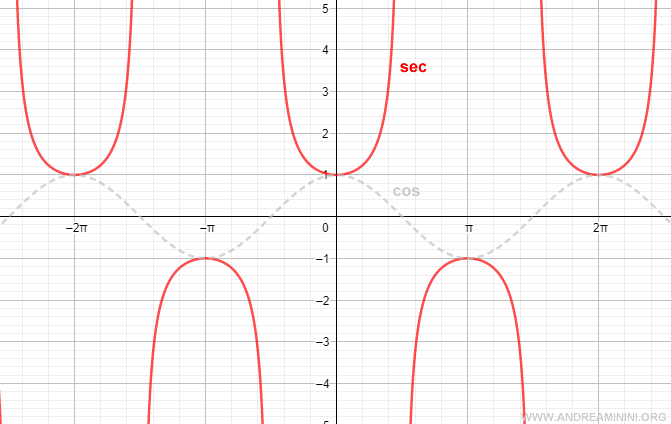
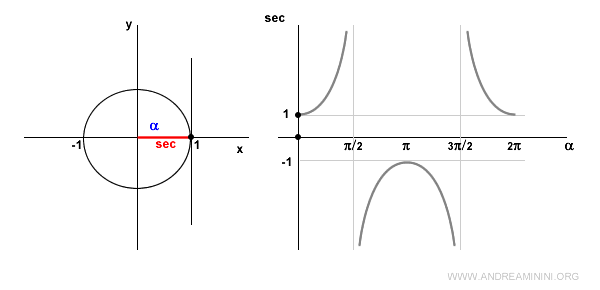
Gráfica de la secante
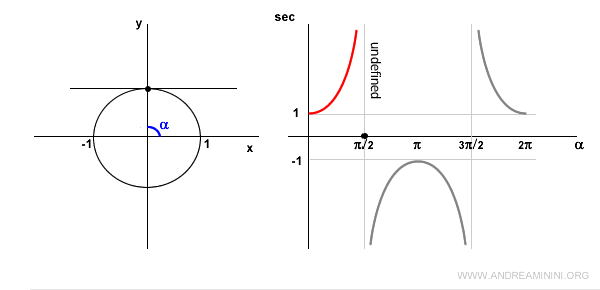
Cuando el ángulo es cero (\( \alpha = 0 \)), el coseno vale 1 y, por tanto, la secante también vale 1.
En el primer cuadrante, el coseno es positivo, así que la secante también es positiva y creciente.
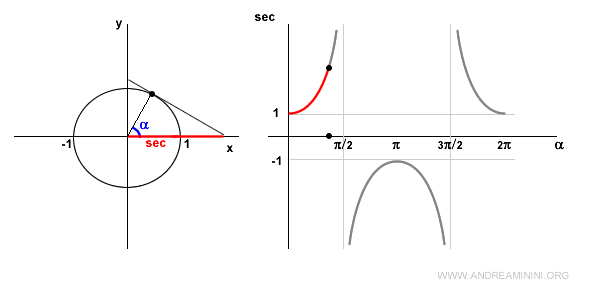
En \( \alpha = \frac{\pi}{2} \), la secante no está definida porque el coseno se anula: \( \cos(\frac{\pi}{2}) = 0 \).
En este punto, la recta tangente es paralela al eje x y no hay intersección.
En el segundo cuadrante, el coseno es negativo, por lo que la secante también lo es y sigue aumentando.
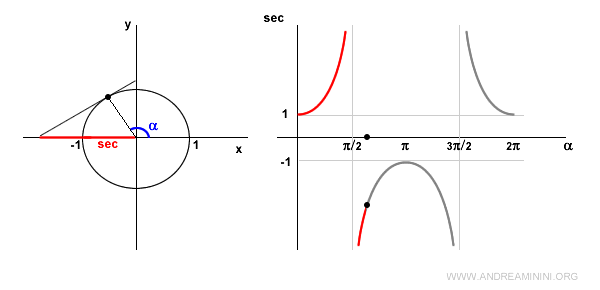
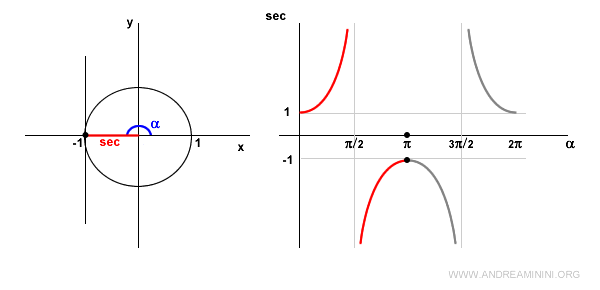
En \( \alpha = \pi \), el coseno es -1, y por tanto \( \sec(\pi) = -1 \).
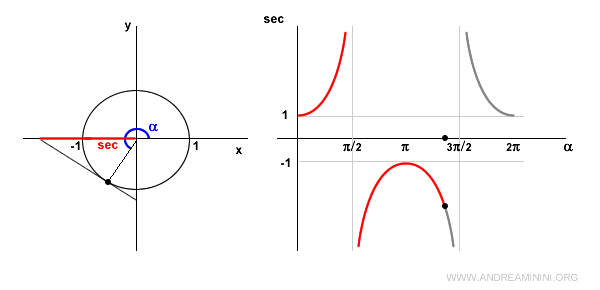
En el tercer cuadrante, el coseno sigue siendo negativo, por lo tanto la secante es negativa y decreciente.
En \( \alpha = \frac{3\pi}{2} \), el coseno vuelve a ser cero y la secante no está definida.
La tangente en ese punto es nuevamente paralela al eje x.
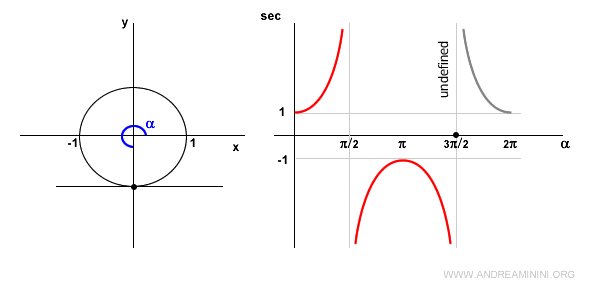
En el cuarto cuadrante, el coseno es positivo y la secante también, pero esta vez decrece.
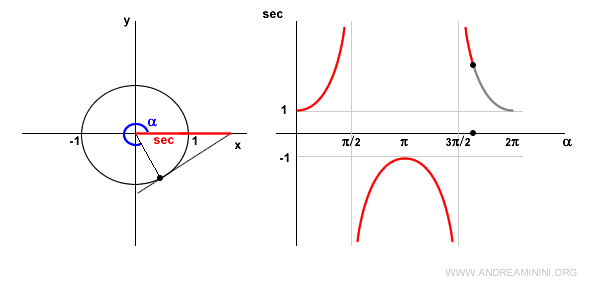
Para \( \alpha = 2\pi \), se repite el valor del ángulo cero, por lo que la secante vuelve a valer 1.
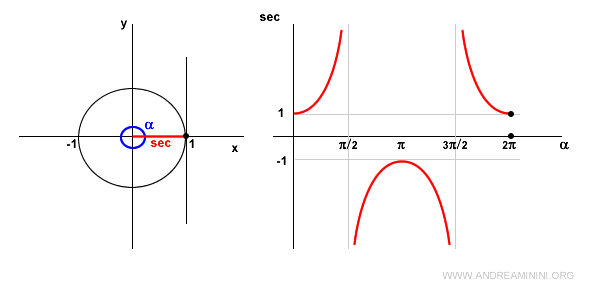
Al ser una función periódica, este comportamiento se repite cíclicamente.
Y así sucesivamente.