Entorno de un punto

Un entorno de un punto \( x_0 \) es un conjunto de puntos que se encuentran suficientemente próximos a \( x_0 \). Intuitivamente, describe qué valores están “cerca” de un punto dado.

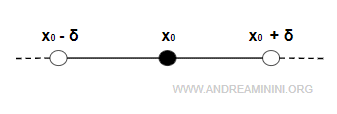
El símbolo \( \delta \) representa un número real positivo arbitrario y actúa como parámetro que determina el tamaño del entorno.

En el análisis real elemental, un entorno de un punto \( x_0 \) suele describirse mediante un conjunto de puntos $ I_0 $ que excluye los extremos del intervalo y que, según el contexto, puede incluir o no el propio punto \( x_0 \).

Por este motivo, conviene distinguir con claridad entre dos nociones relacionadas, pero conceptualmente distintas.

• Entorno perforado
  Un entorno perforado de $ x_0 $, definido para $ \delta > 0 $, es un entorno que excluye el punto $ x_0 $. Se define como la unión de dos intervalos abiertos $$  I_{ \delta } (x_0) = (x_0 - \delta, x_0)\ \cup\ (x_0, x_0 + \delta) $$
• Entorno que contiene el punto
  Un entorno de $ x_0 $ que incluye el propio punto se define, para $ \delta > 0 $, como el intervalo abierto $$  I_{ \delta } (x_0) = (x_0 - \delta, x_0 + \delta)  $$ También puede expresarse en notación conjuntista como $$ I_{ \delta } (x_0) = \{ x \in \mathbb{R} \mid  x_0 - \delta < x < x_0 + \delta \} $$ o, de forma equivalente, como $$ I_{ \delta } (x_0) = \{ x \in \mathbb{R} \mid |x-x_0| < \delta \} $$

Nota. En análisis matemático, cuando se utiliza la expresión “entorno de \( x_0 \)” sin especificaciones adicionales, casi siempre se entiende que se trata de un entorno perforado. Esta convención refleja que, en el estudio de los límites y de la continuidad, interesa el comportamiento de una función arbitrariamente cerca de un punto, y no el valor exacto de la función en dicho punto. Esta distinción es clave para un tratamiento riguroso del análisis.

Un ejemplo práctico

Supongamos que el punto x₀ es igual a diez

$$ x_0 = 10 $$

y fijamos el valor de delta en dos

$$ δ=2 $$

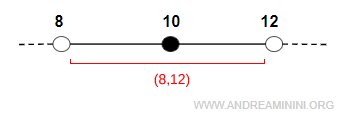
El entorno de $ x_0 $ que contiene el punto es el intervalo abierto comprendido entre ocho y doce

$$ I_0 = (x_0-δ, x_0+δ) $$

$$ I_0 = (10-2, 10+2) $$

$$ I_0 = (8, 12) $$

Se trata de un intervalo abierto que incluye todos los números reales estrictamente mayores que ocho y estrictamente menores que doce. Como el entorno se ha definido para contener el punto, el valor $ x_0 = 10 $ pertenece a este conjunto.

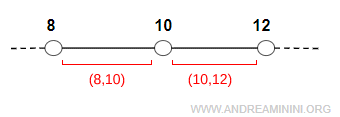
Por el contrario, el entorno perforado de $ 10 $ no incluye el punto \( x_0 = 10 \). No es un único intervalo abierto, sino la unión de dos intervalos abiertos disjuntos:

$$ I_0 = (x_0 - \delta, x_0)\ \cup\ (x_0, x_0 + \delta) $$

$$ I_0 = (10 - 2, 10)\ \cup\ (10, 10 + 2) $$

$$ I_0 = (8, 10)\ \cup\ (10, 12) $$

En este caso, el punto $ x_0 = 10 $ no pertenece al entorno.

Nota. Salvo que se indique explícitamente lo contrario, un entorno no tiene por qué ser simétrico respecto de $ x_0 $. Por ejemplo, puede definirse un entorno utilizando dos números reales positivos distintos $ \delta_1 \ne \delta_2 $ como $$ (x_0-δ_1, x_0+δ_2) $$ En este caso, el punto $ x_0 $ deja de ser el punto medio del intervalo. Algunos manuales denominan al caso simétrico $ \delta_1 = \delta_2 $ entorno de radio $ \delta $. En el contexto de $ \mathbb{R}^2 $ también se utiliza el término “entorno circular” para describir entornos en el plano. Para evitar ambigüedades, aquí se reservan los términos “entorno” y “entorno perforado” para puntos de la recta real, mientras que entorno circular se emplea para los entornos en el plano.

Entornos derecho e izquierdo

En muchas situaciones prácticas resulta útil analizar el comportamiento de una función restringiendo la atención a los puntos situados exclusivamente a la derecha o a la izquierda de un punto dado.

De esta necesidad surgen de manera natural las nociones de entorno derecho y entorno izquierdo.

• Entorno derecho
  El entorno derecho de un punto \( x_0 \), denotado por \( I_0^+ \), es el conjunto de números reales mayores que \( x_0 \) y contenidos en el intervalo abierto $ ( x_0, x_0+ \delta ) $, con \( \delta > 0 \). $$ I_0^+ = (x_0, x_0 + \delta) $$
• Entorno izquierdo
  El entorno izquierdo de un punto \( x_0 \), denotado por \( I_0^- \), es el conjunto de números reales menores que \( x_0 \) y contenidos en el intervalo abierto $ ( x_0- \delta, x_0 ) $, con \( \delta > 0 \). $$ I_0^- = (x_0 - \delta, x_0) $$

Estas nociones son fundamentales en el estudio de los límites laterales y en el análisis de la continuidad de una función.

Por ejemplo, si \( x_0 = 2 \) y \( \delta = 0.5 \), el entorno derecho es \[ I_0^+ = (2, 2.5) \] mientras que el entorno izquierdo es \[ I_0^- = (1.5, 2) \]

Entorno del infinito

En determinados contextos resulta útil considerar intervalos abiertos que no están acotados ni superior ni inferiormente.

A estos conjuntos se los denomina entornos del infinito.

• Entorno de menos infinito
  Un entorno de menos infinito es el intervalo abierto no acotado inferiormente que contiene todos los números reales menores que un número real fijo \( a \).  \[ I(-\infty) = (-\infty, a) = \{ x \in \mathbb{R} \mid x < a \} \]
• Entorno de más infinito
  Un entorno de más infinito es el intervalo abierto no acotado superiormente que contiene todos los números reales mayores que un número real fijo \( a \). \[ I(+\infty) = (a, +\infty) = \{ x \in \mathbb{R} \mid x > a \} \]

Siempre que se utilice el símbolo de infinito, debe indicarse de forma explícita su signo, ya que el símbolo genérico \( \infty \) puede referirse tanto a \( -\infty \) como a \( +\infty \).

Por ejemplo, si \( a = 3 \), un entorno de menos infinito es \[ I(-\infty) = (-\infty, 3) \] mientras que un entorno de más infinito es \[ I(+\infty) = (3, +\infty) \] En términos numéricos, el número \( -1000 \) pertenece al entorno de menos infinito, mientras que el número \( 10 \) pertenece al entorno de más infinito.

Notas

Observaciones adicionales sobre los entornos

• La intersección y la unión de dos entornos de $ x_0 $ son, a su vez, entornos de $ x_0 $

Y así sucesivamente.