Límites laterales de una función

Cuando analizamos una función, el comportamiento cerca de un punto puede observarse desde dos direcciones distintas. Si nos acercamos a x₀ desde valores mayores que x₀, hablamos del límite lateral derecho:
$$ \lim_{x \rightarrow x_0^+} f(x) $$ En cambio, si nos aproximamos desde valores menores, hablamos del límite lateral izquierdo:
$$ \lim_{x \rightarrow x_0^-} f(x) $$

Estos límites describen cómo se comporta la función al aproximarse a un punto, y pueden ser finitos o tender al infinito. En algunos casos, la función no posee ninguno de los dos, lo que indica una discontinuidad en ese punto.

Ejemplo. La función logarítmica f(x) = log(x) solo está definida para valores positivos de x, es decir, x ∈ (0, +∞). Por eso, el límite cuando x tiende a 0 solo puede considerarse por la derecha, cuando x → 0⁺. No existe límite lateral izquierdo porque la función no está definida para valores negativos.

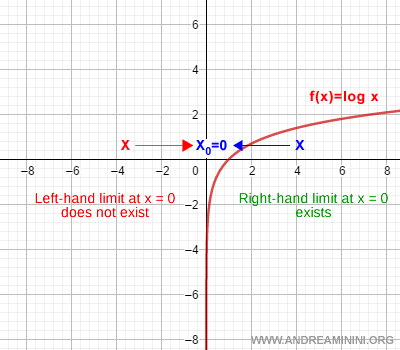
Límite lateral derecho

Decimos que el límite lateral derecho de una función f(x) cuando x → x₀⁺ es igual a l si, para todo ε > 0, existe un δ > 0 tal que |f(x) - l| < ε siempre que x esté dentro del intervalo (x₀, x₀ + δ):
$$ \lim_{x \rightarrow x_0^+} f(x) = l $$

En notación formal:

$$ \lim_{x \rightarrow x_0^+} f(x) = l \Leftrightarrow \forall \epsilon>0, \exists \delta>0: |f(x)-l|<\epsilon, \forall x \in (x_0, x_0+\delta) $$

Observación. Este tipo de límite también puede entenderse mediante sucesiones. Si tomamos una sucesión x_n que se aproxima a x₀ por la derecha, los valores de f(x_n) deben acercarse a l a medida que n crece.

Ejemplo

Consideremos la función f(x) = 1/x, que no está definida en x = 0:

$$ f(x) = \frac{1}{x} $$

Analizamos su comportamiento cuando x se aproxima a 0 por la derecha, sin llegar a tocar el punto:

$$ \lim_{x \rightarrow 0^+} \frac{1}{x} $$

El límite lateral derecho existe y es igual a +∞:

$$ \lim_{x \rightarrow 0^+} \frac{1}{x} = +\infty $$

Gráficamente, esto significa que la función crece sin límite al acercarse al eje y desde la derecha:

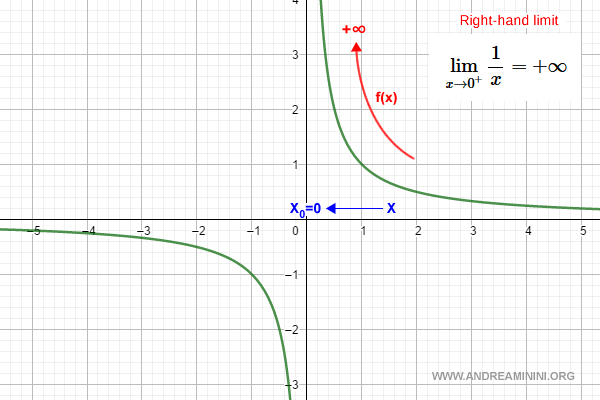
Límite lateral izquierdo

De manera análoga, el límite lateral izquierdo de una función f(x) cuando x → x₀^- es igual a l si, para todo ε > 0, existe un δ > 0 tal que |f(x) - l| < ε para todo x dentro del intervalo (x₀ - δ, x₀):
$$ \lim_{x \rightarrow x_0^-} f(x) = l $$

En forma simbólica:

$$ \lim_{x \rightarrow x_0^-} f(x) = l \Leftrightarrow \forall \epsilon>0, \exists \delta>0: |f(x)-l|<\epsilon, \forall x \in (x_0-\delta, x_0) $$

Observación. También puede expresarse con sucesiones: si una sucesión x_n se aproxima a x₀ desde la izquierda, los valores f(x_n) deben acercarse a l conforme n aumenta.

Ejemplo

Consideremos nuevamente la función f(x) = 1/x, no definida en x = 0:

$$ f(x) = \frac{1}{x} $$

Calculamos ahora el límite cuando x se aproxima a 0 por la izquierda:

$$ \lim_{x \rightarrow 0^-} \frac{1}{x} $$

En este caso, el límite lateral izquierdo existe y es igual a -∞:

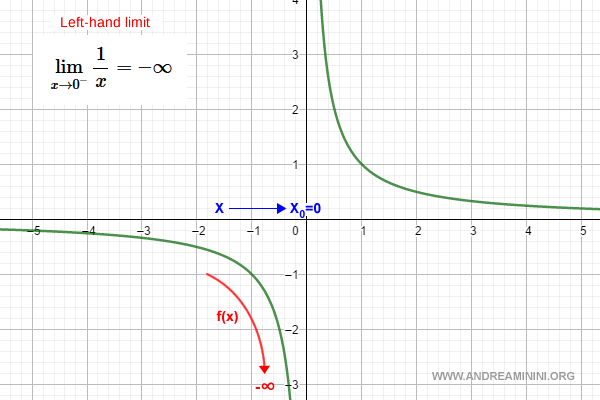
$$ \lim_{x \rightarrow 0^-} \frac{1}{x} = -\infty $$

Observación. El resultado es negativo porque al aproximarse a cero desde la izquierda, los valores de x son negativos (por ejemplo, x = -0.3, x = -0.1, x = -0.01), lo que hace que 1/x tome valores cada vez más grandes en magnitud pero negativos.

En el plano cartesiano, la gráfica se muestra así:

Comprender los límites laterales es esencial para estudiar la continuidad de una función y detectar puntos de salto o de divergencia. Son una herramienta básica en el análisis matemático, pero también una de las más útiles para interpretar el comportamiento real de las funciones en su entorno inmediato.

Un ejemplo completamente desarrollado

Analicemos paso a paso un ejemplo concreto a partir de la siguiente función definida por tramos.

\[
f(x)=
\begin{cases}
x^2 & \text{si } x<2 \\ \\
4x-4 & \text{si } x\ge 2
\end{cases}
\]

Límite lateral derecho

Empezamos estudiando el límite lateral derecho en el punto \( x=2 \).

\[ \lim_{x\to 2^+} f(x)=4 \]

Dado que se trata de un límite por la derecha, solo consideramos valores de \( x \) mayores que 2.

En ese intervalo, y para valores suficientemente cercanos a 2, la función coincide con el segundo tramo:

\[ f(x)=4x-4 \]

Por definición, decir que \( f(x) \) tiende a 4 cuando \( x\to 2^+ \) significa que, para todo \( \varepsilon>0 \), existe un entorno lateral derecho de 2 tal que

\[ |f(x)-4|<\varepsilon \]

para todos los valores de \( x \) contenidos en dicho entorno.

Sustituyendo la expresión de la función, obtenemos

\[ |(4x-4)-4|<\varepsilon \]

que se simplifica en

\[ |4x-8|<\varepsilon \]

Aplicando la propiedad básica del valor absoluto,

\[ |A|<\varepsilon \quad \Longleftrightarrow \quad -\varepsilon<A<\varepsilon \]

y tomando \( A=4x-8 \), resulta

\[ -\varepsilon<4x-8<\varepsilon \]

Sumando 8 en todos los términos se obtiene

\[ 8-\varepsilon<4x<8+\varepsilon \]

y, al dividir entre 4,

\[ 2-\frac{\varepsilon}{4}<x<2+\frac{\varepsilon}{4} \]

Como solo nos interesan los valores mayores que 2, nos quedamos con

\[ 2<x<2+\frac{\varepsilon}{4} \]

Este intervalo define un entorno lateral derecho de 2.

Si expresamos la condición en términos de \( \delta \), basta elegir \( \delta=\frac{\varepsilon}{4} \). Así,

\[ 2<x<2+\delta \]

o, de forma equivalente,

\[ 0<x-2<\delta \]

lo que garantiza que

\[ 0<x-2<\delta \quad \Longrightarrow \quad |f(x)-4|<\varepsilon \]

Dado que este razonamiento vale para cualquier \( \varepsilon>0 \), concluimos que

\[ \lim_{x\to 2^+} f(x)=4 \]

Límite lateral izquierdo

Pasemos ahora al estudio del límite lateral izquierdo en el mismo punto.

\[
f(x)=
\begin{cases}
x^2 & \text{si } x<2 \\ \\
4x-4 & \text{si } x\ge 2
\end{cases}
\]

Queremos comprobar que

\[ \lim_{x\to 2^-} f(x)=4 \]

En este caso nos restringimos a valores de \( x \) menores que 2.

En un entorno lateral izquierdo de 2, la función viene dada por

\[ f(x)=x^2 \]

Según la definición de límite, \( f(x) \) tiende a 4 cuando \( x\to 2^- \) si, para todo \( \varepsilon>0 \), se cumple

\[ |f(x)-4|<\varepsilon \]

siempre que \( x \) esté suficientemente cerca de 2 por la izquierda.

Sustituyendo la expresión de la función, obtenemos

\[ |x^2-4|<\varepsilon \]

Esta diferencia de cuadrados puede factorizarse como

\[ |x^2-4|=|(x-2)(x+2)|=|x-2|\cdot|x+2| \]

La condición queda entonces

\[ |x-2|\cdot|x+2|<\varepsilon \]

Para controlar el factor \( |x+2| \), restringimos \( x \) a un entorno lateral izquierdo sencillo, por ejemplo

\[  1<x<2 \]

Sumando 2 en cada término se obtiene

\[  3<x+2<4 \]

y, por tanto,

\[ |x+2|<4 \]

Esta cota nos permite simplificar la estimación. En efecto, si \(|x+2|<4 \), entonces

\[ |x-2|\cdot|x+2|<4|x-2| \]

Por consiguiente, basta exigir

\[ 4|x-2|<\varepsilon \]

lo que equivale a

\[ |x-2|<\frac{\varepsilon}{4} \]

Además, para mantenernos a la izquierda de 2, imponemos la condición \( x<2 \).

La desigualdad \(|x-2|<\varepsilon/4 \) es equivalente a

\[ -\frac{\varepsilon}{4}<x-2<\frac{\varepsilon}{4} \]

Sumando 2 en todos los términos se obtiene

\[ 2-\frac{\varepsilon}{4}<x<2+\frac{\varepsilon}{4} \]

Al combinar esta condición con \( x<2 \), resulta finalmente

\[ 2-\frac{\varepsilon}{4}<x<2 \]

Este intervalo define un entorno lateral izquierdo de 2.

En consecuencia, si $ x $ está suficientemente cerca de 2 por la izquierda, entonces $ x^2 $ está suficientemente cerca de 4.

\[ \lim_{x\to 2^-} f(x)=4 \]

Por lo tanto, el límite lateral izquierdo también vale 4.

Y así sucesivamente.