Teorema de Bolzano-Weierstrass

Toda sucesión acotada a_n contiene al menos una subsucesión convergente.

Este resultado garantiza que, incluso dentro de una sucesión que oscila o parece desordenada, siempre es posible encontrar un núcleo ordenado que converge hacia un valor concreto.

Demostración

Si una sucesión está acotada, existen dos números reales a y b tales que:

$$ a \le a_n \le b $$

Los valores a y b actúan como cota inferior y cota superior de la sucesión.

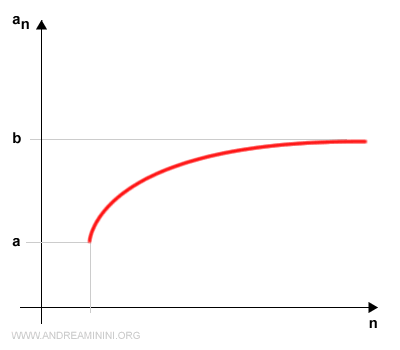
Estas cotas determinan un intervalo cerrado que contiene todos los términos a_n en el eje vertical (eje y).

En el eje horizontal (eje x) representamos el índice n de la sucesión.

Nota. Una sucesión a_n posee infinitos términos porque su índice n recorre los números naturales, que constituyen un conjunto infinito.

Dividimos el intervalo [a, b] en dos partes iguales mediante el punto medio \( c = (a+b)/2 \).

De este modo obtenemos dos subintervalos: [a, c] y [c, b].

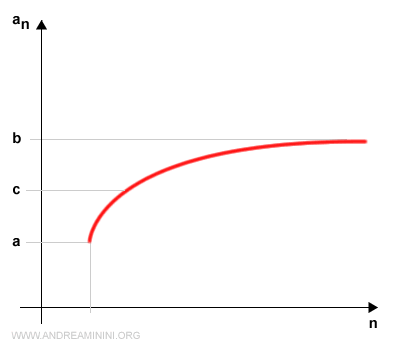
Uno y solo uno de estos dos subintervalos contendrá infinitos términos de la sucesión, mientras que el otro contendrá a lo sumo un número finito.

Supondremos, sin pérdida de generalidad, que el intervalo [c, b] contiene infinitos términos.

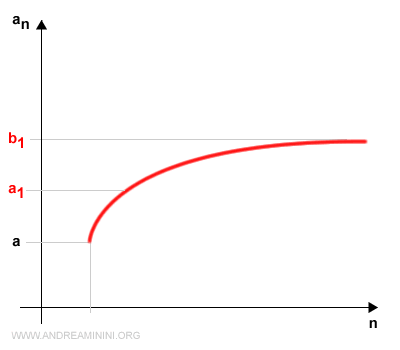
Renombramos dicho intervalo como [a₁, b₁]:

$$ [c, b] = [a_1, b_1] $$

De inmediato se verifican las desigualdades:

$$ a \le a_1 $$ $$ b_1 \le b $$

y la longitud del nuevo intervalo es exactamente la mitad de la longitud inicial:

$$ b_1 - a_1 = \frac{b - a}{2} $$

Llamemos n₁ al menor índice de la sucesión cuyo término pertenece al intervalo [a₁, b₁].

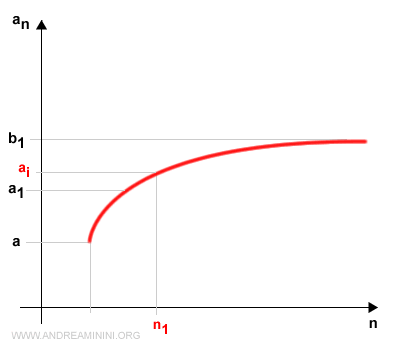
Volvemos a dividir el intervalo [a₁, b₁] en dos partes iguales: [a₁, c₁] y [c₁, b₁].

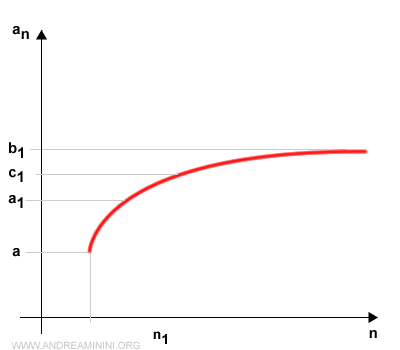
Una vez más, uno y solo uno de estos subintervalos contendrá infinitos términos.

Supondremos que el intervalo [c₁, b₁] es el que contiene infinitos términos.

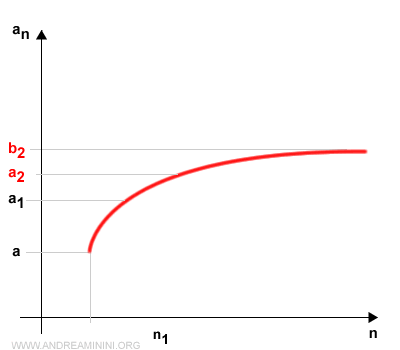
Renombramos este subintervalo como [a₂, b₂]:

$$ [c_1, b_1] = [a_2, b_2] $$

y se verifican las nuevas desigualdades:

$$ a_1 \le a_2 $$ $$ b_2 \le b_1 $$

y la longitud queda reducida nuevamente a la mitad:

$$ b_2 - a_2 = \frac{b_1 - a_1}{2} = \frac{b - a}{4} $$

Sea n₂ el menor índice tal que a_n2 pertenece a [a₂, b₂]. Por construcción, n₂ es estrictamente mayor que n₁.

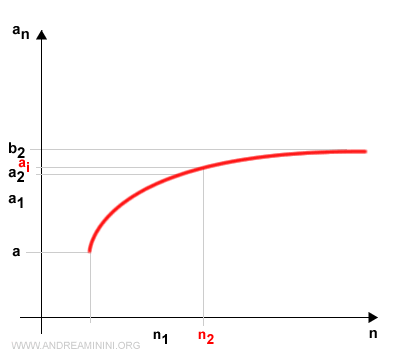
Iterando este procedimiento k veces, obtenemos tras k pasos la cadena:

$$ a \le a_k \le b_k \le b $$

La longitud del intervalo [a_k, b_k] es:

$$ b_k - a_k = \frac{b - a}{2^k} $$

Sea n_k el menor índice tal que a_nk pertenece a [a_k, b_k]. Cada n_k es estrictamente mayor que el anterior n_k-1, por lo que obtenemos una sucesión estrictamente creciente de índices:

$$ n_1, n_2, \dots, n_{k-1}, n_k $$

Todos estos índices son números naturales y cumplen:

$$ n_1 < n_2 < \dots < n_{k-1} < n_k $$

A partir de ellos se obtiene una subsucesión:

$$ a_{n_1}, a_{n_2}, \dots, a_{n_k} $$

y cada término cumple:

$$ a_{n_k} \in [a_k, b_k] $$

por lo que:

$$ a_k \le a_{n_k} \le b_k $$

Así se construyen tres sucesiones:

• la sucesión de cotas inferiores a_k,
• la subsucesión a_nk,
• y la sucesión de cotas superiores b_k.

Las sucesiones a_k y b_k son monótonas y acotadas, y satisfacen:

$$ a \le a_1 \le a_2 \le \dots \le a_k \le b_1 \le b_2 \le \dots \le b_k \le b $$

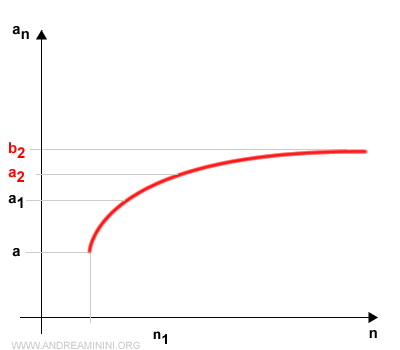
Al tomar límites cuando k → ∞, se obtiene:

$$ \lim_{k \rightarrow \infty;} a_k \le \lim_{k \rightarrow \infty;} a_{n_k} \le \lim_{k \rightarrow \infty;} b_k $$

Como a_k y b_k son monótonas y acotadas, el Teorema de Convergencia Monótona garantiza la existencia de dos límites finitos:

$$ l_1 \le \lim_{k \rightarrow \infty;} a_{n_k} \le l_2 $$

En realidad, ambos límites coinciden, es decir, l₁ = l₂:

$$ l \le \lim_{k \rightarrow \infty;} a_{n_k} \le l $$

Explicación. Como $$ b_k - a_k = \frac{b - a}{2^k} $$ se tiene $$ b_k = a_k + \frac{b - a}{2^k} $$ y por tanto:

$$ l_2 = \lim_{k \rightarrow \infty;} b_k = \lim_{k \rightarrow \infty;} \left(a_k + \frac{b-a}{2^k}\right) = \lim_{k \rightarrow \infty;} a_k + \lim_{k \rightarrow \infty;} \frac{b-a}{2^k} = l_1 $$

porque \((b-a)/2^k\) tiende a cero cuando k crece indefinidamente.

Aplicando ahora el Teorema del Sándwich, la subsucesión a_nk converge también al mismo límite finito l:

$$ \lim_{k \rightarrow \infty;} a_{n_k} = l $$

Por tanto, la subsucesión a_nk es convergente.

Con esto queda demostrada la validez del Teorema de Bolzano-Weierstrass.