Operaciones con límites

Los límites pueden sumarse, restarse, multiplicarse o dividirse. Las reglas que siguen son válidas tanto para los límites de sucesiones como para los de funciones.

Suma y resta de límites

Si se tienen dos sucesiones con límite cuando n → ∞: $$ \lim_{n \rightarrow +\infty } a_n = l_1 \\ \lim_{n \rightarrow +\infty } b_n = l_2 $$ donde l₁ y l₂ son números reales, entonces: $$ \lim_{n \rightarrow +\infty } \bigl( a_n + b_n \bigr) = l_1 + l_2 $$ y, de manera análoga: $$ \lim_{n \rightarrow +\infty } \bigl( a_n - b_n \bigr) = l_1 - l_2 $$

Ejemplo

Consideremos dos sucesiones cuyos límites tienden a +1 y +2, respectivamente:

$$ \lim_{n \rightarrow +\infty } \frac{n+1}{n} = 1 \\ \lim_{n \rightarrow +\infty } \frac{2n-1}{n} = 2 $$

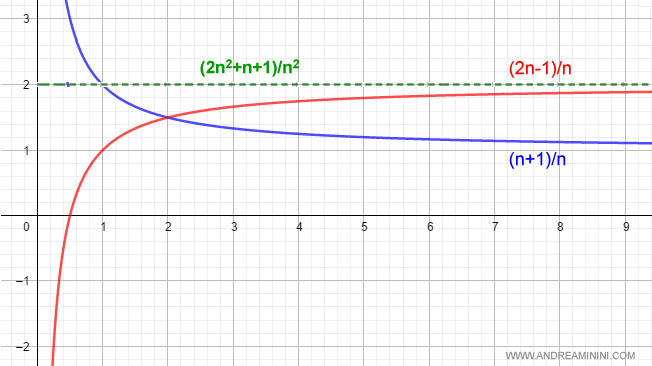
Su representación gráfica es la siguiente:

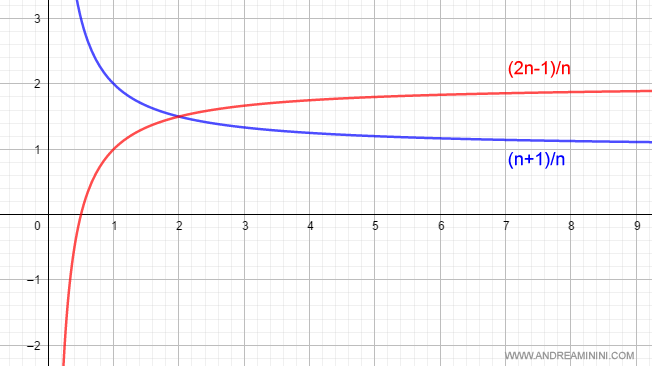
La suma de estos dos límites es 3:

$$ \lim_{n \rightarrow +\infty } \frac{n+1}{n} + \lim_{n \rightarrow +\infty } \frac{2n-1}{n} = 1 + 2 = 3 $$

Comprobemos este resultado directamente:

$$ \lim_{n \rightarrow +\infty } \left( \frac{n+1}{n} + \frac{2n-1}{n} \right) $$

$$ \lim_{n \rightarrow +\infty } \frac{n+1+2n-1}{n} $$

$$ \lim_{n \rightarrow +\infty } \frac{3n}{n} = 3 $$

Como era de esperar, el resultado coincide.

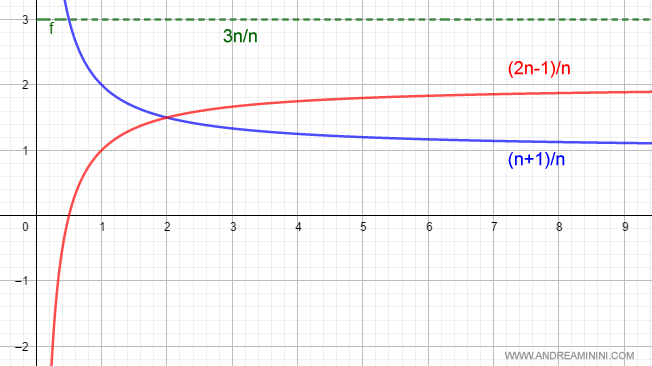
En conclusión, el límite de una suma es igual a la suma de los límites de las sucesiones o funciones implicadas.

Demostración

Para todo ε > 0, existe un valor v₁ tal que:

$$ \forall \epsilon > 0 \; \exists \; v_1 : |a_n - l_1| < \epsilon, \; \forall n > v_1 $$

La misma propiedad vale para la segunda sucesión:

$$ \forall \epsilon > 0 \; \exists \; v_2 : |b_n - l_2| < \epsilon, \; \forall n > v_2 $$

Ejemplo

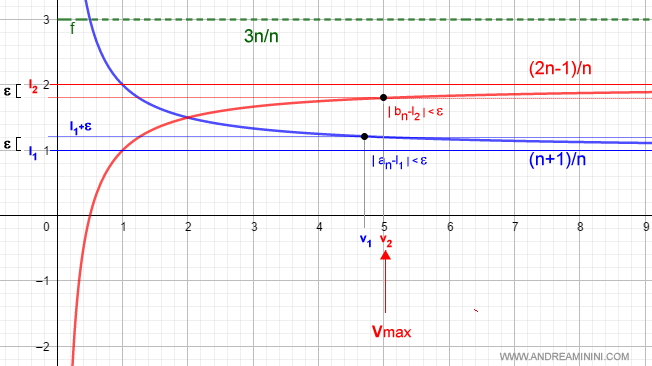
Tomamos el máximo entre v₁ y v₂:

De este modo nos aseguramos de que ambas condiciones se cumplan a la vez para todo n > v:

$$ v = \max(v_1, v_2) $$

Ejemplo. En el caso anterior, la condición para la primera sucesión (azul) era n > 4.7, mientras que para la segunda (roja) era n > 5. Por lo tanto, a partir de n > 5 se cumplen ambas condiciones.

Así, para todo n > v, la suma de las dos sucesiones verifica:

$$ |(a_n + b_n) - (l_1 + l_2)| < 2\epsilon $$

Reescribimos el valor absoluto de la siguiente forma:

$$ |(a_n - l_1) + (b_n - l_2)| < 2\epsilon $$

Aplicando la desigualdad triangular obtenemos:

$$ |(a_n - l_1) + (b_n - l_2)| \le |a_n - l_1| + |b_n - l_2| $$

Como: $$ |a_n - l_1| < \epsilon \\ |b_n - l_2| < \epsilon $$

se sigue que: $$ |(a_n - l_1) + (b_n - l_2)| < \epsilon + \epsilon = 2\epsilon $$

De este modo queda demostrada la igualdad entre el límite de la suma y la suma de los límites de las sucesiones o funciones consideradas.

Producto de dos límites

Si se tienen dos sucesiones con límite cuando n → ∞: $$ \lim_{n \rightarrow +\infty } a_n = l_1 \\ \lim_{n \rightarrow +\infty } b_n = l_2 $$ donde l₁ y l₂ son números reales, entonces: $$ \lim_{n \rightarrow +\infty } \bigl( a_n \cdot b_n \bigr) = \lim_{n \rightarrow +\infty } a_n \cdot \lim_{n \rightarrow +\infty } b_n = l_1 \cdot l_2 $$

Ejemplo

Consideremos dos sucesiones que convergen a +1 y +2, respectivamente:

$$ \lim_{n \rightarrow +\infty } \frac{n+1}{n} = 1 \\ \lim_{n \rightarrow +\infty } \frac{2n-1}{n} = 2 $$

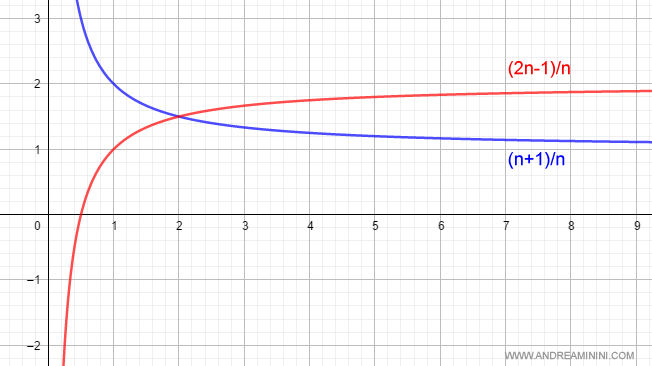
Gráficamente se obtiene lo siguiente:

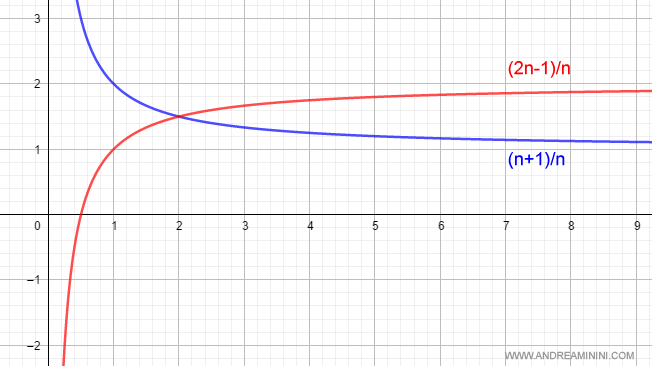
Según la regla, el producto de estos límites es 2:

$$ \lim_{n \rightarrow +\infty } \frac{n+1}{n} \cdot \lim_{n \rightarrow +\infty } \frac{2n-1}{n} = 1 \cdot 2 = 2 $$

Verifiquémoslo directamente:

$$ \lim_{n \rightarrow +\infty } \left( \frac{n+1}{n} \cdot \frac{2n-1}{n} \right) $$

$$ \lim_{n \rightarrow +\infty } \frac{(n+1)\cdot(2n-1)}{n^2} $$

$$ \lim_{n \rightarrow +\infty } \frac{2n^2 + n - 1}{n^2} = \frac{\infty}{\infty} $$

Como se trata de una forma indeterminada ∞/∞, aplicamos la Regla de L’Hôpital:

$$ \lim_{n \rightarrow +\infty } \frac{2n^2 + n - 1}{n^2} = \lim_{n \rightarrow +\infty } \frac{4n + 1}{2n} = \lim_{n \rightarrow +\infty } \frac{4}{2} = 2 $$

Y el resultado concuerda perfectamente.

En conclusión, el límite de un producto es igual al producto de los límites de las sucesiones o funciones correspondientes.

Cociente de dos límites

Si se tienen dos sucesiones con límite cuando n → ∞: $$ \lim_{n \rightarrow +\infty } a_n = l_1 \\ \lim_{n \rightarrow +\infty } b_n = l_2 $$ donde l₁ y l₂ son números reales, entonces el límite de su cociente es: $$ \lim_{n \rightarrow +\infty } \frac{a_n}{b_n} = \frac{\lim_{n \rightarrow +\infty } a_n}{\lim_{n \rightarrow +\infty } b_n} = \frac{l_1}{l_2} $$ siempre que \( l_2 \neq 0 \).

Ejemplo

Consideremos dos sucesiones que convergen a +1 y +2, respectivamente:

$$ \lim_{n \rightarrow +\infty } \frac{n+1}{n} = 1 \\ \lim_{n \rightarrow +\infty } \frac{2n-1}{n} = 2 $$

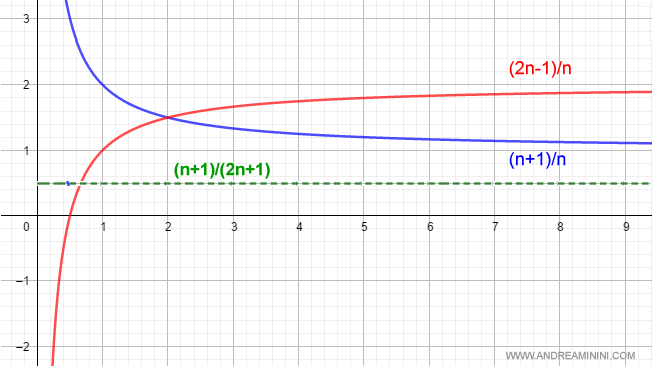
Gráficamente se representa así:

De acuerdo con la regla, el cociente de estos límites es:

$$ \frac{\lim_{n \rightarrow +\infty } \frac{n+1}{n}}{\lim_{n \rightarrow +\infty } \frac{2n-1}{n}} = \frac{1}{2} $$

Verifiquémoslo directamente:

$$ \lim_{n \rightarrow +\infty } \frac{\frac{n+1}{n}}{\frac{2n-1}{n}} $$

$$ \lim_{n \rightarrow +\infty } \frac{n+1}{n} \cdot \frac{n}{2n-1} $$

$$ \lim_{n \rightarrow +\infty } \frac{n+1}{2n-1} = \frac{\infty}{\infty} $$

Al ser una forma indeterminada ∞/∞, aplicamos la Regla de L’Hôpital:

$$ \lim_{n \rightarrow +\infty } \frac{1}{2} = \frac{1}{2} $$

Y, efectivamente, el resultado es correcto.

En consecuencia, el límite de un cociente es igual al cociente de los límites de las sucesiones o funciones, siempre que el límite del denominador no sea nulo.

Y así sucesivamente.