Límite del producto de una sucesión acotada y otra que tiende a cero
En matemáticas, hay un resultado muy útil que conecta dos ideas básicas: las sucesiones acotadas y las sucesiones que tienden a cero. Si una sucesión an está acotada y otra bn converge a cero, entonces el producto de ambas también se aproxima a cero. $$ \lim_{n \rightarrow \infty } a_n \cdot b_n = 0 $$
Un ejemplo para entenderlo mejor
Veamos el caso de estas dos sucesiones:
$$ a_n = \frac{n+1}{n} $$
$$ b_n = \frac{1}{n} $$
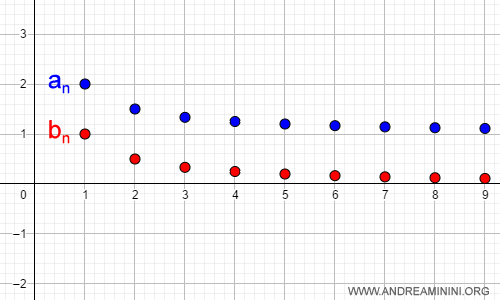
La primera, an, es acotada (no crece indefinidamente), mientras que la segunda, bn, tiende a cero cuando n aumenta.
$$ \lim_{n \rightarrow \infty } a_n = 1 \qquad \text{y} \qquad \lim_{n \rightarrow \infty } b_n = 0 $$
Recuerda: decimos que una sucesión está acotada si existe un número M>0 tal que |an|<M para todo n>0. En cambio, una sucesión tiende a cero si sus términos se aproximan cada vez más a 0 cuando n crece.
Si multiplicamos ambas sucesiones, el resultado también se acerca a cero:
$$ \lim_{n \rightarrow \infty } a_n \cdot b_n = 1 \cdot 0 = 0 $$
Veamos paso a paso cómo se obtiene este resultado.
Primero calculamos el producto:
$$ a_n \cdot b_n = \frac{n+1}{n} \cdot \frac{1}{n} = \frac{n+1}{n^2} $$
Si tomamos el límite cuando n tiende a infinito:
$$ \lim_{n \rightarrow \infty } \frac{n+1}{n^2} = \frac{\infty}{\infty} $$
Es una forma indeterminada. Para resolverla, aplicamos la Regla de L’Hôpital:
$$ \lim_{n \rightarrow \infty } \frac{D[n+1]}{D[n^2]} = \lim_{n \rightarrow \infty } \frac{1}{2n} = 0 $$
Así comprobamos que el producto efectivamente tiende a cero.
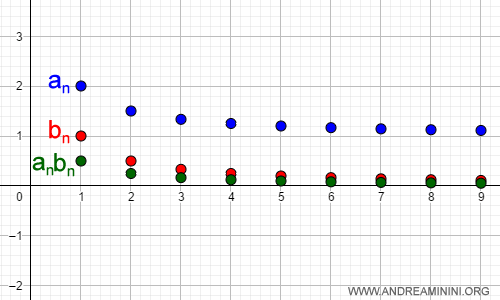
¿Por qué ocurre esto?
La razón es sencilla pero elegante. Si una sucesión an está acotada, existe un número M>0 tal que:
$$ | a_n | \le M $$
Si multiplicamos ambos lados por |bn|, obtenemos:
$$ | a_n | \cdot |b_n| \le M \cdot |b_n| $$
Esto significa que el producto an·bn está “encajonado” entre -M|bn| y M|bn|:
$$ -M \cdot |b_n| \le a_n \cdot b_n \le M \cdot |b_n| $$
Y como bn tiende a cero, los dos extremos del encajonamiento también lo hacen:
$$ -M \cdot |0| \le a_n \cdot b_n \le M \cdot 0 $$
Por el Teorema del Encajonamiento, el producto debe converger a cero.
Este resultado es fundamental en análisis matemático: muestra cómo el comportamiento de una sucesión puede dominar al de otra, y cómo el límite de un producto puede ser determinado incluso cuando una de las partes no converge por sí sola.
Una lección sencilla, pero con un alcance profundo.