Teorema de la Conservación del Signo en el Límite de una Función

El teorema de la conservación del signo establece que si una función continua toma un valor positivo en un punto, entonces también será positiva en un entorno cercano a ese punto. En otras palabras, la continuidad garantiza que el signo de la función no cambia bruscamente alrededor de ese valor.

Ejemplo

Veamos un ejemplo sencillo con la función:

$$ f(x) = \frac{1}{x} $$

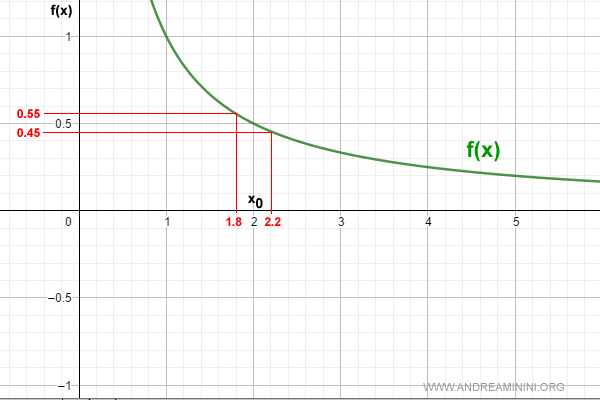
En el punto x₀ = 2, la función vale:

$$ f(2) = 0.5 $$

Tomemos un entorno alrededor de x₀ con δ = 0.2:

$$ (x_0 - \delta, \, x_0 + \delta) = (1.8, \, 2.2) $$

En este intervalo, la función sigue siendo positiva para todos los valores de x:

$$ f(1.8) = \frac{1}{1.8} = 0.55, \quad f(2.2) = \frac{1}{2.2} = 0.45 $$

Podemos comprobar que, aunque los valores de la función cambian ligeramente, el signo se mantiene constante.

Observación. Si f(x₀) > 0, siempre existe un número δ > 0 tal que f(x) > 0 para todo x dentro del intervalo (x₀ - δ, x₀ + δ). Lo mismo se cumple si f(x₀) < 0: la función será negativa en un entorno de x₀.

Demostración

La idea es sencilla, pero el razonamiento matemático que la respalda es riguroso. Supongamos que la función es continua y positiva en el punto x₀:

$$ f(x_0) > 0 $$

Tomamos un valor pequeño, por ejemplo:

$$ \epsilon = \frac{f(x_0)}{2} $$

Por la definición de límite, la continuidad garantiza que existe un δ > 0 tal que, para todo x suficientemente próximo a x₀, se cumple:

$$ |f(x) - f(x_0)| < \epsilon $$

De esta desigualdad obtenemos:

$$ -\frac{f(x_0)}{2} < f(x) - f(x_0) < \frac{f(x_0)}{2} $$

Si sumamos f(x₀) en todos los términos, resulta:

$$ f(x_0) - \frac{f(x_0)}{2} < f(x) < f(x_0) + \frac{f(x_0)}{2} $$

Lo que equivale a:

$$ \frac{f(x_0)}{2} < f(x) < \frac{3f(x_0)}{2} $$

Como f(x₀) > 0, el término f(x₀)/2 también es positivo. Por tanto, f(x) se mantiene estrictamente positiva dentro del entorno (x₀ - δ, x₀ + δ).

Interpretación

Este resultado, aunque aparentemente simple, tiene un significado profundo. Muestra que la continuidad de una función impide que su signo cambie de manera súbita. Si en un punto la función es positiva, no puede volverse negativa de inmediato: antes debe pasar por el valor cero. De modo análogo, si en un punto es negativa, seguirá siéndolo en una vecindad cercana.

El teorema de la conservación del signo es una herramienta esencial en el análisis matemático. Sirve como base para resultados más avanzados, como el teorema de los valores intermedios y muchas propiedades de las funciones continuas.

Demostración alternativa

Supongamos que la función f(x) posee un límite finito $ l \ne 0 $ cuando $ x \to x_0 $.

$$ \lim_{x \to x_0} f(x) = l $$

Según la definición de límite finito, para todo $ \varepsilon > 0 $ existe un entorno de $ x_0 $ en el que se cumple

$$ | f(x) - l | < \varepsilon $$

Por la propiedad fundamental del valor absoluto, esta condición equivale a la doble desigualdad

$$ l - \varepsilon < f(x) < l + \varepsilon $$

Si elegimos $ \varepsilon = | l | $, obtenemos

$$ l - | l | < f(x) < l + | l | $$

A partir de aquí, analizamos dos situaciones posibles.

• Si el límite es positivo ( $ l > 0 $ ), entonces $$ 0 < f(x) < 2l $$  En consecuencia, la función resulta estrictamente positiva, $ f(x) > 0 $, en un entorno $ I $ de $ x_0 $.
• Si el límite es negativo ( $ l < 0 $ ), entonces $$ 2l < f(x) < 0 $$  En consecuencia, la función resulta estrictamente negativa, $ f(x) < 0 $, en un entorno $ I $ de $ x_0 $.

Esto demuestra que, si el límite es distinto de cero, la función conserva el signo de su límite en las proximidades del punto.

Teorema recíproco

Demostración

Procedamos por contradicción. Supongamos que f(x) es no negativa, $ f(x) \ge 0 $, en un entorno $ I(x_0) $, mientras que su límite es negativo ( $ l < 0 $ ).

Por el teorema de la permanencia del signo, si $ l < 0 $, existe un entorno $ I'(x_0) $ en el cual

$$ f(x) < 0 $$

Consideremos la intersección \( I(x_0) \cap I'(x_0) \), que sigue siendo un entorno de $ x_0 $. En dicho entorno deberían cumplirse simultáneamente

\[  f(x) \ge 0 \quad \text{y} \quad f(x) < 0 \]

lo cual es imposible.

La contradicción muestra que la hipótesis \( l < 0 \) no puede ser cierta. Por lo tanto, el límite debe satisfacer

\[ l \ge 0 \]

Con ello se concluye la demostración.

Nota La segunda afirmación se prueba del mismo modo. Basta suponer \( f(x) \le 0 \) en un entorno de \( x_0 \) y excluir por contradicción la posibilidad \( l > 0 \), apelando nuevamente al teorema de la permanencia del signo.