Teorema del límite de una función monótona

Cuando una función f(x) es monótona en el intervalo cerrado [a,b], es decir, mantiene una única dirección de crecimiento en todo ese tramo, podemos asegurar que posee límites finitos en cualquier punto \( x_0 \) del intervalo abierto (a,b). En particular: $$ \lim_{x \rightarrow x_0^-} = l \\ \lim_{x \rightarrow x_0^+} = l $$ Además, existe un límite finito por la derecha en el extremo izquierdo: $$ \lim_{x \rightarrow a^+} = l_a $$ y un límite finito por la izquierda en el extremo derecho: $$ \lim_{x \rightarrow b^-} = l_b $$

Un “límite finito” es simplemente un número real. No hablamos de infinito, sino de un valor bien definido.

¿Qué significa que una función sea monótona? Significa que no cambia de dirección. Si es creciente, siempre crece. Si es decreciente, siempre decrece. Esa regularidad es la clave que permite garantizar la existencia de límites finitos.

Ejemplo ilustrativo

Observemos la función \( f(x)=x^3 \) en el intervalo [-1,1]. Esta función es estrictamente creciente, por lo que constituye un ejemplo claro de función monótona.

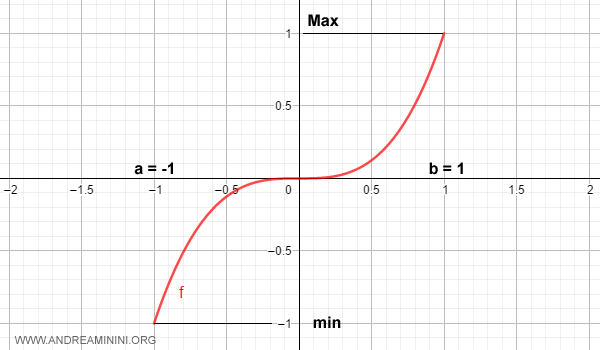
En cualquier punto \( x_0 \) del intervalo (-1,1), el límite de f(x) al acercarse a \( x_0 \) existe y coincide con el valor de la función en ese punto:

$$ \lim_{x \rightarrow x_0^-} x^3 = \lim_{x \rightarrow x_0^+} x^3 = f(x_0) $$

En los extremos ocurre lo mismo, tomando límites laterales:

$$ \lim_{x \rightarrow -1^+} x^3 = f(-1) \qquad \lim_{x \rightarrow 1^-} x^3 = f(1) $$

Cómo se demuestra

Supongamos que f(x) es creciente en el intervalo cerrado [a,b]. Esta propiedad garantiza que la función alcanza un mínimo en f(a) y un máximo en f(b). En otras palabras, f(x) permanece acotada en todo el intervalo.

Ejemplo. La función \( f(x) = \frac{x}{2} \) es estrictamente creciente en [2,6], con valores extremos f(2)=1 y f(6)=3.

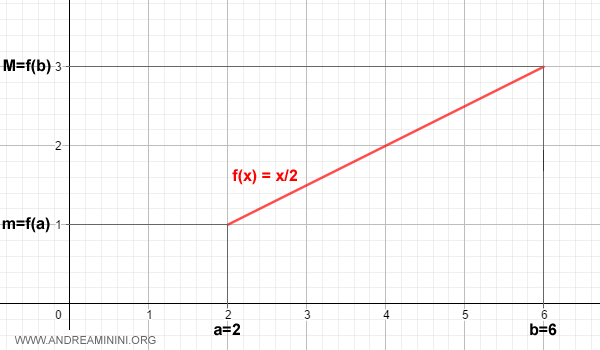
Si f(a) es su mínimo y f(b) su máximo, entonces para cualquier x en el intervalo:

$$ f(a) \le f(x) \le f(b) $$

Tomemos ahora un punto \( x_0 \in (a,b] \). Para estudiar el comportamiento de f(x) al acercarnos a \( x_0 \) desde la izquierda, analizamos el supremo de los valores de la función en el intervalo [a,\( x_0 \)):

$$ l' = \sup \{ f(x) : x \in [a, x_0) \} $$

Como f(x) es monótona y está acotada por arriba, este supremo es un número real. Además, para cualquier \( \epsilon > 0 \), existe un punto \( x_1 \in [a, x_0) \) tal que:

$$ l' - \epsilon < f(x_1) $$

Y por definición de supremo:

$$ l' - \epsilon < f(x_1) \le l' < l' + \epsilon $$

La monotonía implica que para todos los puntos posteriores a \( x_1 \), los valores de la función permanecen dentro de ese margen:

$$ l' - \epsilon < f(x_1) \le f(x) \le l' < l' + \epsilon $$

Esto demuestra que existe un límite al acercarse a \( x_0 \) por la izquierda:

$$ \lim_{x \rightarrow x_0^-} f(x) = l' $$

El razonamiento por la derecha es similar. Consideramos ahora el intervalo (\( x_0 \), b] y calculamos el ínfimo:

$$ l' = \inf \{ f(x) : x \in (x_0, b] \} $$

Este valor también es real, puesto que la función está acotada por abajo. Para cualquier \( \epsilon > 0 \), existe un punto \( x_1 \in (x_0, b] \) con:

$$ f(x_1) < l' + \epsilon $$

Y por definición de ínfimo:

$$ l' - \epsilon < l' \le f(x_1) < l' + \epsilon $$

La monotonía nos permite extender la desigualdad a cualquier x anterior a \( x_1 \):

$$ l' - \epsilon < l' \le f(x) \le f(x_1) < l' + \epsilon $$

Con esto queda establecido el límite por la derecha:

$$ \lim_{x \rightarrow x_0^+} f(x) = l' $$

Si ambos límites laterales existen y son finitos, entonces el límite total también existe:

$$ \lim_{x \rightarrow x_0} f(x) = l' $$

Esta idea se puede extender a cualquier punto del intervalo, lo que confirma la solidez del teorema.