Criterio de continuidad para funciones monótonas
Una función f(x) que es monótona en un intervalo cerrado y acotado [a,b] es una función continua si y solo si su imagen Im(f) contiene todos los valores comprendidos entre f(a) y f(b). En otras palabras, no deja huecos en ese rango. $$ Im(f) = \{ f(a), ... , f(b) \} $$
Un ejemplo práctico
Tomemos una función muy sencilla, estrictamente creciente en el intervalo [-1,1]:
$$ f(x) = x^3 \:\:\: \forall x \in [-1,1] $$
Su gráfica es la siguiente:
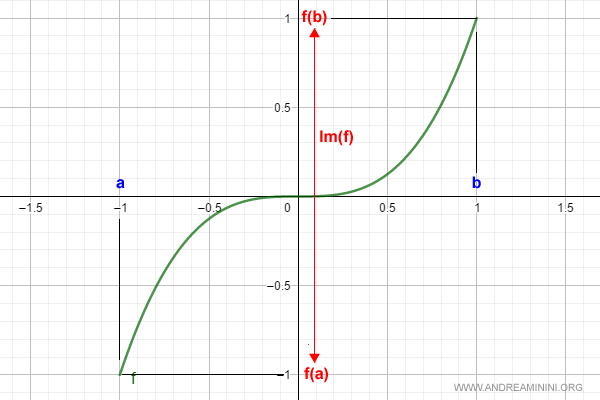
En este caso, la imagen de f(x) recorre sin interrupciones todos los valores entre f(a) y f(b), lo que confirma que la función es continua en ese intervalo.
Por qué ocurre esto
Decimos que una función es monótona cuando nunca cambia de sentido: a lo largo del intervalo [a,b] o bien siempre crece o bien siempre disminuye. Esta propiedad ordenada facilita mucho el análisis de su comportamiento.
Si la función es continua
Cuando f(x) es continua en todo el intervalo, sus valores están necesariamente comprendidos entre los valores que toma al inicio y al final.
- Si es creciente: $$ f(a) \le f(x) \le f(b) \:\:\: \forall x \in [a,b] $$
- Si es decreciente: $$ f(b) \le f(x) \le f(a) \:\:\: \forall x \in [a,b] $$
Además, el Teorema del Valor Intermedio garantiza que f(x) pasa por todos los valores intermedios. No se salta ninguno. Este es el fundamento del criterio de continuidad para funciones monótonas.
Si la función no es continua
Si aparece un punto \( x_0 \) en el que la función no es continua, el comportamiento cambia completamente. En ese punto surge una discontinuidad de primera especie: un salto entre los límites laterales.
$$ \lim_{x \rightarrow x_0^-} = l_1 < l_2 = \lim_{x \rightarrow x_0^+} $$
Entre \( l_1 \) y \( l_2 \) la función no toma valores. Se produce un hueco real en la imagen. Como resultado, f(x) deja de cubrir todos los valores entre f(a) y f(b), lo que contradice el criterio de continuidad.
Así queda clara la relación entre monotonicidad y continuidad.
Nota. Si la discontinuidad se presenta justo en un extremo del intervalo, es suficiente tomar \( x_0 = a \) o \( x_0 = b \). En cualquiera de los dos casos, sea la función creciente o decreciente, su imagen deja de cubrir por completo el rango entre f(a) y f(b).
Y así continúa el análisis.