Criterio para la invertibilidad de las funciones

Una función continua y estrictamente monótona en un intervalo [a,b] es una función invertible en ese mismo tramo. $$ y = f(x) \: \forall x \in [a,b] $$ $$ x = f^{-1}(y) \: \forall y \in [f(a),f(b)] $$

Esto significa que en el intervalo [a,b] existe una función inversa, que se representa como f^-1.

Un ejemplo práctico para entender la idea

Tomemos una función muy sencilla, continua y estrictamente monótona en [0,5]:

$$ f(x) = 2x $$

Su gráfico es el siguiente:

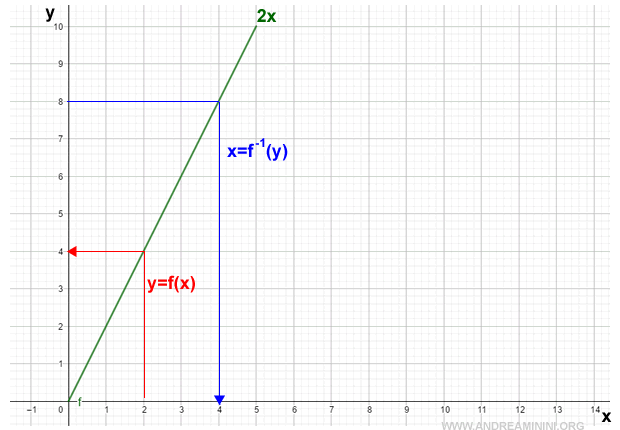
Esta función, al no cambiar de dirección y crecer de forma constante, es invertible en todo el intervalo.

$$ y = 2x $$

$$ x = \frac{y}{2} $$

Por lo tanto, su inversa es:

$$ f^{-1}(y) = \frac{y}{2} $$

Esto se traduce en una relación unívoca: cada valor \( y_0 \) dentro de la imagen de la función corresponde a un único \( x_0 \) en [0,5].

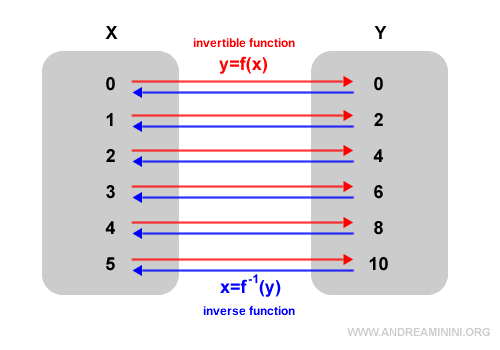
Cómo se demuestra

Consideremos una función estrictamente creciente en el intervalo [a,b]:

$$ f(a) < f(x) < f(b) \: \forall x \in (a,b) $$

Al crecer de manera estricta, f(a) actúa como valor mínimo y f(b) como máximo.

El Teorema del Valor Intermedio garantiza que una función continua en un intervalo cerrado [a,b] toma todos los valores comprendidos entre estos dos extremos.

$$ y \in [ f(a), f(b) ] $$

Así, para cada valor \( y \) del intervalo [f(a),f(b)], existe al menos un valor \( x \) tal que f(x)=y.

El paso clave es demostrar que ese valor de x es único.

Motivo. Una función invertible no puede asignar dos valores diferentes de x a un mismo valor de y. Debe existir siempre una correspondencia uno a uno entre ambos conjuntos.

Para probarlo, recurrimos a una contradicción. Supongamos que existen dos puntos distintos \( x_1 \) y \( x_2 \), con \( x_1 < x_2 \), tales que:

$$ f(x_1) = f(x_2) = y $$

Pero si la función es estrictamente creciente, necesariamente debería cumplirse:

$$ f(x_1) < f(x_2) $$

Por qué ocurre esto. Una función estrictamente creciente cumple que si un punto está a la izquierda de otro en el eje x, entonces su imagen está por debajo en el eje y. No puede mantenerse igual ni disminuir.

La condición anterior contradice la igualdad \( f(x_1) = f(x_2) \). Por lo tanto, solo es posible que la igualdad se cumpla cuando:

$$ x_1 = x_2 $$

Esto establece que cada valor de y se asocia a un único valor de x. La función tiene inversa en todo el intervalo.

$$ f:[a,b] \Leftrightarrow f:[f(a),f(b)] $$

En resumen, toda función continua y estrictamente monótona en un intervalo cerrado es necesariamente invertible en ese intervalo.

Y así continúa el razonamiento.