Infinidades de orden creciente
Cuando una sucesión diverge a infinito para n→∞, es posible comparar su velocidad de crecimiento mediante el criterio del cociente para sucesiones. Las sucesiones que crecen más rápido que otras se denominan infinidades de orden creciente.
Qué significa una infinidad de orden creciente
Una infinidad de orden creciente es una sucesión que no solo tiende a infinito, sino que lo hace a un ritmo significativamente mayor que otras sucesiones divergentes tomadas como referencia. Este tipo de comparación permite clasificar distintos comportamientos de crecimiento y entender qué sucesiones dominan sobre otras.
Un ejemplo para entender la idea
Consideremos dos sucesiones para k > 0:
$$ n^k $$
$$ k^n $$
Ambas son positivas y divergen cuando n→∞:
$$ \lim_{ n \rightarrow \infin;} n^k = \infin $$
$$ \lim_{ n \rightarrow \infin;} k^n = \infin $$
A simple vista, las dos crecen sin límite. Sin embargo, la pregunta relevante es cuál de ellas lo hace con mayor rapidez cuando n aumenta.
Para investigarlo, definimos la sucesión an como el cociente entre ambas:
$$ a_n = \frac{ n^k }{ k^n } $$
Luego analizamos su comportamiento comparando términos consecutivos mediante otra sucesión, bn:
$$ b_n = \frac{a_{n+1}}{a_n} $$
Desarrollando el cociente:
$$ b_n = \frac{ \frac{ (n+1)^k }{ k^{(n+1)} } }{ \frac{ n^k }{ k^n } } $$
$$ b_n = \frac{ (n+1)^k }{ k^{n+1} } \cdot \frac{ k^n }{ n^k } $$
$$ b_n = \frac{ (n+1)^k }{ k \cdot n^k } $$
$$ b_n = \frac{1}{k} \cdot \frac{ (n+1)^k }{ n^k } $$
$$ b_n = \frac{1}{k} \cdot \left( \frac{ n+1 }{ n } \right)^k $$
Ahora calculamos el límite cuando n→∞:
$$ \lim_{ n \rightarrow \infin;} b_n $$
$$ \lim_{ n \rightarrow \infin;} \frac{1}{k} \cdot \left( \frac{ n+1 }{ n } \right)^k $$
Como (n+1)/n tiende a 1, obtenemos:
$$ \lim_{ n \rightarrow \infin;} \frac{1}{k} \cdot \left( \frac{ n+1 }{ n } \right)^k = \frac{1}{k} < 1 $$
Este resultado, junto con el criterio del cociente para sucesiones, nos indica que:
$$ \lim_{ n \rightarrow \infin;} a_n = \lim_{ n \rightarrow \infin;} \frac{ n^k }{ k^n } = 0 $$
Por tanto, la sucesión kn crece mucho más rápido que nk. En otras palabras, kn es una infinidad de orden superior.
La gráfica siguiente muestra con claridad esta diferencia de crecimiento:
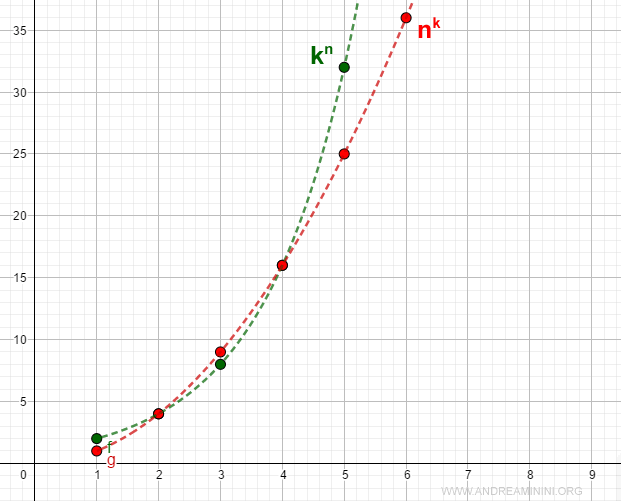
A medida que n aumenta, la distancia entre ambas sucesiones se hace cada vez mayor. Mientras nk crece de forma relativamente moderada, kn lo hace de manera explosiva, dominando por completo la comparación.
Este tipo de análisis es clave para estudiar el comportamiento asintótico de sucesiones y funciones, y constituye una herramienta fundamental en cálculo, teoría de números y análisis asintótico.