Teorema de continuidad de la función inversa
Cuando una función f(x) es estrictamente monótona en un intervalo cerrado [a,b], su continuidad está completamente ligada a la de su función inversa f-1(x). En términos simples, una es continua si, y solo si, la otra también lo es.
Un ejemplo para entenderlo
Observemos la función siguiente, que es estrictamente creciente en el intervalo [-2,2]:
$$ y = f(x) = 2x $$
Esta función es invertible y su inversa se obtiene de inmediato:
$$ x = f^{-1}(y) = \frac{y}{2} $$
Así se ve su gráfica en el plano cartesiano:
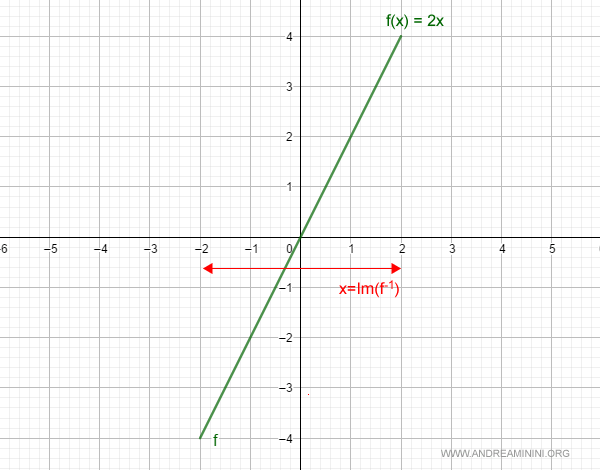
Para analizar la continuidad de f(x), aplicamos el criterio de continuidad para funciones monótonas directamente a su inversa.
Nota. El criterio de continuidad para funciones monótonas afirma que una función es continua si su imagen Im(f) cubre sin interrupciones todos los valores entre f(a) y f(b).
En nuestro ejemplo trabajamos con:
$$ f^{-1}(y) = \frac{y}{2} $$
Su dominio es:
$$ y \in [-4,4] $$
Evaluando en los extremos obtenemos:
$$ f^{-1}(-4) = -2 \\ f^{-1}(4) = 2 $$
La imagen de la función inversa es, por tanto:
$$ Im(f^{-1}) = [-2,2] $$
Es decir, la inversa recorre de forma continua todos los valores dentro de ese intervalo. Por ello, y gracias al teorema, confirmamos que f(x) = 2x es una función continua.
Cómo se fundamenta el teorema
Una función estrictamente monótona definida en un intervalo cerrado siempre admite una inversa. Esa inversa se obtiene invirtiendo la relación entre x y y:
$$ y = f(x) $$
$$ x = f^{-1}(y) $$
Nota. Una función es estrictamente monótona cuando no deja de crecer o de decrecer en ningún momento dentro del intervalo. No mantiene tramos constantes.
Según el comportamiento de la función, pueden darse dos situaciones:
- Si f(x) es estrictamente creciente: $$ f:[a,b] \rightarrow [f(a), f(b)] $$ $$ f^{-1}:[f(a), f(b)] \rightarrow [a,b] $$
- Si f(x) es estrictamente decreciente: $$ f:[a,b] \rightarrow [f(b), f(a)] $$ $$ f^{-1}:[f(b), f(a)] \rightarrow [a,b] $$
En cualquiera de los dos casos, la imagen de la función inicial cubre exactamente todos los valores comprendidos entre sus extremos. Ese es el punto clave.
Como la inversa reproduce de forma continua todos los valores del intervalo correspondiente, deducimos que la función original también es continua.
Nota. El criterio de continuidad para funciones monótonas nos recuerda que no basta con que la función sea monotónica. Para ser continua, su imagen debe cubrir todo el intervalo entre los valores extremos sin saltos.
Si su función inversa cumple esta condición, la función original la cumple también. Así queda completada la demostración de este resultado fundamental para el análisis de funciones.