Funciones Acotadas y No Acotadas

¿Qué es una función acotada?

Una función acotada es aquella cuyos valores $f(x)$ permanecen siempre dentro de un intervalo limitado por un mínimo y un máximo.

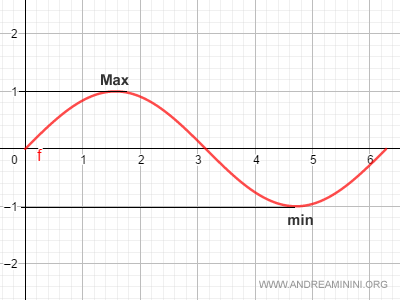
Geométricamente, la gráfica de una función acotada queda contenida por completo entre dos rectas horizontales (paralelas al eje x).

En este tipo de funciones, el conjunto de valores está comprendido entre dos números reales:

• Mínimo: el valor más pequeño que alcanza $f(x)$ en un intervalo $[a, b]$
• Máximo: el valor más grande que alcanza $f(x)$ en un intervalo $[a, b]$

Si no es posible encontrar dos números reales que limiten la imagen de la función, se dice que la función es no acotada.

Ejemplo de función no acotada: La función $f(x) = x^3$ es no acotada, pues no posee un mínimo ni un máximo finito.

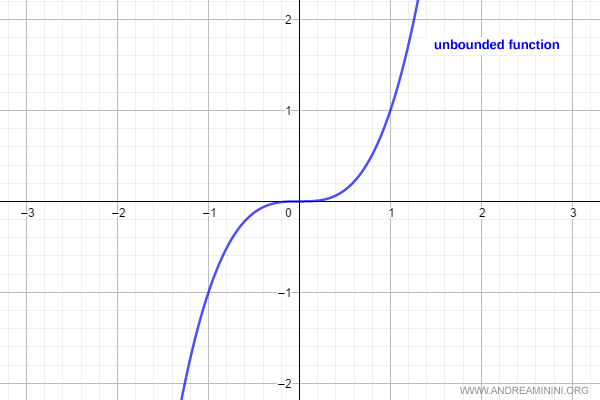
Una función se considera acotada cuando está limitada tanto por arriba como por abajo.

Un Ejemplo Práctico

Consideremos la función seno:

$$ f(x) = \sin(x) $$

El dominio de esta función es el conjunto de todos los números reales:

$$ \text{Dom}(f) = \mathbb{R} $$

Su imagen está formada por infinitos valores comprendidos en el intervalo cerrado $[-1, 1]$:

$$ \text{Im}(f) = [-1, 1] $$

La imagen, por lo tanto, está acotada superior e inferiormente.

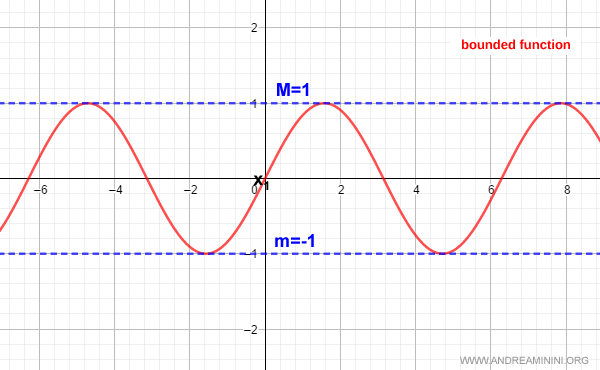
La función $f(x)$ alcanza tanto un valor máximo como un mínimo:

$$ M = 1 $$

$$ m = -1 $$

En consecuencia, la función seno está acotada en todo su dominio.

Funciones Acotadas Superiormente

Una función $f(x)$ definida en un intervalo $(a, b)$ está acotada superiormente si se cumple al menos una de las siguientes condiciones:

1. Existe un número real $M$ tal que $f(x) \le M$ para todo $x \in (a, b)$.
2. La imagen de $f(x)$ está limitada por arriba.
3. El supremo de la imagen es finito: $$ \sup(\text{Im}(f)) < +\infty $$

Si ninguna de estas condiciones se cumple, la función se considera no acotada superiormente.

Ejemplo: Una función acotada superiormente - $f(x)$ posee un valor máximo finito $M$.

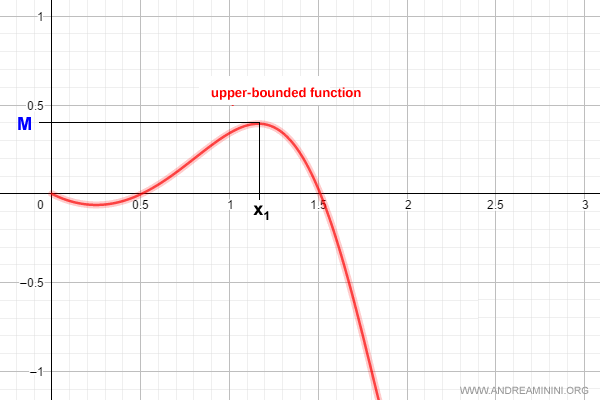
Funciones No Acotadas Superiormente

Una función $f(x)$ definida en $(a, b)$ es no acotada superiormente en su dominio si se cumple al menos una de las siguientes condiciones:

1. Para todo $M > 0$, existe algún $x \in (a, b)$ tal que $f(x) > M$.
2. La imagen de $f(x)$ no tiene límite superior.
3. El supremo de la imagen es infinito: $$ \sup(\text{Im}(f)) = +\infty $$

Ejemplo: Una función no acotada superiormente.

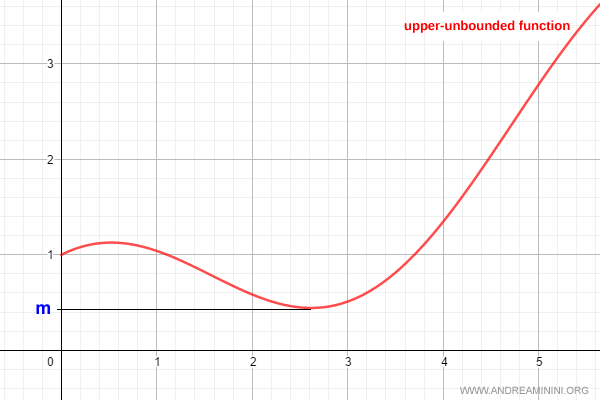
Funciones Acotadas Inferiormente

Una función $f(x)$ definida en un intervalo $(a, b)$ está acotada inferiormente si se cumple al menos una de las siguientes condiciones:

1. Existe un número real $m$ tal que $f(x) \ge m$ para todo $x \in (a, b)$.
2. La imagen de $f(x)$ está limitada por abajo.
3. El ínfimo de la imagen es finito: $$ \inf(\text{Im}(f)) > -\infty $$

Si ninguna de estas condiciones se cumple, se dice que la función es no acotada inferiormente.

Ejemplo: Una función acotada inferiormente - $f(x)$ alcanza un valor mínimo $m$.

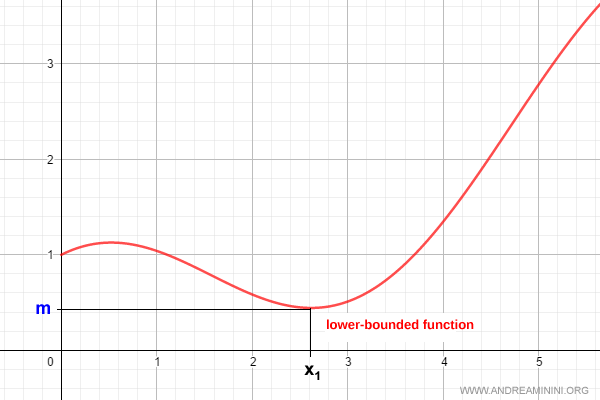
Funciones No Acotadas Inferiormente

Una función $f(x)$ definida en $(a, b)$ es no acotada inferiormente en su dominio si se cumple al menos una de las siguientes condiciones:

1. Para todo $m \in \mathbb{R}$, existe algún $x \in (a, b)$ tal que $f(x) < m$.
2. La imagen de $f(x)$ no tiene límite inferior.
3. El ínfimo de la imagen es infinito: $$ \inf(\text{Im}(f)) = -\infty $$

Ejemplo: Una función no acotada inferiormente.

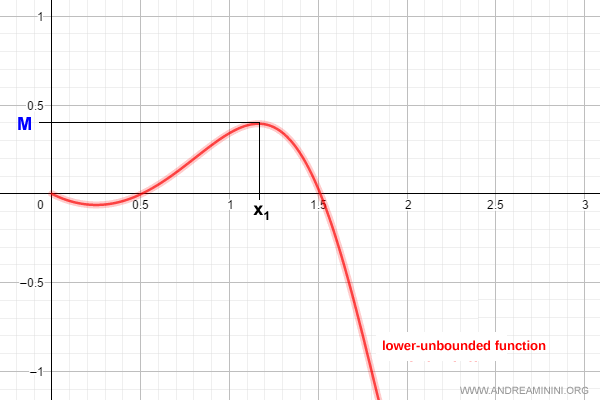
Y así sucesivamente.