Función cuadrática
Una función cuadrática es toda función que puede expresarse en la forma $$ y = ax^2 + bx + c $$ donde el coeficiente principal \( a \neq 0 \).
La gráfica de una función cuadrática es una parábola.
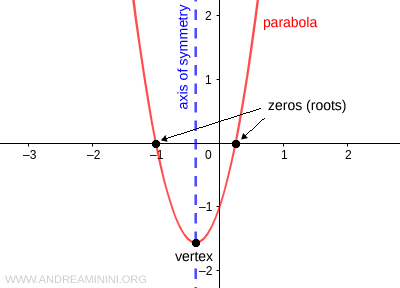
El eje de simetría de la parábola es una recta vertical:
$$ x = - \frac{b}{2a} $$
El vértice de la parábola corresponde al punto V:
$$ V \begin{pmatrix} \ - \frac{b}{2a} \ ; \ - \frac{b^2-4ac}{4a} \ \end{pmatrix} $$
Las raíces (o ceros) de una función cuadrática son los valores de \( x \) en los que la parábola corta el eje de abscisas. Se llaman “ceros” porque en esos puntos la función toma el valor \( y=0 \).
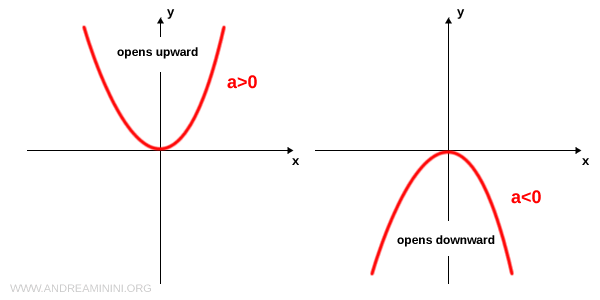
La concavidad de la parábola depende exclusivamente del signo del coeficiente principal \( a \):
- a>0
Si \( a>0 \), la parábola se abre hacia arriba. - a<0
Si \( a<0 \), la parábola se abre hacia abajo.
La anchura de la parábola está determinada por el valor absoluto de \( a \).
Cuanto mayor sea el valor absoluto |a|, más estrecha será la parábola; cuanto menor sea |a|, más abierta resultará.
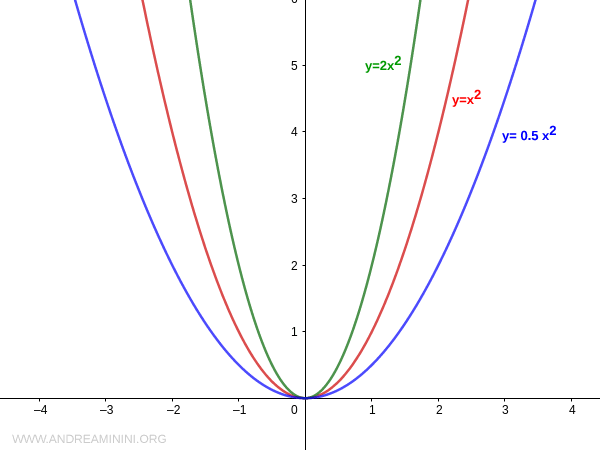
Nota. La “apertura” de la parábola se refiere a la separación entre su curva y el eje de simetría. Un valor absoluto de |a| más pequeño hace que la parábola se ensanche, acercándose gradualmente a dicho eje.
Ejemplo resuelto
Consideremos la siguiente función cuadrática:
$$ y = 4x^2 + 3x - 1 $$
Como el coeficiente principal es \( a = 4 \), positivo, la parábola se abre hacia arriba.
Para calcular las raíces (los puntos de corte con el eje x), resolvemos la ecuación cuadrática asociada:
$$ 4x^2 + 3x - 1 = 0 $$
El discriminante resulta ser positivo:
$$ \Delta = b^2 - 4ac = 3^2 - 4(4)(-1) = 9 + 16 = 25 $$
Por tanto, la ecuación posee dos soluciones reales distintas:
$$ x = \frac{-b \pm \sqrt{\Delta} }{2a} = \frac{-3 \pm \sqrt{25}}{2(4)} = \frac{-3 \pm 5}{8} = \begin{cases} x_1 = \frac{-3 - 5}{8} = -1 \\ \\ x_2 = \frac{-3 + 5}{8} = \tfrac{1}{4} \end{cases} $$
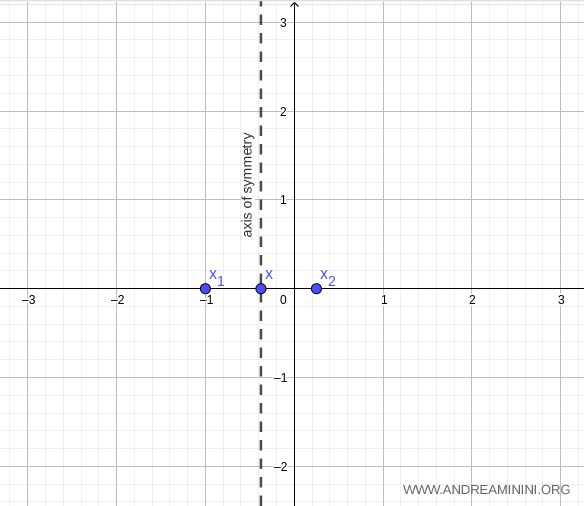
Así, las raíces de la función cuadrática son \( x_1 = -1 \) y \( x_2 = \tfrac{1}{4} \).
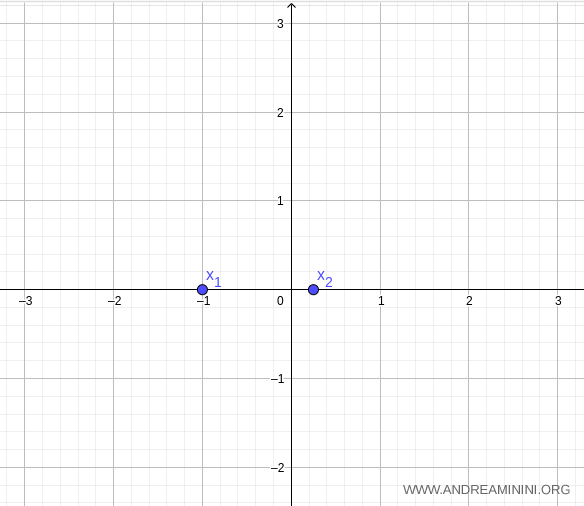
Calculemos ahora el eje de simetría, con \( a=4, b=3, c=-1 \):
$$ x = - \frac{b}{2a} = - \frac{3}{2 \cdot 4} = - \frac{3}{8} $$
El eje de simetría es la recta vertical perpendicular al eje x en \( x = -\tfrac{3}{8} \).
A continuación hallamos el vértice de la parábola:
$$ V \begin{pmatrix} \ - \frac{b}{2a} \ ; \ - \frac{b^2-4ac}{4a} \ \end{pmatrix} = \begin{pmatrix} - \tfrac{3}{8} ; - \tfrac{25}{16} \end{pmatrix} $$
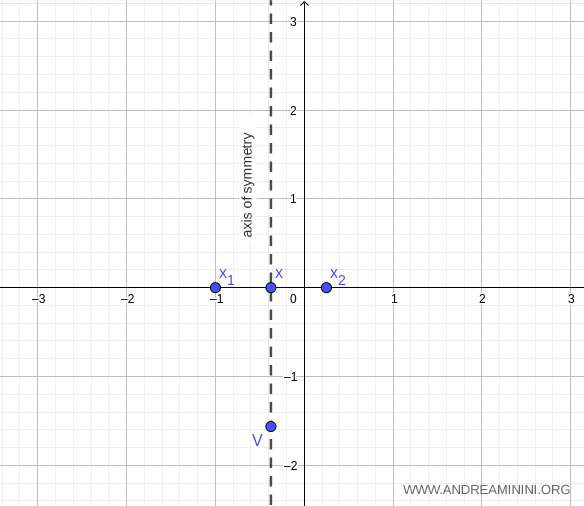
El vértice de la parábola es el punto \( V \left(-\tfrac{3}{8}, -\tfrac{25}{16}\right) \).
Para representar la curva con mayor precisión, podemos calcular valores adicionales de \( y \) en torno al eje de simetría:
Dada la función y = 4x2 + 3x - 1:
$$ \begin{array}{c|lcr} x & y \\ \hline -2 & 9 \\ -1 & 0 \\ 0 & -1 \\ 1 & 6 \end{array} $$
Con estos valores es posible trazar la gráfica de la parábola:
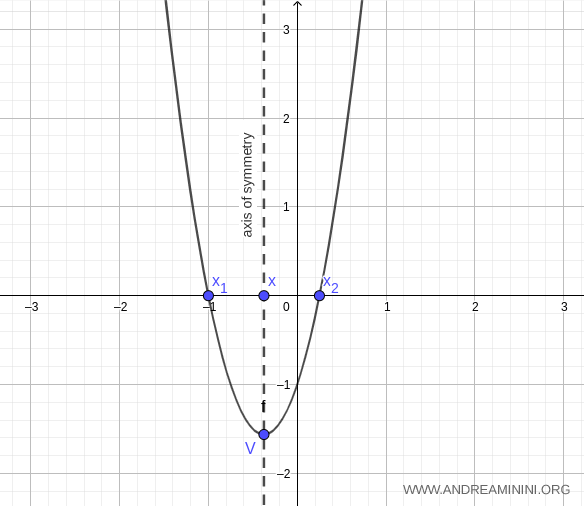
El procedimiento puede prolongarse siguiendo el mismo método.