Parábolas

Una parábola es una curva algebraica plana de segundo grado, definida como el conjunto de todos los puntos que se encuentran a la misma distancia de un punto fijo llamado foco (F) y de una recta fija denominada directriz, la cual no pasa por el foco.

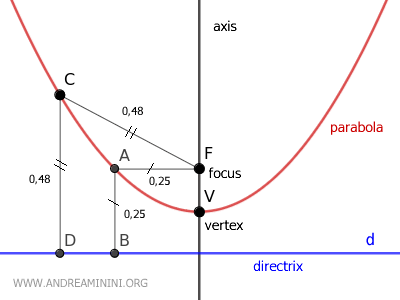
Dicho de otro modo, los puntos que forman la parábola constituyen un lugar geométrico, ya que están equidistantes del foco (F) y de la directriz (d).

El eje de la parábola es la recta que pasa por el foco y es perpendicular a la directriz.

El vértice es el punto de intersección entre la parábola y su eje.

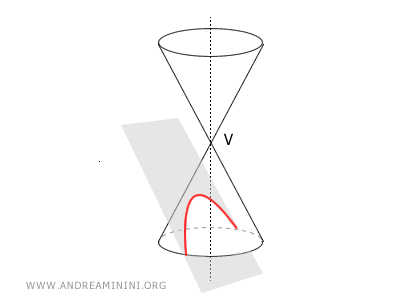
Otra forma de definir una parábola es como la sección cónica resultante de cortar un cono circular infinito con un plano paralelo a su generatriz.

 

Nota: La parábola tiene numerosas aplicaciones en física, ingeniería y otras disciplinas científicas. Por ejemplo, en física puede describir la trayectoria de un proyectil en ausencia de resistencia del aire.

La ecuación de una parábola

La forma canónica de la ecuación de una parábola cuyo eje de simetría es paralelo al eje y es:

$$ y = ax^2 + bx + c $$

donde a, b y c son coeficientes reales, con a distinto de cero (a ≠ 0).

Nota: La amplitud de la parábola depende del valor absoluto del coeficiente "a". A mayor |a|, más estrecha será la parábola; a menor |a|, más ancha. El signo de "a" también determina el sentido de apertura: si a > 0, se abre hacia arriba (cóncava hacia arriba); si a < 0, se abre hacia abajo (cóncava hacia abajo).

Si el eje de simetría es horizontal, la forma estándar de la ecuación es:

$$ x = ay^2 + by + c $$

Los elementos principales de una parábola son los siguientes:

• Foco
  El foco (F) es un punto fijo situado en el interior de la parábola. Sus coordenadas se determinan mediante la fórmula: $$ F \begin{pmatrix} - \frac{b}{2a} \ , \ \frac{1-Δ}{4a} \end{pmatrix} $$ donde a, b y c son los coeficientes de la parábola y = ax² + bx + c, y Δ representa el discriminante: Δ = b² - 4ac.
• Directriz
  La directriz (d) es una recta fija situada fuera de la parábola. Su ecuación es: $$ y = - \frac{1 + Δ}{4a} $$
• Eje
  El eje es una recta perpendicular a la directriz (d) que pasa por el foco (F). Además de ser el eje geométrico de la parábola, actúa como eje de simetría, dividiéndola en dos mitades especulares. Su ecuación es: $$ x = - \frac{b}{2a} $$
• Vértice
  El vértice (V) es el punto donde la parábola corta a su eje. Allí alcanza su valor máximo o mínimo, dependiendo del signo del coeficiente "a" en la ecuación y = ax² + bx + c. Las coordenadas del vértice se obtienen así: $$ V \begin{pmatrix} - \frac{b}{2a} \ , \ - \frac{Δ}{4a} \end{pmatrix} $$

Un ejemplo práctico

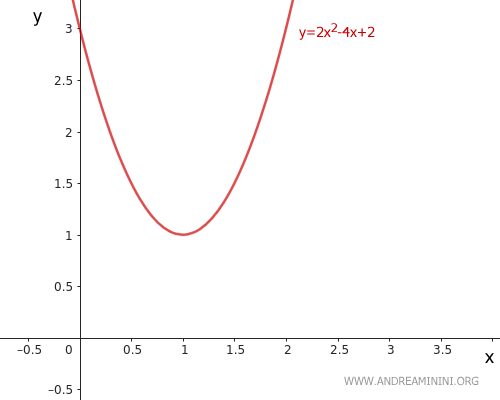
Consideremos la parábola dada por la siguiente ecuación:

$$ y = 2x^2 - 4x + 3 $$

Los coeficientes son a = 2, b = -4 y c = 3.

Como el coeficiente a es positivo, sabemos de inmediato que la parábola se abre hacia arriba.

Utilizamos la fórmula para calcular la ecuación de la directriz:

$$ y = - \frac{1 + Δ}{4a} $$

Con a = 2, b = -4 y c = 3, el discriminante es:

$$ Δ = (-4)^2 - 4 \cdot 2 \cdot 3 = 16 - 24 = -8 $$

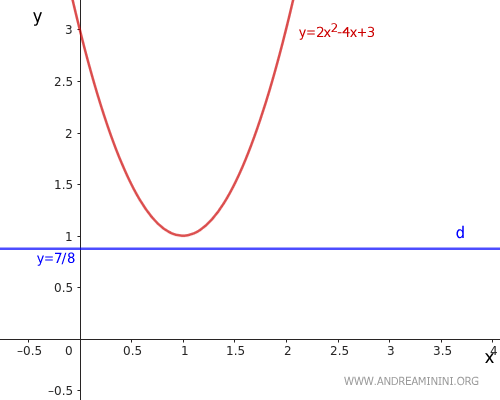
Por tanto, la ecuación de la directriz queda:

$$ y = - \frac{1 + Δ}{4a} = - \frac{1 - 8}{4 \cdot 2} = - \frac{-7}{8} = \frac{7}{8} $$

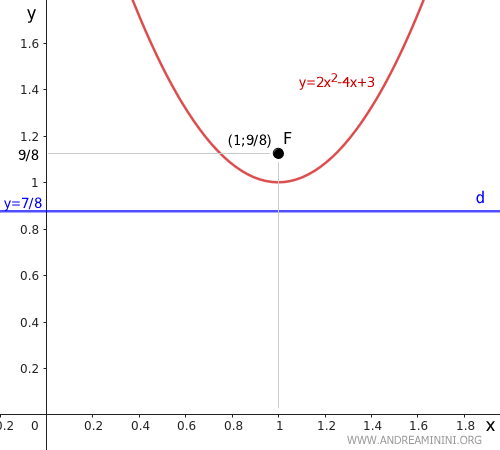
Agregamos la directriz (d) y = 7/8 al gráfico:

Ahora determinamos el foco (F) de la parábola:

$$ F \begin{pmatrix} - \frac{b}{2a} \ , \ \frac{1 - Δ}{4a} \end{pmatrix} $$

Sustituyendo los valores: a = 2, b = -4, c = 3 y Δ = -8:

$$ F \begin{pmatrix} - \frac{-4}{2 \cdot 2} \ , \ \frac{1 - (-8)}{4 \cdot 2} \end{pmatrix} $$

$$ F \begin{pmatrix} 1 \ , \ \frac{9}{8} \end{pmatrix} $$

Por tanto, el foco F se encuentra en las coordenadas (x, y) = (1, 9/8).

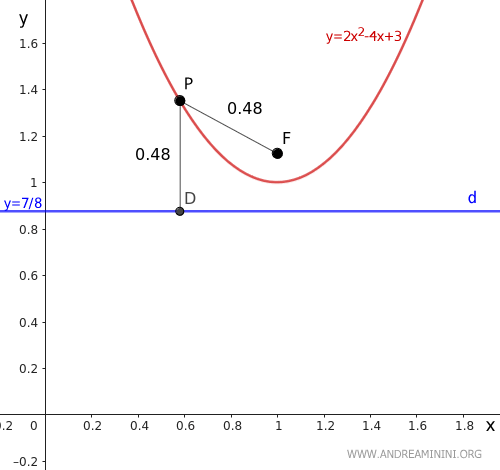
Como verificación, podemos tomar cualquier punto P sobre la parábola y comprobar que su distancia al foco F es igual a su distancia a la directriz d.

Estas distancias son iguales, PF ≈ PD, lo que confirma que los cálculos son correctos.

A continuación, calculamos la ecuación del eje de la parábola:

$$ x = - \frac{b}{2a} $$

Con a = 2 y b = -4, el resultado es:

$$ x = \frac{4}{4} = 1 $$

Así, el eje de la parábola es una recta vertical, paralela al eje y, que pasa por x = 1.

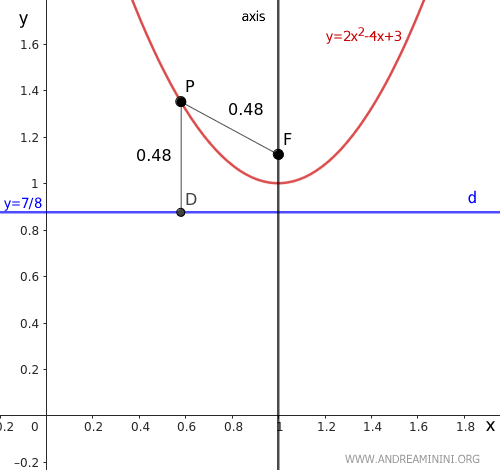
Por definición, el eje es perpendicular a la directriz (d) y pasa por el vértice (V) de la parábola.

En una parábola, el eje también es su eje de simetría.

Esto significa que para cada punto P en la parábola existe un punto simétrico P' a igual distancia del foco (F) y de la directriz (d).

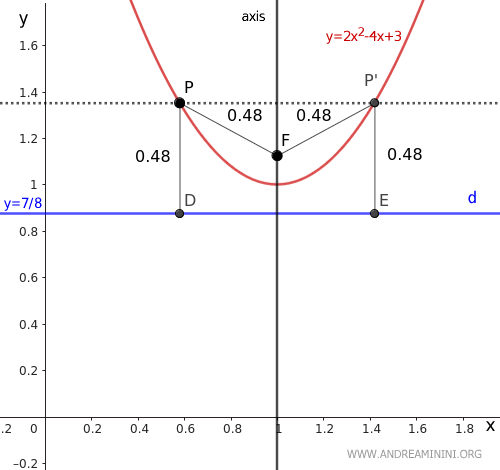
Finalmente, calculamos las coordenadas del vértice (V) y comprobamos que se encuentra sobre el eje:

$$ V \begin{pmatrix} - \frac{b}{2a} \ , \ - \frac{Δ}{4a} \end{pmatrix} $$

Con a = 2, b = -4, c = 3 y Δ = -8:

$$ V \begin{pmatrix} 1 \ , 1 \end{pmatrix} $$

El vértice V está en las coordenadas (x, y) = (1, 1).

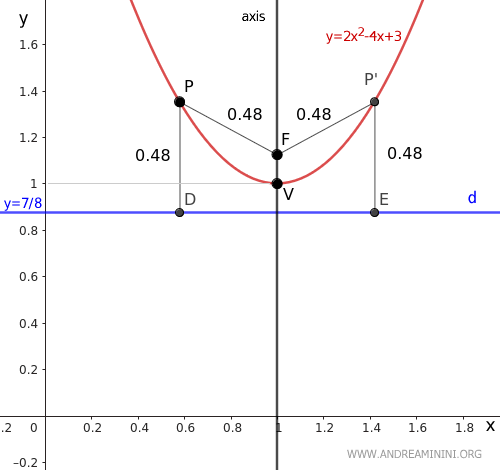
El vértice de la parábola se encuentra exactamente sobre el eje, lo que confirma la validez del resultado.

La gráfica de una parábola

La gráfica de una parábola representa una función cuadrática de la forma $$ y = ax^2 + bx + c $$, con a ≠ 0. Se trata de una curva plana abierta de segundo grado, simétrica respecto a su eje.

La ecuación general de la parábola es:

$$ y = ax^2 + bx + c $$

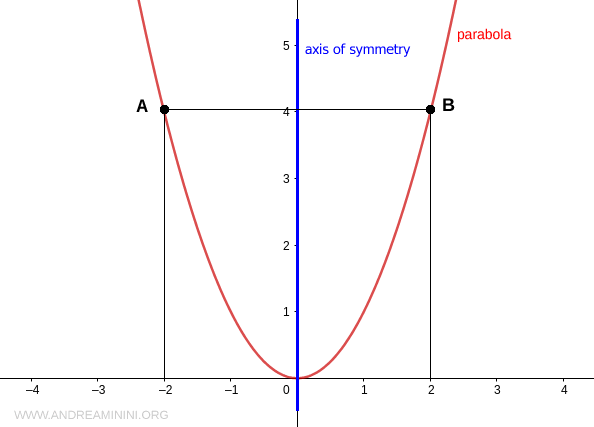
Desde el punto de vista geométrico, toda parábola se caracteriza por tener un eje de simetría.

Para cualquier par de puntos A y B que compartan la misma ordenada, dichos puntos son simétricos y equidistantes respecto al eje de simetría.

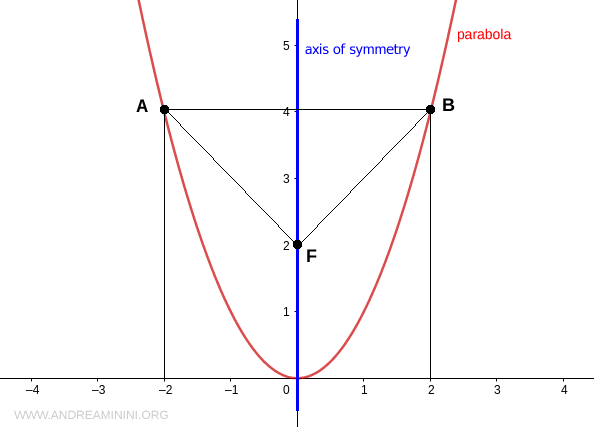
También están a la misma distancia de cualquier punto fijo sobre dicho eje, denominado foco (F).

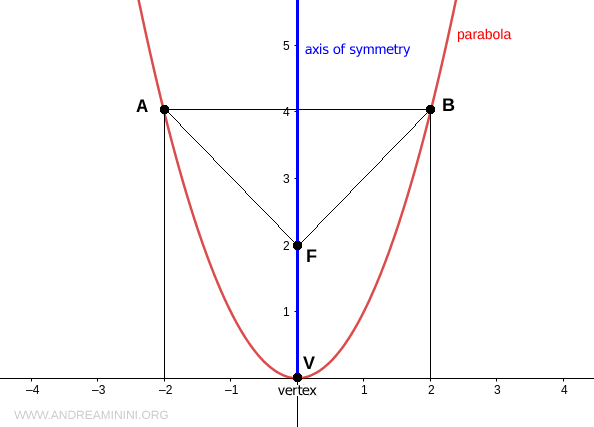
El punto donde la parábola corta su eje de simetría se llama vértice (V).

Si la ecuación es y = ax², el vértice de la parábola coincide con el origen O(0,0) del plano cartesiano.

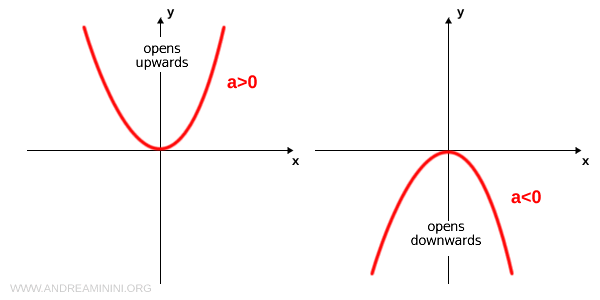
El signo del coeficiente a determina el sentido de la concavidad de la parábola.

• a > 0
  Si a > 0, la parábola se abre hacia arriba.
• a < 0
  Si a < 0, la parábola se abre hacia abajo.

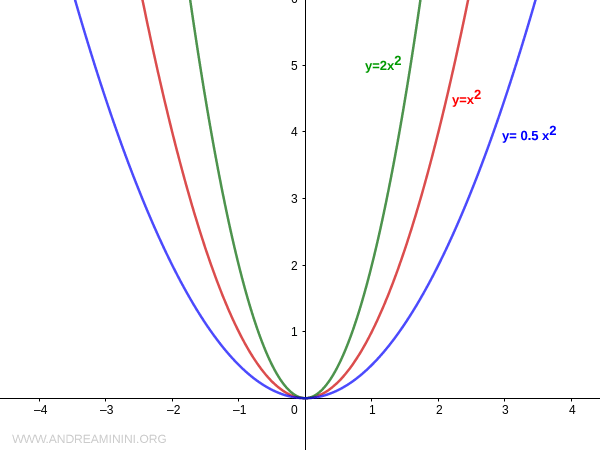
El valor absoluto del coeficiente |a| determina la apertura o estrechez de la parábola.

A mayor |a|, más cerrada será la parábola; a menor |a|, más abierta.

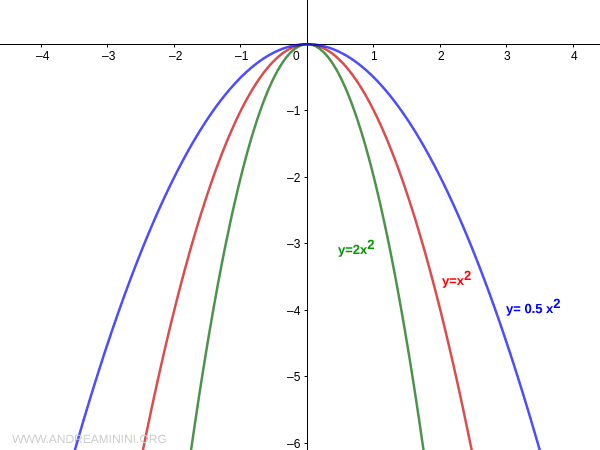
Esta relación también se mantiene si el coeficiente a es negativo:

Nota: El coeficiente a no puede ser igual a cero, ya que en ese caso la función dejaría de ser cuadrática y se convertiría en una función lineal o constante.

Observaciones

Algunas consideraciones y aspectos destacados sobre las parábolas:

• La parábola como sección cónica
  La parábola es una de las secciones cónicas, junto con la elipse, la hipérbola y la circunferencia. Se obtiene al cortar un cono circular con un plano paralelo a una de sus generatrices, intersectando únicamente una de sus napas. El resultado es una curva abierta y sin límites.
  

  

• El eje de la parábola es su eje de simetría
  Esto significa que para cada punto de la parábola existe otro simétrico respecto a dicho eje, lo que proporciona a la curva su característica forma equilibrada.
• Relación entre la apertura de la parábola y el valor absoluto de "a"
  La amplitud de la parábola depende directamente del valor absoluto del coeficiente "a". Si |a| es grande, la parábola es más estrecha; si |a| es pequeño, es más ancha.
  

  

• Concavidad y signo de "a"
  El signo de "a" en la ecuación y = ax² + bx + c determina la dirección de la concavidad: si a > 0, la parábola es cóncava hacia arriba; si a < 0, es cóncava hacia abajo.
  

  

  Nota: Se dice que una curva es cóncava si el segmento que une dos de sus puntos queda por debajo de la curva.

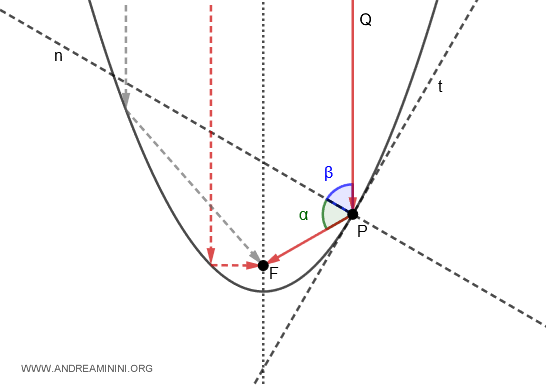
• Propiedad óptica de la parábola
  Si se traza la tangente (t) en un punto P de la parábola, la perpendicular (n) a dicha tangente divide en dos ángulos iguales el ángulo formado entre el rayo focal $ PF $ y el rayo $ PQ $ (paralelo al eje focal): $ \alpha \cong \beta $.
  
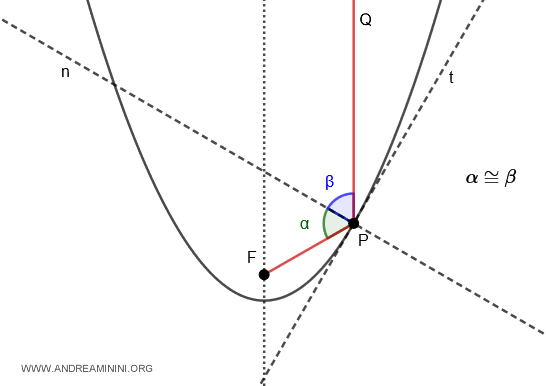
  Esta propiedad implica que cualquier rayo que incida paralelo al eje focal será reflejado hacia el foco (F). Por esta razón, todos los rayos paralelos convergen en un mismo punto. Este principio se aplica en antenas parabólicas y concentradores solares.
  
  De forma inversa, si el foco (F) actúa como fuente de luz, los rayos reflejados se propagan de manera paralela al eje focal.
  

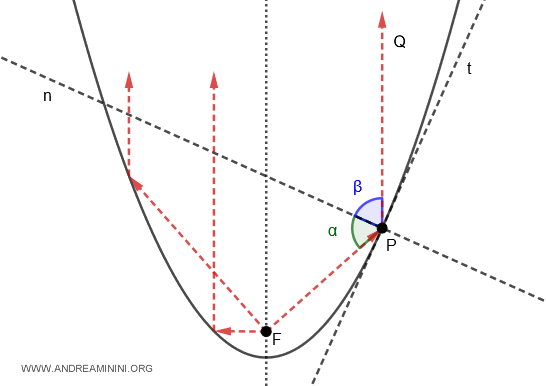
Y así sucesivamente.