Cómo determinar la ecuación de una parábola conociendo un punto y el foco

Para hallar la ecuación de una parábola a partir de un punto \((x_0, y_0)\) que pertenece a ella y de su foco \((x_F, y_F)\), es necesario disponer de información adicional que permita establecer la orientación de la parábola (por ejemplo, si es vertical u horizontal, si abre hacia arriba o abajo, hacia la derecha o la izquierda, etc.). Esta información suele proporcionarse en el enunciado del problema.

En caso contrario, se pueden considerar varias hipótesis simultáneamente.

• Parábola con eje vertical
  El eje de simetría es vertical y la directriz es horizontal. La parábola puede abrir hacia arriba o hacia abajo.
• Parábola con eje horizontal
  El eje de simetría es horizontal y la directriz es vertical. La parábola puede abrir hacia la derecha o hacia la izquierda.

Ejemplo práctico

Supongamos que se nos dan el punto \((1, 2)\) y el foco \((4, 6)\).

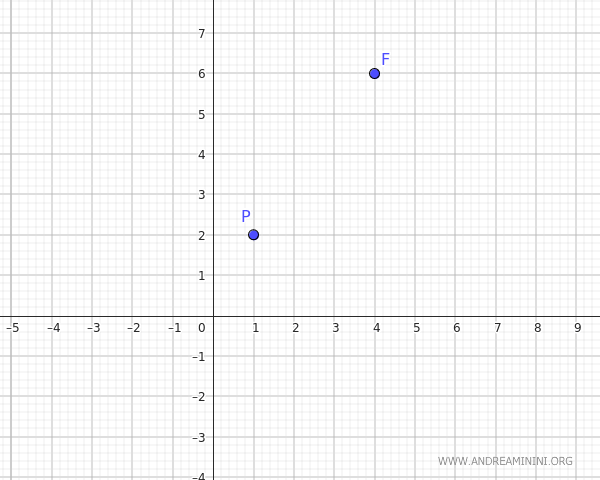
Queremos determinar si la parábola tiene eje de simetría vertical u horizontal.

Conociendo únicamente un punto y el foco no es posible establecer la orientación de la parábola. Por tanto, si el problema no proporciona más datos, debemos considerar ambas posibilidades.

1] Parábola con eje de simetría vertical

Conocemos las coordenadas de un punto \(P((x_0,y_0)=(1, 2))\) que pertenece a la parábola, y del foco \(F(x_F,y_F)=(4, 6)\). Si suponemos que el eje de simetría es vertical:

El foco y el vértice se encuentran sobre ese eje, por lo que comparten la misma coordenada \(x\): es decir, el vértice tiene coordenadas \( (h, k) = (4, k) \), por tanto \( h = 4 \).

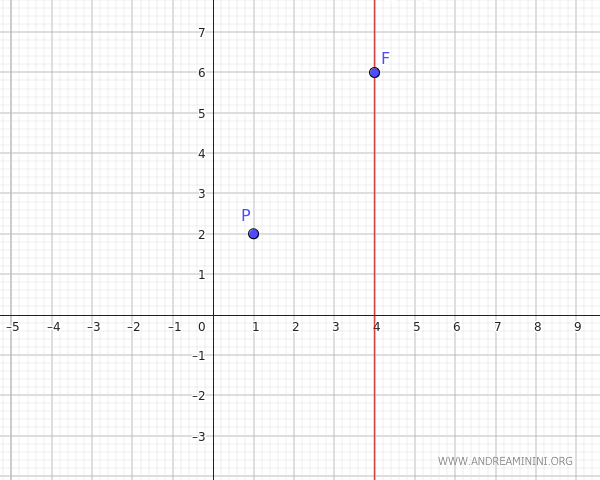
La ecuación general de una parábola con eje vertical es:

$$ (x - h)^2 = 4p(y - k) $$

donde \((h, k)\) es el vértice y \(p\) representa la distancia entre el vértice y el foco.

En este caso, como \(h = 4\), tenemos:

$$ (x - 4)^2 = 4p(y - k) $$

Por definición, la distancia entre cualquier punto \(P\) de la parábola y el foco es igual a la distancia entre ese mismo punto y la directriz.

Calculamos la distancia entre el punto \( P(1,2) \) y el foco \(F(4, 6)\):

$$ d_1 = \sqrt{(x_0 - x_F)^2 + (y_0 - y_F)^2} = \sqrt{(-3)^2 + (-4)^2} = \sqrt{9 + 16} = \sqrt{25} = 5 $$

La distancia entre \(P\) y el foco es igual a 5.

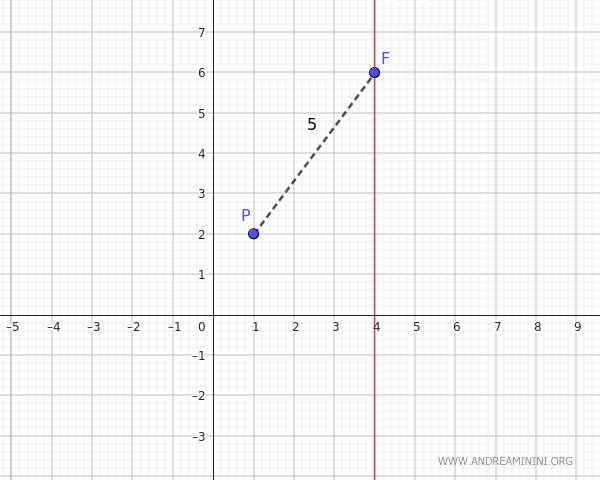
Como el eje de simetría es vertical y pasa por el foco \( (4,6) \), su ecuación es simplemente:

$$ x = 4 $$

La recta paralela al eje que pasa por el punto \( P(1,2) \) tiene la misma coordenada \(x\) que el punto, es decir, \( x = 1 \).

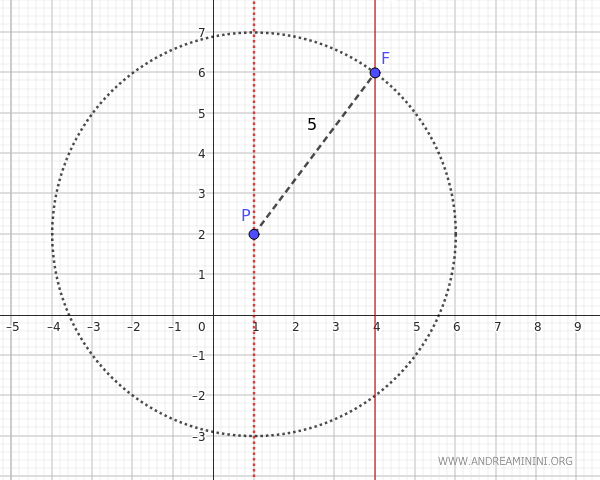
Para encontrar la directriz, hallamos los puntos de intersección entre la recta \( x = 1 \) y la circunferencia centrada en \(P(1,2)\) de radio \(d_1 = 5\):

$$ \begin{cases} x = 1 \\ \\ (x - 1)^2 + (y - 2)^2 = 25 \end{cases} $$

$$ (y - 2)^2 = 25 \Rightarrow y^2 - 4y + 4 = 25 \Rightarrow y^2 - 4y - 21 = 0 $$

Resolviendo la ecuación cuadrática:

$$ y = \frac{4 \pm \sqrt{100}}{2} = \frac{4 \pm 10}{2} \Rightarrow \begin{cases} y = 7 \\ \\ y = -3 \end{cases} $$

Por lo tanto, las posibles posiciones de la directriz son:

$$ y_D = 7 \quad \text{o} \quad y_D = -3 $$

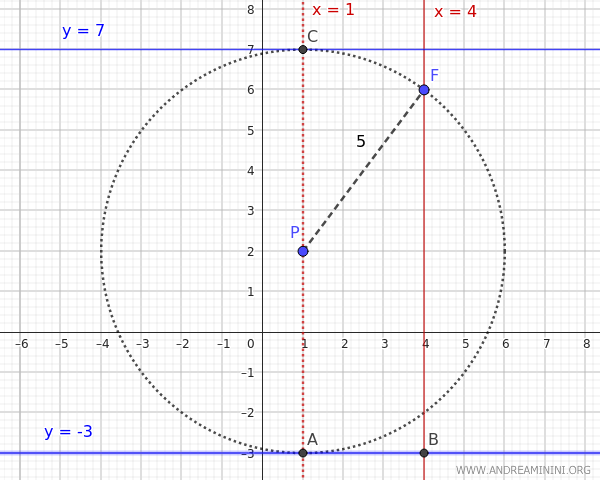
Veamos qué ocurre en cada caso:

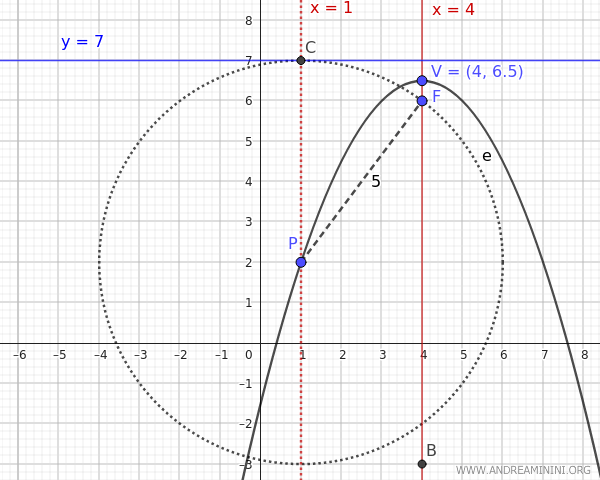
• Si \( y_D = 7 \), el vértice se encuentra en el punto medio entre el foco \( F(4,6) \) y la directriz \( y = 7 \): $$ V(h,k) = \left(4, \frac{6 + 7}{2} \right) = (4, 6.5) $$ Entonces: $$ p = y_F - k = 6 - 6.5 = -0.5 $$ Y la ecuación de la parábola es: $$ (x - 4)^2 = 4p(y - k) = 4 \cdot (-0.5)(y - 6.5) = -2(y - 6.5) $$
  
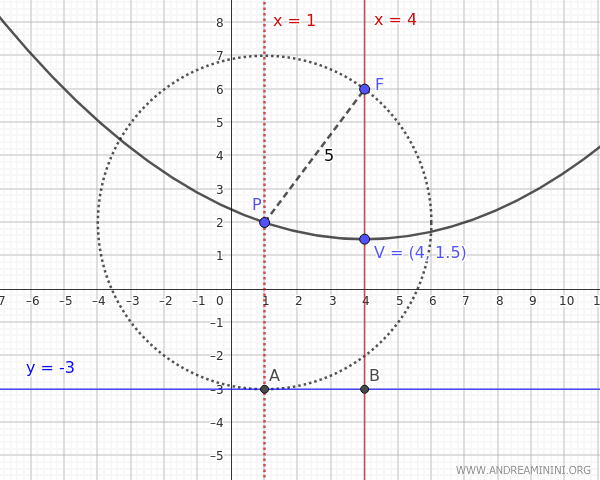
• Si \( y_D = -3 \), el vértice se halla en el punto medio entre el foco y la directriz: $$ V(h,k) = \left(4, \frac{6 + (-3)}{2} \right) = (4, 1.5) $$ Entonces: $$ p = y_F - k = 6 - 1.5 = 4.5 $$ Y la ecuación de la parábola es: $$ (x - 4)^2 = 4p(y - k) = 4 \cdot 4.5(y - 1.5) = 18(y - 1.5) $$
  

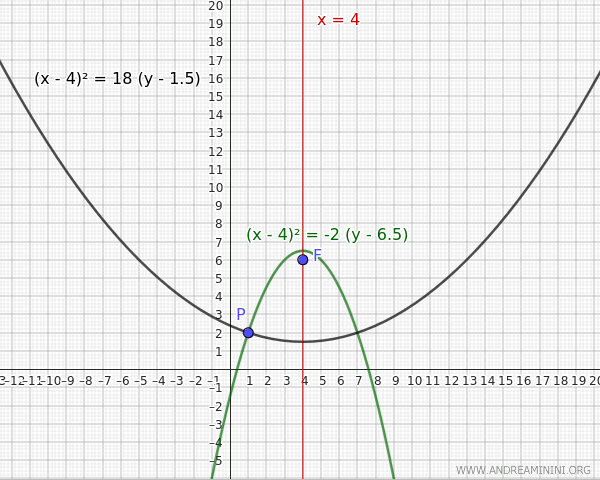
En ausencia de más información, ambas opciones son válidas: la parábola podría abrir tanto hacia arriba como hacia abajo.

2] Parábola con eje de simetría horizontal

Tenemos el punto \( P(x_0, y_0) = (1, 2) \) y el foco \( (x_F, y_F) = (4, 6) \). Si la parábola tiene eje de simetría horizontal, procedemos del siguiente modo:

La ecuación estándar de una parábola con eje paralelo al eje \(x\) es:

$$ (y-k)^2 = 4p(x-h) $$

Como el foco y el vértice se encuentran sobre el eje de simetría horizontal, comparten la misma coordenada \(y\): \( (h, k) = (h, 6) \), por tanto \(k = 6\).

$$ (y-6)^2 = 4p(x-h) $$

Sustituimos las coordenadas del punto \(P = (1, 2)\):

$$ (2 - 6)^2 = 4p(1 - h) $$

$$ 16 = 4p(1 - h) $$

La distancia \(p\) entre el vértice y el foco es: \( p = x_F - h = 4 - h \)

Reemplazamos \(p\):

$$ 16 = 4(4 - h)(1 - h) $$

Desarrollamos el producto:

$$ 16 = 4(4 - 5h + h^2) $$

$$ 16 = 16 - 20h + 4h^2 $$

$$ 4h^2 - 20h = 0 $$

$$ h(4h - 20) = 0 $$

Las soluciones son: \( h = 0 \) y \( h = 5 \).

Estudiamos ambos casos:

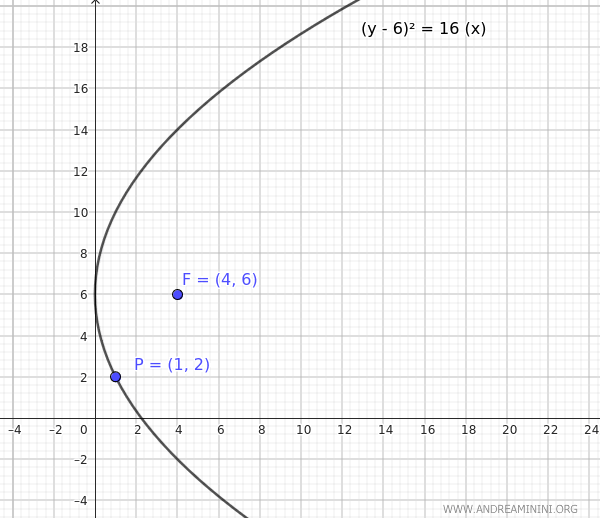
• Si \( h = 0 \), entonces \(p = 4\). La ecuación de la parábola es: $$ (y - 6)^2 = 4 \cdot 4 \cdot x = 16x $$ Como \(p > 0\), la parábola se abre hacia la derecha.
  
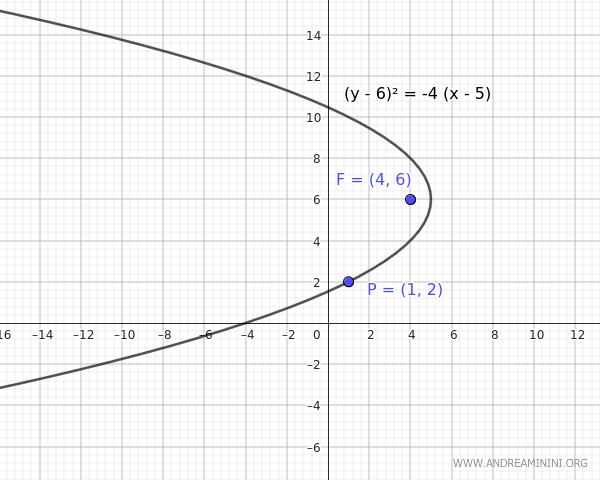
• Si \( h = 5 \), entonces \(p = -1\). La ecuación de la parábola es: $$ (y - 6)^2 = 4 \cdot (-1) \cdot (x - 5) = -4(x - 5) $$ Como \(p < 0\), la parábola se abre hacia la izquierda.
  

En ausencia de más información, ambas soluciones son igualmente aceptables.

Y así sucesivamente.