Secciones cónicas

Las secciones cónicas (o simplemente cónicas) son una familia de curvas planas que se generan al intersectar un cono circular recto con un plano.

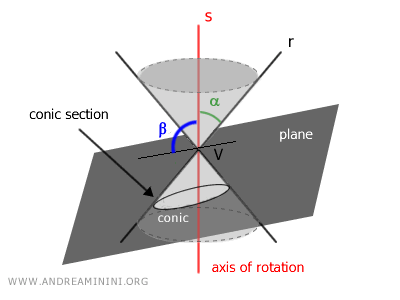
Según la inclinación y la posición del plano respecto al cono, se obtienen distintos tipos de curvas: elipses, parábolas e hipérbolas.

En términos generales, una sección cónica es un lugar geométrico de puntos en el plano que satisface la siguiente ecuación de segundo grado:

$$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $$

donde al menos uno de los coeficientes A, B o C es distinto de cero.

Al evaluar el discriminante de una ecuación cuadrática, es posible determinar la naturaleza de sus soluciones.

$$ \Delta = B^2 - 4AC $$

• Si $ \Delta < 0 $, la ecuación describe una elipse o una circunferencia.
• Si $ \Delta = 0 $, la ecuación describe una parábola.
• Si $ \Delta > 0 $, la ecuación describe una hipérbola.

En la práctica, este criterio resulta muy útil para identificar el tipo geométrico general (elíptico, parabólico o hiperbólico). No obstante, por sí solo no garantiza la existencia de soluciones reales, es decir, que la curva pueda representarse efectivamente en el plano, ni descarta la posibilidad de que se trate de un caso degenerado.

Los antiguos griegos fueron los primeros en descubrir que ciertas curvas podían obtenerse como secciones de un cono. Durante el periodo helenístico, hacia el año 200 a.C., Menecmo y Apolonio de Perge estudiaron a fondo estas curvas. Fue Apolonio quien las clasificó y les dio nombre: elipse, parábola e hipérbola, considerando al círculo como un caso particular de la elipse. Al principio, se utilizaban distintos conos y planos para generar cada tipo de curva, pero Apolonio demostró que todas podían obtenerse a partir de un único cono (ya fuera recto u oblicuo), simplemente variando la inclinación del plano de intersección.

Características de una sección cónica

Para generar una cónica, se consideran dos rectas r y s que se cortan formando un ángulo α (llamado semiapertura) en un punto V del espacio, conocido como vértice.

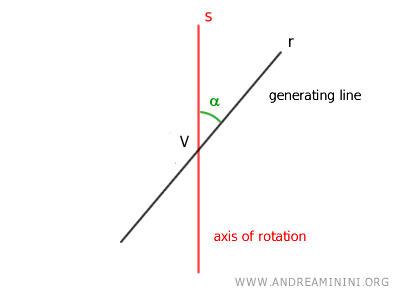
La rotación completa de la recta r en torno a la recta s da lugar a una superficie cónica de dos hojas.

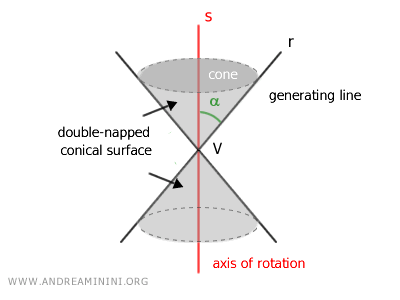
Por este motivo, r se denomina generatriz y s se conoce como eje de rotación.

El espacio delimitado por esta superficie se conoce como cono de dos hojas.

A continuación, se corta el cono con un plano que forma un ángulo β con respecto al eje de simetría.

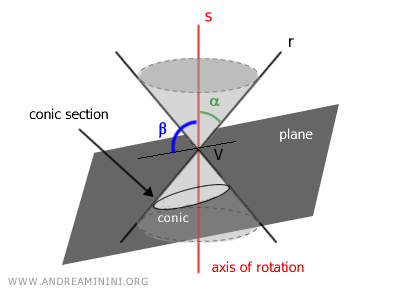
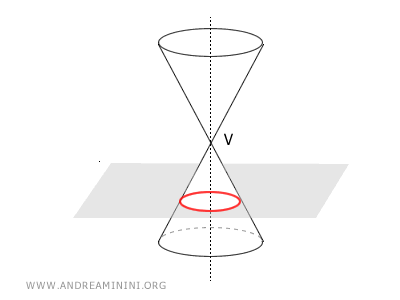
Los puntos de intersección entre el plano y el cono definen una curva llamada sección cónica o simplemente cónica.

Por ejemplo, la cónica representada en la figura anterior aparece en el plano del siguiente modo:

Según la relación entre el ángulo α del cono y el ángulo β del plano, se obtienen distintas curvas, abiertas o cerradas:

• Si β < α, la sección es una hipérbola: una curva abierta formada por dos ramas infinitas, ya que el plano corta ambas hojas del cono.
  
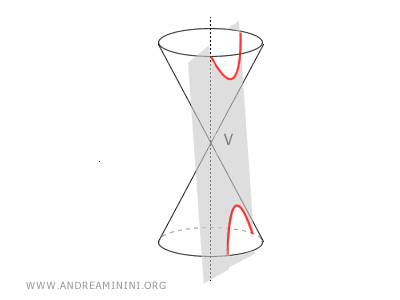
• Si β = α, se obtiene una parábola: una curva abierta de una sola rama, generada cuando el plano tiene la misma inclinación que la generatriz y corta solo una hoja del cono.
  
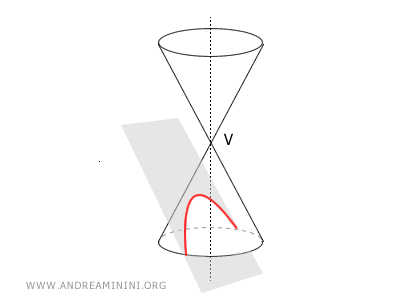
• Si β > α, la sección es una elipse: una curva cerrada y acotada que se forma cuando el plano corta una sola hoja del cono con un ángulo mayor que la semiapertura.
  

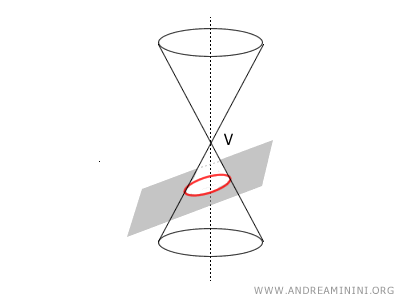
  Ejemplo
  

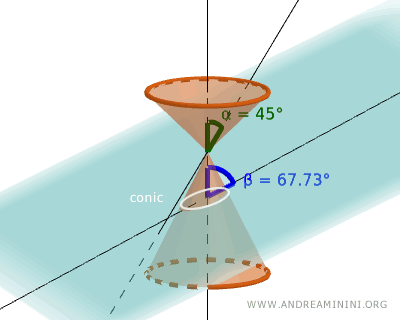
• Si β = π/2, es decir, el plano es perpendicular al eje del cono (ángulo recto de 90°), la cónica es un círculo: una curva cerrada cuyos puntos están todos a la misma distancia de su centro.
  

Tipos de secciones cónicas

Las cónicas se clasifican según su forma y propiedades geométricas:

• Elipse
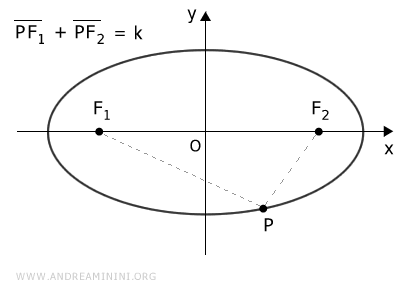
  La elipse es una curva cerrada que se obtiene al cortar un cono con un plano inclinado entre θ y π/2 respecto a su eje. Se define como el conjunto de puntos cuya suma de distancias a dos focos fijos es constante. Tiene dos ejes de simetría: uno mayor y otro menor. Si ambos son iguales, la curva resultante es un círculo.
  
• Parábola
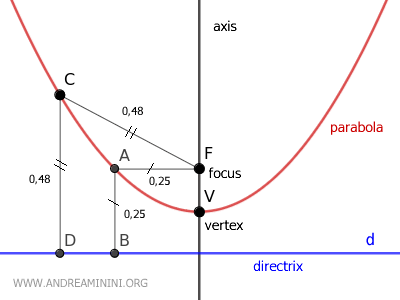
  La parábola es el conjunto de puntos equidistantes de un foco (F) y una directriz (d). Tiene un eje de simetría y se obtiene al cortar un cono con un plano paralelo a una de sus generatrices, formando un ángulo θ con respecto al eje. Es una curva abierta y pertenece a una sola hoja del cono.
  
• Hipérbola
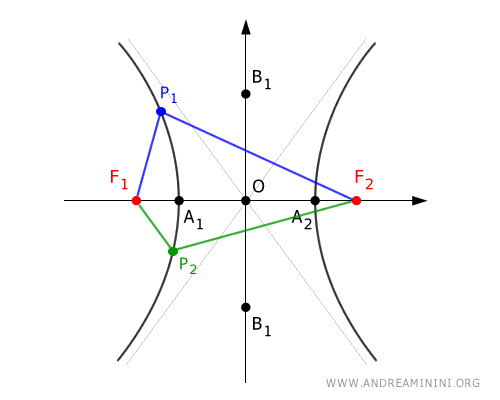
  La hipérbola se genera al cortar un cono con un plano cuya inclinación es menor que θ respecto al eje del cono. Está definida como el conjunto de puntos cuya diferencia absoluta de distancias a dos focos fijos es constante. Es una curva abierta, con dos ramas opuestas que pertenecen a distintas hojas del cono y presenta dos ejes de simetría.
  
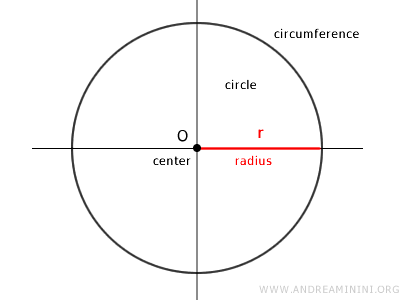
• Círculo
  El círculo es un caso particular de la elipse que se obtiene al cortar un cono recto con un plano perpendicular a su eje. Es una curva cerrada, perfectamente simétrica y equidistante de su centro.
  

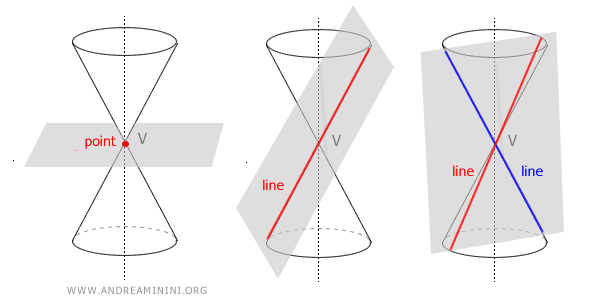
Nota. Estas curvas se denominan “cónicas no degeneradas” para diferenciarlas de las llamadas “cónicas degeneradas”, como un punto, una recta o un par de rectas. Por ejemplo, un punto puede considerarse una cónica degenerada cuando el plano pasa por el vértice del cono. Del mismo modo, una intersección que genera una recta o dos rectas también se clasifica como caso degenerado.

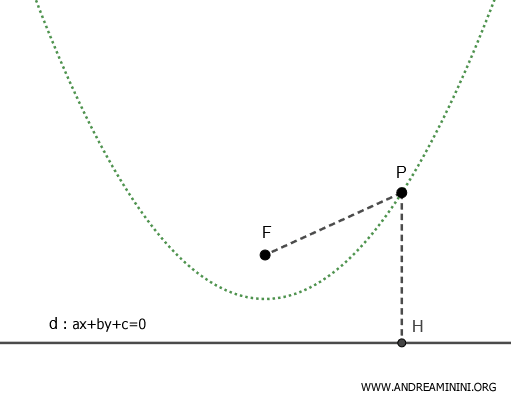
Definición de una sección cónica

Para todo punto $ P(x;y) $ perteneciente a una sección cónica, existe una razón constante $$ \frac{ \overline{PF} }{ \overline{PH} } = e $$ donde PF es la distancia entre el punto P y un punto fijo $ F(p;q) $, llamado foco, y PH es la distancia entre P y una recta fija d: $ ax+by+c=0 $, denominada directriz, que no pasa por P.

La constante “e” es un número real no negativo que representa la excentricidad de la cónica.

El valor de la excentricidad determina el tipo de curva:

• Si e = 0, la cónica es un círculo.
• Si 0 < e < 1, se trata de una elipse.
• Si e = 1, es una parábola.
• Si e > 1, corresponde a una hipérbola.

Nota. Una parábola tiene un único foco y una sola directriz. En cambio, la elipse y la hipérbola poseen dos focos y dos directrices, dispuestas simétricamente con respecto al centro y perpendiculares al eje focal. Por su parte, el círculo puede interpretarse como una cónica cuya directriz se encuentra a una distancia infinita del centro. Técnicamente, no tiene una sola directriz, sino infinitas, todas situadas a distancia infinita.

Ejemplo

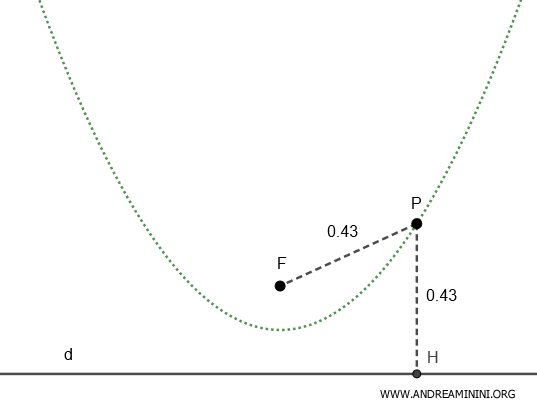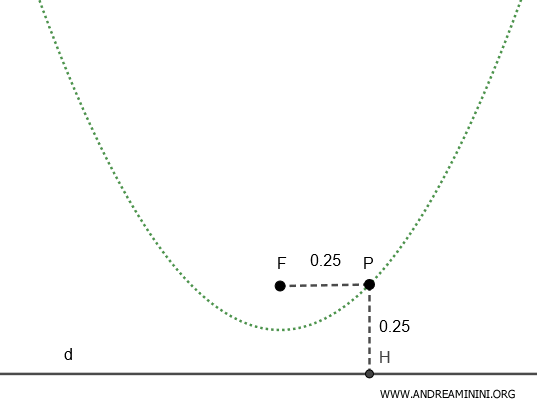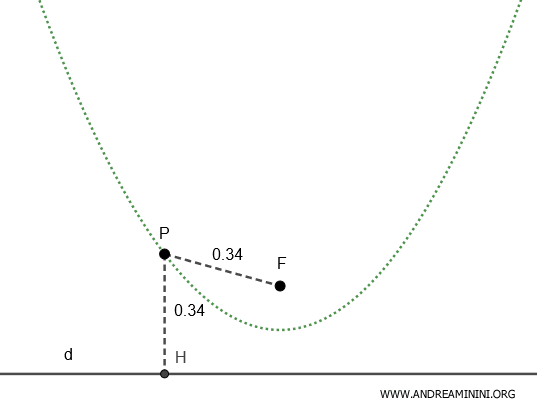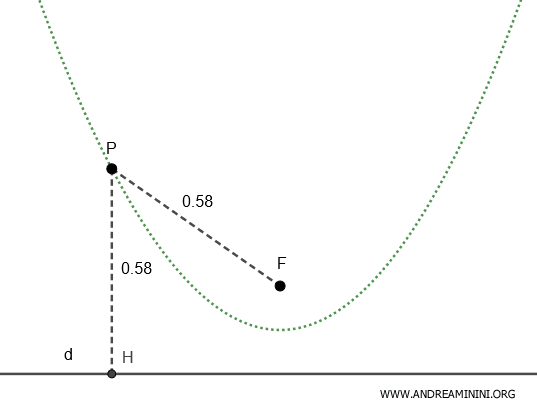
En una parábola, la excentricidad es $ e = 1 $.

$$ e = 1 $$

Esto significa que, para cualquier punto P de la parábola, la distancia al foco F es igual a la distancia a la directriz d.

$$ \frac{ \overline{PF} }{ \overline{PH} } = 1 \quad \Rightarrow \quad \overline{PF} = \overline{PH} $$

La relación entre ambas distancias se mantiene siempre igual a 1.

Ejemplo 2

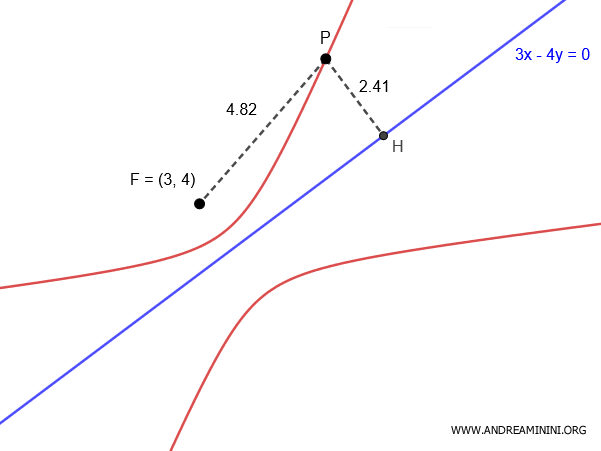
Supongamos que el foco se encuentra en el punto $ F(3;4) $ y que la directriz es la recta $ 3x - 4y = 0 $.

Queremos determinar el lugar geométrico de los puntos $ P(x;y) $ cuya excentricidad sea $ e = 2 $.

$$ e = 2 \quad \Rightarrow \quad \overline{PF} = 2 \cdot \overline{PH} $$

La distancia entre P y F es:

$$ \overline{PF} = \sqrt{(x - 3)^2 + (y - 4)^2} $$

La distancia desde P a la directriz se calcula mediante la fórmula:

$$ \overline{PH} = \frac{|3x - 4y|}{\sqrt{3^2 + (-4)^2}} = \frac{|3x - 4y|}{5} $$

Sustituimos ambas expresiones en la ecuación de la excentricidad:

$$ \sqrt{(x - 3)^2 + (y - 4)^2} = 2 \cdot \frac{|3x - 4y|}{5} $$

Elevamos al cuadrado ambos miembros:

$$ (x - 3)^2 + (y - 4)^2 = \frac{4(3x - 4y)^2}{25} $$

Desarrollando ambos lados:

$$ x^2 - 6x + 9 + y^2 - 8y + 16 = \frac{36x^2 - 96xy + 64y^2}{25} $$

Multiplicamos por 25 para eliminar el denominador:

$$ 25x^2 + 25y^2 - 150x - 200y + 625 = 36x^2 - 96xy + 64y^2 $$

Reorganizando los términos en un solo lado:

$$ -11x^2 + 96xy - 39y^2 - 150x - 200y + 625 = 0 $$

Esta es la ecuación general de la cónica cuya excentricidad es 2.

Ecuación general de una cónica

Una sección cónica puede describirse mediante la ecuación general de segundo grado: $$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $$ donde no todos los coeficientes A, B, C, D, E y F son simultáneamente cero.

Algunos casos particulares:

• Si B = 0 y A = 0 → parábola con eje paralelo al eje x: $$ Cy^2 + Dx + Ey + F = 0 $$
• Si B = 0 y C = 0 → parábola con eje paralelo al eje y: $$ Ax^2 + Dx + Ey + F = 0 $$
• Si B = 0 y A = C ≠ 0 → círculo: $$ Ax^2 + Ay^2 + Dx + Ey + F = 0 $$
• Si B = 0 y A ≠ C, con A·C > 0 → elipse; si A·C < 0 → hipérbola.

En todos estos casos: $$ Ax^2 + Cy^2 + Dx + Ey + F = 0 $$

Explicación. Comenzamos agrupando los términos en \( x \) y \( y \): $$ Ax^2 + Cy^2 + Dx + Ey + F = 0 $$ $$ A \left( x^2 + \frac{D}{A}x \right) + C \left( y^2 + \frac{E}{C}y \right) + F = 0 $$ A continuación, completamos el cuadrado en ambos grupos: $$ A \left( x^2 + \frac{D}{A}x + \left( \frac{D}{2A} \right)^2 - \left( \frac{D}{2A} \right)^2 \right) + C \left( y^2 + \frac{E}{C}y + \left( \frac{E}{2C} \right)^2 - \left( \frac{E}{2C} \right)^2 \right) + F = 0 $$ $$ A \left( x^2 + \frac{D}{A}x + \frac{D^2}{4A^2} \right) + C \left( y^2 + \frac{E}{C}y + \frac{E^2}{4C^2} \right) + F - \frac{D^2}{4A} - \frac{E^2}{4C} = 0 $$ $$ A \left( x + \frac{D}{2A} \right)^2 + C \left( y + \frac{E}{2C} \right)^2 = \frac{D^2}{4A} + \frac{E^2}{4C} - F $$ Podemos simplificar esta expresión introduciendo la constante \( s \): $$ A \left( x + \frac{D}{2A} \right)^2 + C \left( y + \frac{E}{2C} \right)^2 = s $$ Esta ecuación también representa la condición de existencia real de una elipse o una hipérbola, es decir, cuando \( s > 0 \): $$ s = \frac{D^2}{4A} + \frac{E^2}{4C} - F $$ De hecho, una elipse solo existe si \( s > 0 \); si \( s = 0 \), la elipse degenera en un punto, y si \( s < 0 \), no existe. Para una hipérbola, el valor de \( s \) puede ser positivo o negativo, dependiendo de si su eje real es paralelo al eje \( x \) o al eje \( y \), pero no puede ser cero, ya que en ese caso la hipérbola degenera en dos rectas secantes. Volviendo a la ecuación: $$ A \left( x + \frac{D}{2A} \right)^2 + C \left( y + \frac{E}{2C} \right)^2 = s $$ Podemos interpretarla como una traslación del centro de la cónica desde el origen \( (0, 0) \) al punto $$ \left( - \frac{D}{2A}, - \frac{E}{2C} \right) $$ lo que nos conduce a la forma canónica: $$ Ax^2 + Cy^2 = s $$ Dependiendo del signo de \( A \) y \( C \), esta ecuación representa una elipse (si tienen el mismo signo) o una hipérbola (si tienen signos opuestos).

Ejemplo

Consideremos la siguiente ecuación de segundo grado:

$$ -2x^2 + y^2 - 6x - 5y + 3 = 0 $$

Queremos determinar si esta ecuación representa una sección cónica.

En este caso, los coeficientes son: A = -2, B = 0, C = 1, D = -6, E = -5, F = 3.

Dado que B = 0 y A ≠ C, y además A·C < 0 (los coeficientes cuadráticos tienen signos opuestos), podemos concluir que se trata de una hipérbola.

Procedamos al completado de cuadrados:

$$ (-2x^2 - 6x) + (y^2 - 5y) + 3 = 0 $$

$$ -2(x^2 + 3x) + (y^2 - 5y) + 3 = 0 $$

$$ -2(x^2 + 3x + \left(\frac{3}{2}\right)^2 - \left(\frac{3}{2}\right)^2) + (y^2 - 5y + \left(\frac{5}{2}\right)^2 - \left(\frac{5}{2}\right)^2) + 3 = 0 $$

$$ -2\left(x + \frac{3}{2}\right)^2 + \left(y - \frac{5}{2}\right)^2 + 3 + \frac{9}{2} - \frac{25}{4} = 0 $$

$$ -2\left(x + \frac{3}{2}\right)^2 + \left(y - \frac{5}{2}\right)^2 + \frac{12 + 18 - 25}{4} = 0 $$

$$ -2\left(x + \frac{3}{2}\right)^2 + \left(y - \frac{5}{2}\right)^2 + \frac{5}{4} = 0 $$

$$ -2\left(x + \frac{3}{2}\right)^2 + \left(y - \frac{5}{2}\right)^2 = -\frac{5}{4} $$

Multiplicamos ambos lados por -1:

$$ 2\left(x + \frac{3}{2}\right)^2 - \left(y - \frac{5}{2}\right)^2 = \frac{5}{4} $$

Esta es la ecuación canónica de una hipérbola con centro en $ \left( -\frac{3}{2}, \frac{5}{2} \right) $, cuyo eje transversal - el que contiene a los focos - es paralelo al eje X.

Ejemplo 2

Analicemos ahora otra ecuación de segundo grado:

$$ 4x^2 + 9y^2 - 5x - y + 10 = 0 $$

Queremos establecer si corresponde a una sección cónica.

Los coeficientes son: A = 4, B = 0, C = 9, D = -5, E = -1, F = 10.

Como A y C son positivos, distintos entre sí y no nulos, y su producto A·C > 0, esto sugiere que podría tratarse de una elipse.

Agrupamos los términos semejantes:

$$ (4x^2 - 5x) + (9y^2 - y) + 10 = 0 $$

Completamos cuadrados:

$$ 4\left(x^2 - \frac{5}{4}x + \left(\frac{5}{8}\right)^2 - \left(\frac{5}{8}\right)^2 \right) + 9\left(y^2 - \frac{1}{9}y + \left(\frac{1}{18}\right)^2 - \left(\frac{1}{18}\right)^2 \right) + 10 = 0 $$

$$ 4\left(x - \frac{5}{8}\right)^2 - \frac{25}{16} + 9\left(y - \frac{1}{18}\right)^2 - \frac{1}{36} + 10 = 0 $$

$$ 4\left(x - \frac{5}{8}\right)^2 + 9\left(y - \frac{1}{18}\right)^2 = -\left(10 - \frac{25}{16} - \frac{1}{36}\right) $$

$$ 4\left(x - \frac{5}{8}\right)^2 + 9\left(y - \frac{1}{18}\right)^2 = -\frac{1211}{144} $$

En este caso, el segundo miembro es negativo, lo cual viola la condición de existencia de una elipse:

$$ s = -\frac{1211}{144} < 0 $$

Por lo tanto, esta ecuación no representa una sección cónica real.

Demostración

Consideremos una recta directriz definida por \( ax + by + c = 0 \), y un punto arbitrario \( P(x, y) \) que no pertenece a dicha recta.

Por definición, una cónica es el lugar geométrico de los puntos \( P(x, y) \) del plano cuya razón entre la distancia a un punto fijo \( F(p, q) \), llamado foco, y la distancia a una recta fija \( d \), denominada directriz, es constante. Esta constante se conoce como excentricidad \( e \):

$$ \frac{ \overline{PF} }{ \overline{PH} } = e $$

lo que equivale a:

$$ \overline{PF} = e \cdot \overline{PH} $$

La distancia euclidiana entre el punto \( P(x, y) \) y el foco \( F(p, q) \) está dada por:

$$ \overline{PF} = \sqrt{(x - p)^2 + (y - q)^2} $$

Mientras que la distancia perpendicular desde \( P(x, y) \) a la recta directriz \( ax + by + c = 0 \) es:

$$ \overline{PH} = \frac{|ax + by + c|}{\sqrt{a^2 + b^2}} $$

Sustituyendo ambas expresiones en la definición:

$$ \sqrt{(x - p)^2 + (y - q)^2} = e \cdot \frac{|ax + by + c|}{\sqrt{a^2 + b^2}} $$

Elevando al cuadrado ambos miembros:

$$ (x - p)^2 + (y - q)^2 = \frac{e^2}{a^2 + b^2} \cdot (ax + by + c)^2 $$

Desarrollando ambos lados de la ecuación:

$$ x^2 - 2px + p^2 + y^2 - 2qy + q^2 = \frac{e^2}{a^2 + b^2} \left( a^2x^2 + 2abxy + b^2y^2 + 2acx + 2bcy + c^2 \right) $$

Reagrupando los términos y trasladando todo a un solo miembro, obtenemos la forma general:

$$ [(1 - e^2)a^2 + b^2]x^2 + 2abe^2xy + [(1 - e^2)b^2 + a^2]y^2 $$

$$ - 2(a^2p + b^2p + ace)x - 2(a^2q + b^2q + bce)y $$

$$ + (p^2 + q^2)(a^2 + b^2) - c^2e^2 = 0 $$

Esta expresión se puede escribir en la forma general de una cónica:

$$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $$

donde los coeficientes están dados en función de los parámetros \( a \), \( b \), \( c \), \( p \), \( q \) y \( e \):

• $ A = (1 - e^2)a^2 + b^2 $
• $ B = 2abe^2 $
• $ C = (1 - e^2)b^2 + a^2 $
• $ D = -2(a^2p + b^2p + ace) $
• $ E = -2(a^2q + b^2q + bce) $
• $ F = (p^2 + q^2)(a^2 + b^2) - c^2e^2 $

Esta ecuación representa una sección cónica cuyo tipo depende del valor de la excentricidad \( e \):

• Si \( e = 0 \), se trata de una circunferencia.
• Si \( 0 < e < 1 \), es una elipse.
• Si \( e = 1 \), es una parábola.
• Si \( e > 1 \), se trata de una hipérbola.

En resumen, a partir de la definición métrica de cónica y utilizando las fórmulas de distancia, hemos deducido su ecuación general en el plano cartesiano.

Cónicas Imaginarias y Degeneradas

La ecuación general de segundo grado \[ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0, \qquad (A,B,C \ \text{no todos nulos}) \] se clasifica a partir del discriminante \(\Delta = B^2 - 4AC\).

Este discriminante permite distinguir tres grandes familias de cónicas:

• si \(\Delta < 0\), la curva es de tipo elíptico (elipse o circunferencia);
• si \(\Delta = 0\), la curva es parabólica (parábola);
• si \(\Delta > 0\), la curva es hiperbólica (hipérbola).

No obstante, el discriminante por sí solo no es suficiente: no garantiza la existencia de soluciones reales ni excluye los casos degenerados.

Dicho de otro modo, el discriminante únicamente indica a qué familia pertenece la ecuación (elíptica, parabólica o hiperbólica). No determina si la cónica es imaginaria (sin puntos reales en el plano cartesiano) ni si se reduce a un conjunto de rectas.

Por ejemplo, con \(\Delta < 0\) puede surgir tanto una elipse real como una elipse imaginaria (sin puntos reales). Con \(\Delta = 0\) puede aparecer no solo una parábola, sino también un par de rectas paralelas. Con \(\Delta > 0\) una hipérbola puede degenerar en dos rectas reales secantes.

Para identificar los casos degenerados se recurre a la matriz simétrica asociada a la ecuación:

\[ Q = \begin{pmatrix} A & B/2 & D/2 \\ B/2 & C & E/2 \\ D/2 & E/2 & F \end{pmatrix}. \]

Su determinante actúa como invariante que diferencia las cónicas propias de las degeneradas:

• si \(\det(Q) \neq 0\), la curva es una cónica real y no degenerada (elipse, parábola o hipérbola);
• si \(\det(Q) = 0\), la ecuación representa una cónica degenerada, es decir, un sistema de rectas (secantes, paralelas o imaginarias, según el signo de \(\Delta\)).

El determinante de la matriz simétrica indica, por tanto, si la cónica se degenera (en un par de rectas reales, paralelas o imaginarias) o no.

Nota. El determinante de (Q) solo determina si la cónica es degenerada o no; no asegura la existencia de puntos reales. Incluso cuando \( \det(Q) \neq 0 \), la cónica puede ser imaginaria -una ecuación sin soluciones reales (por ejemplo \(x^2 + y^2 + 1 = 0\))- y por tanto invisible en el plano cartesiano. Para comprobar si la cónica puede representarse gráficamente, es necesario verificar si la ecuación admite soluciones reales, es decir, si existen valores reales de (x) e (y) que la satisfacen.

Ejemplos de Clasificación de Cónicas

Ejemplo 1 (elipse real)

Consideremos la ecuación

\[ x^2 + 2y^2 - 4 = 0 \]

Aquí \(A=1\), \(B=0\), \(C=2\). El discriminante es

$$ \Delta = 0^2 - 4\cdot 1 \cdot 2 = -8 < 0 $$

En consecuencia, la cónica es de tipo elíptico. La ecuación tiene soluciones reales y describe una elipse con semiejes \(\sqrt{4}\) y \(\sqrt{2}\).

Ejemplo 2 (elipse imaginaria, sin puntos reales)

Tomemos ahora la ecuación

\[ x^2 + y^2 + 1 = 0 \]

Aquí \(A=1\), \(B=0\), \(C=1\). El discriminante es

$$ \Delta = 0 - 4 \cdot 1 \cdot 1 = -4 < 0 $$

La curva es elíptica, pero la ecuación carece de soluciones reales: se trata de una elipse imaginaria.

¿Qué es una cónica imaginaria? En términos sencillos, una cónica imaginaria es una curva que “existe” algebraicamente como ecuación pero no se manifiesta en el plano cartesiano, ya que no hay puntos reales que representar. Es, por lo tanto, un objeto puramente algebraico y no geométrico.

Ejemplo 3 (parábola)

Consideremos la ecuación

\[ y - x^2 = 0 \]

Aquí \(A=1\), \(B=0\), \(C=0\). El discriminante es

$$ \Delta = 0^2 - 4\cdot 1 \cdot 0 = 0 $$

Así, la cónica es parabólica. La ecuación describe una parábola con eje vertical.

Ejemplo 4 (par de rectas paralelas)

Consideremos la ecuación

\[ x^2 - 1 = 0 \]

Los coeficientes son \(A=1\), \(B=0\), \(C=0\), \(D=0\), \(E=0\), \(F=-1\). El discriminante es

\[ \Delta = B^2 - 4AC = 0^2 - 4 \cdot 1 \cdot 0 = 0 \]

La curva es, por tanto, parabólica.

La matriz asociada \(Q\) es

\[ Q = \begin{pmatrix} A & B/2 & D/2 \\ B/2 & C & E/2 \\ D/2 & E/2 & F \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & -1 \end{pmatrix} \]

Su determinante es

\[ \det(Q) = \begin{vmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & -1 \end{vmatrix} = 1 \cdot (0 \cdot -1 - 0 \cdot 0) = 0 \]

Como \(\det(Q) = 0\), la cónica resulta degenerada. De hecho, la ecuación se factoriza como

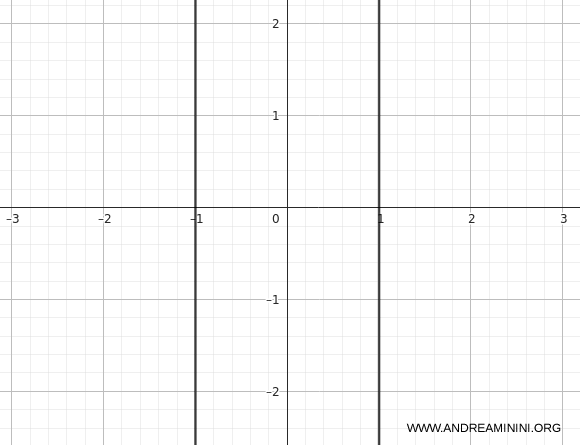
\[ x^2 - 1 = (x-1)(x+1) = 0 \]

La curva no es una parábola sino un par de rectas verticales paralelas \(x=1\) y \(x=-1\).

Ejemplo 5 (hipérbola)

Consideremos la ecuación

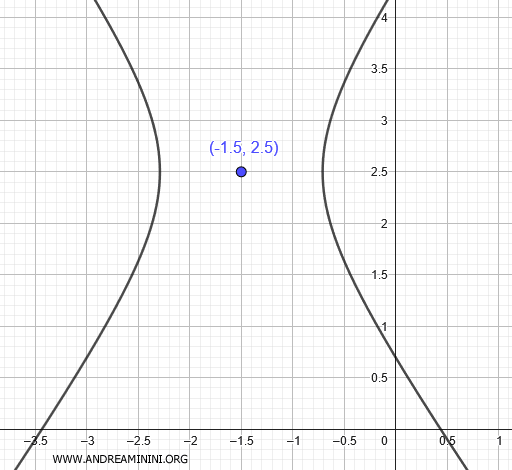
\[ x^2 - y^2 - 1 = 0 \]

Aquí \(A=1\), \(B=0\), \(C=-1\). El discriminante es \(\Delta = 0 - 4\cdot 1 \cdot (-1) = 4 > 0\), por lo que la curva es hiperbólica.

La ecuación describe una hipérbola con asíntotas \(y = \pm x\).

Ejemplo 6 (par de rectas secantes reales)

Consideremos la ecuación

\[ x^2 - y^2 = 0 \]

Los coeficientes son \(A=1\), \(B=0\), \(C=-1\), \(D=0\), \(E=0\), \(F=0\).

El discriminante es

\[ \Delta = B^2 - 4AC = 0^2 - 4 \cdot 1 \cdot (-1) = 4 > 0 \]

Así pues, la curva es hiperbólica.

La matriz asociada es

\[ Q = \begin{pmatrix} A & B/2 & D/2 \\ B/2 & C & E/2 \\ D/2 & E/2 & F \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 0 \end{pmatrix} \]

El determinante resulta nulo:

\[ \det(Q) = \begin{vmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 0 \end{vmatrix} = 1 \cdot (-1) \cdot 0 = 0 \]

Como \(\det(Q) = 0\), la cónica se degenera en dos rectas. En efecto, la ecuación se factoriza como

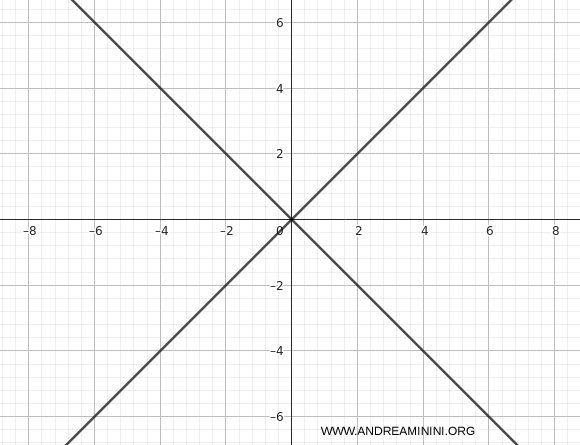
\[ x^2 - y^2 = (x-y)(x+y) = 0 \]

La curva no es una hipérbola propiamente dicha, sino un par de rectas reales secantes \(y=x\) y \(y=-x\).

Notas adicionales

Algunas consideraciones complementarias sobre las secciones cónicas.

• Cómo eliminar el término mixto xy en la ecuación de una cónica
  El término mixto $ xy $ en la ecuación de una cónica puede suprimirse mediante una rotación de los ejes coordenados en un ángulo $ \alpha $ que verifique la condición $$ \tan 2 \alpha = \frac{B}{A-C} $$ donde $ A, B, C $ son los coeficientes de la ecuación general de la cónica.

  Nota. Si el denominador $ A-C=0 $, entonces $\tan 2\alpha$ no está definido porque corresponde a un ángulo vertical. En este caso particular, la condición se reduce a $\cos 2\alpha = 0$, lo que implica $2\alpha = \pi/2 + k\pi$. 

Y así sucesivamente...