Radio focal en una sección cónica

El radio focal en una sección cónica es el segmento que une un punto cualquiera \( P \) de la curva con uno de sus focos \( F \).

Las secciones cónicas incluyen curvas bien conocidas como la elipse, la parábola y la hipérbola. Estas curvas, también llamadas simplemente “cónicas”, se obtienen al cortar un cono mediante un plano en distintas posiciones.

Para comprender mejor el concepto de radio focal, veamos cómo se manifiesta en los distintos tipos de secciones cónicas:

• Parábola
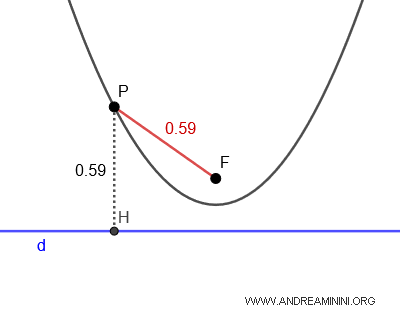
  La parábola tiene un único foco \( F \). Por lo tanto, a cada punto \( P \) de la parábola le corresponde un solo radio focal \( \overline{PF} \). Además, cualquier punto \( P \) se encuentra a igual distancia del foco \( F \) y de la directriz \( d \).
  
• Elipse
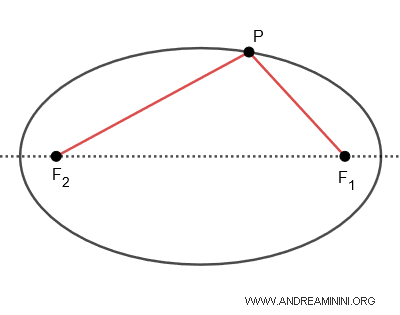
  La elipse posee dos focos, \( F_1 \) y \( F_2 \). En consecuencia, cada punto \( P \) de la curva determina dos radios focales: \( \overline{PF_1} \) y \( \overline{PF_2} \). En toda elipse, la suma de las distancias desde un punto cualquiera \( P \) a ambos focos es constante: \( \overline{PF_1} + \overline{PF_2} = k \).
  
• Hipérbola
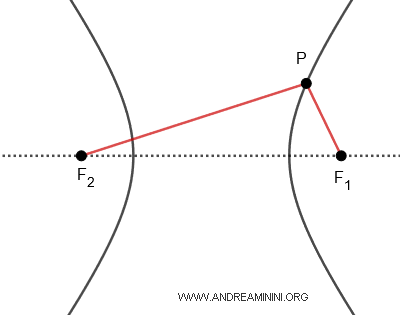
  La hipérbola también cuenta con dos focos, \( F_1 \) y \( F_2 \). Por lo tanto, todo punto \( P \) de la curva define dos radios focales: \( \overline{PF_1} \) y \( \overline{PF_2} \). En este caso, lo que se mantiene constante es la diferencia entre ambas distancias: \( \overline{PF_1} - \overline{PF_2} = k \).
  

En todos los casos, el radio focal representa la distancia entre un punto concreto de la sección cónica (ya sea elipse, parábola o hipérbola) y uno de sus focos.

Este concepto es fundamental porque permite relacionar la geometría de la curva con la posición de sus focos, lo cual explica muchas de sus propiedades ópticas y facilita diversas aplicaciones prácticas.

Por ejemplo, en una elipse, toda onda de luz o sonido que se origina en uno de los focos se refleja pasando exactamente por el otro. Este principio se aplica en numerosos dispositivos ópticos y acústicos. En una parábola, todas las ondas que llegan paralelas al eje de simetría convergen en el foco, lo que justifica el uso de superficies parabólicas en antenas parabólicas, reflectores y faros.

Y así sucesivamente.