Hipérbola Equilátera
Una hipérbola equilátera es un caso particular de hipérbola en el que los ejes transversal y conjugado tienen la misma longitud, es decir, $ a = b $. La ecuación estándar de este tipo de hipérbola es: $$ \frac{x^2}{a^2} - \frac{y^2}{a^2} = \pm 1 $$ que también puede expresarse como $$ x^2 - y^2 = \pm a^2 $$
Esta ecuación describe una curva abierta formada por el conjunto de puntos que satisfacen la igualdad x2 - y2 = a2.
Como en toda hipérbola, cada punto P de la curva mantiene constante la diferencia de distancias a los dos focos, F1 y F2.

Nota: En cualquier hipérbola, incluida la equilátera, la diferencia entre las distancias de un punto P a los focos es siempre igual a 2a. $$ | \overline{PF_1} - \overline{PF_2} | = 2a $$ Aquí, "a" representa la distancia entre un vértice y el centro de la hipérbola. Por ejemplo, si a = 2 y b = 2, entonces la diferencia de distancias es 2a = 4.
Características
La hipérbola equilátera se caracteriza por tener ejes simétricos y de igual longitud.
Esto implica que la distancia desde el centro (O) tanto a los vértices reales (a) como a los vértices conjugados (b) es la misma.
$$ a = b $$
Los vértices reales (a) son los puntos donde la hipérbola corta el eje transversal, mientras que los vértices conjugados (b) corresponden a los puntos de intersección con el eje conjugado (también llamado eje normal).
Como $ 2a = 2b $, los ejes transversal y conjugado forman un cuadrado en lugar de un rectángulo, y las asíntotas coinciden con las diagonales de ese cuadrado.

En la hipérbola equilátera, las asíntotas son perpendiculares entre sí y coinciden con las bisectrices de los cuadrantes del plano cartesiano.
$$ y = x $$
$$ y = -x $$
Además, los focos se ubican sobre el eje transversal, a una distancia del centro igual a $ c = \sqrt{a^2 + b^2} $, donde "a" y "b" son las distancias del centro O a los vértices reales y conjugados, respectivamente.
$$ c = \sqrt{a^2 + b^2} $$
Si el eje transversal es el eje x, las coordenadas de los focos son:
$$ F_1(-c;0) \\ F_2(c;0) $$
Si el eje transversal es el eje y, las coordenadas de los focos son:
$$ F_1(0;-c) \\ F_2(0;c) $$
En el caso de la hipérbola equilátera, la distancia focal $ c $ se simplifica de la siguiente manera:
$$ c = \sqrt{a^2 + a^2} = \sqrt{2a^2} = a \sqrt{2} $$
Como consecuencia, la excentricidad de la hipérbola se expresa así:
$$ e = \frac{c}{a} = \frac{a \sqrt{2}}{a} = \sqrt{2} $$
Por último, la ecuación canónica de la hipérbola equilátera es:
- Cuando los focos están sobre el eje x: $$ x^2 - y^2 = a^2 $$
- Cuando los focos están sobre el eje y: $$ y^2 - x^2 = a^2 $$
Todo punto perteneciente a una hipérbola equilátera debe cumplir con esta ecuación.
Un Ejemplo Práctico
Veamos un caso concreto de hipérbola equilátera centrada en el origen O(0, 0) del sistema cartesiano:
$$ x^2 - y^2 = 4 $$
En esta ecuación, a2 = 4
$$ a^2 = 4 $$
Al extraer la raíz cuadrada de ambos lados, se obtiene a = 2.
$$ \sqrt{a^2} = \sqrt{4} $$
$$ a = 2 $$
Este valor representa la distancia desde el centro hasta los vértices reales situados sobre el eje transversal A1A2.
$$ A_1(-a, 0) = (-2, 0) $$
$$ A_2(a, 0) = (2, 0) $$
Marcamos en el plano los vértices reales:

Dado que la hipérbola es equilátera, se cumple que a = b, por lo tanto b = 2 también.
Las coordenadas de los vértices sobre el eje conjugado son entonces:
$$ B_1(-b, 0) = (-2, 0) $$
$$ B_2(b, 0) = (2, 0) $$
Marcamos en el plano los vértices conjugados:

Para identificar las diagonales, construimos un cuadrado centrado en el origen cuyos lados miden 2a.
Las diagonales de este cuadrado corresponden a las asíntotas de la hipérbola equilátera.

Con los valores conocidos de "a" y "b", calculamos la distancia "c" desde el centro hasta los focos utilizando el teorema de Pitágoras:
$$ c = \sqrt{a^2 + b^2} $$
$$ c = \sqrt{2^2 + 2^2} = \sqrt{4 + 4} = \sqrt{8} = 2\sqrt{2} \approx 2.83 $$
Las coordenadas de los focos resultan ser:
$$ F_1(-c, 0) = (-2.83, 0) $$
$$ F_2(c, 0) = (2.83, 0) $$
Ubicamos los focos en el plano:

Podemos ahora obtener puntos de la hipérbola a partir de su ecuación canónica:
$$ x^2 - y^2 = a^2 $$
En este caso, a = 2
$$ x^2 - y^2 = 2^2 $$
$$ x^2 - y^2 = 4 $$
Despejando y en función de x:
$$ y^2 = x^2 - 4 $$
$$ \sqrt{y^2} = \sqrt{x^2 - 4} $$
$$ y = \pm \sqrt{x^2 - 4} $$
Esto nos permite calcular las coordenadas (x, y) de puntos de la hipérbola para distintos valores de x en los intervalos (-∞, -2.81] ∪ [2.81, ∞).
| x | y |
|---|---|
| -5 | ±4.58 |
| -4 | ±3.46 |
| -3 | ±2.24 |
| 3 | ±2.24 |
| 4 | ±3.46 |
| 5 | ±4.58 |
Con estas coordenadas, podemos trazar los primeros puntos de la curva en el plano.

Para completar la gráfica, basta con calcular más puntos y unirlos suavemente.
Así obtenemos la hipérbola equilátera completa.

Nota. Como en toda hipérbola, para cualquier punto P de la curva, la diferencia absoluta entre las distancias a los focos es constante y vale 2a = 4.
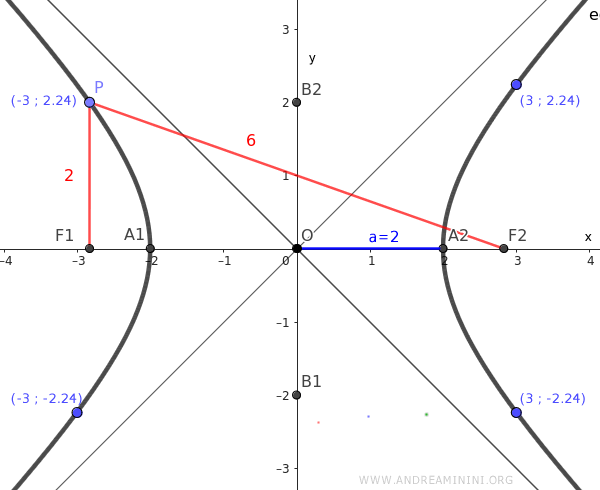
Demostración
Consideremos una hipérbola centrada en el origen O(0, 0), con eje transversal sobre el eje x y eje conjugado sobre el eje y, ambos de la misma longitud.
$$ a = b $$
Como los valores de los semiejes son iguales, el rectángulo ABCD, construido con lados de longitud 2a y 2b y centrado en el origen, se convierte en un cuadrado.

En este caso, las diagonales del cuadrado coinciden con las bisectrices de los cuadrantes del plano cartesiano:
$$ y = x $$
$$ y = -x $$
La ecuación canónica de una hipérbola centrada en el origen, con los focos situados sobre el eje x, es:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
Como a = b, podemos sustituir \( b^2 \) por \( a^2 \):
$$ \frac{x^2}{a^2} - \frac{y^2}{a^2} = 1 $$
$$ \frac{x^2 - y^2}{a^2} = 1 $$
Multiplicando ambos miembros por \( a^2 \), obtenemos:
$$ \left(\frac{x^2 - y^2}{a^2}\right) \cdot a^2 = 1 \cdot a^2 $$
$$ x^2 - y^2 = a^2 $$
Así se obtiene la ecuación canónica de la hipérbola equilátera.
Hipérbola Equilátera con Asíntotas Paralelas a los Ejes Cartesianos
La ecuación de una hipérbola equilátera cuyas asíntotas son paralelas a los ejes coordenados es $$ xy = 1 $$. Si el centro de la hipérbola no se encuentra en el origen, la ecuación se escribe como $$ (x - x_0) \cdot (y - y_0) $$, donde $ x_0 $ y $ y_0 $ son las coordenadas del centro.
Una hipérbola equilátera cuyo eje transversal se encuentra sobre una bisectriz del plano cartesiano puede interpretarse como una rotación de 45 grados de la hipérbola equilátera estándar.

Se trata de un caso particular en el que el eje transversal coincide con una bisectriz de los cuadrantes, en lugar de coincidir con uno de los ejes cartesianos.
En otras palabras, las bisectrices actúan como ejes de la hipérbola, mientras que los ejes cartesianos se convierten en sus asíntotas.
En este sistema rotado, la ecuación de la hipérbola equilátera es:
$$ x \cdot y = k $$
donde \( k \) es una constante, positiva o negativa.
- Si \( k > 0 \), las ramas de la hipérbola se ubican en los cuadrantes primero y tercero.
- Si \( k < 0 \), las ramas se encuentran en los cuadrantes segundo y cuarto.
Los ejes de simetría son las bisectrices:
$$ y = x $$
$$ y = -x $$
La relación entre \( k \) y la longitud del semieje transversal es:
$$ k = \pm \frac{a^2}{2} $$
De donde se deduce que:
$$ a = \overline{OA_1} = \overline{OA_2} = \sqrt{2|k|} $$
Los vértices reales tienen las siguientes coordenadas:
- Si \( k > 0 \): $$ A_1(- \sqrt{k}, - \sqrt{k}) $$ y $$ A_2(\sqrt{k}, \sqrt{k}) $$
- Si \( k < 0 \): $$ A_1(- \sqrt{-k}, \sqrt{-k}) $$ y $$ A_2(\sqrt{-k}, - \sqrt{-k}) $$
La distancia focal es:
$$ c = a \sqrt{2} = \sqrt{2|k|} \cdot \sqrt{2} = 2\sqrt{|k|} $$
Y las coordenadas de los focos son:
- Si \( k > 0 \): $$ F_1(- \sqrt{2k}, - \sqrt{2k}) $$ y $$ F_2(\sqrt{2k}, \sqrt{2k}) $$
- Si \( k < 0 \): $$ F_1(- \sqrt{-2k}, \sqrt{-2k}) $$ y $$ F_2(\sqrt{-2k}, - \sqrt{-2k}) $$
En resumen, cuando \( k > 0 \), el eje transversal es la bisectriz que atraviesa el primer y el tercer cuadrante del plano cartesiano:

Cuando \( k < 0 \), el eje transversal corresponde a la bisectriz del segundo y cuarto cuadrante:

Demostración
Para ilustrar las fórmulas, consideremos dos sistemas de coordenadas: (x, y) y (x', y').
El primero, (x, y), está basado en los ejes cartesianos; el segundo, (x', y'), utiliza como ejes las bisectrices de los cuadrantes.

Por ejemplo, en el sistema cartesiano el punto P tiene coordenadas (x, y), mientras que en el sistema oblicuo sus coordenadas son (x', y').
En el sistema (x', y'), las longitudes de los segmentos AP y BP son:
$$ \overline{AP} = |x'| $$
$$ \overline{BP} = |y'| $$
El producto de estas longitudes es simplemente:
$$ \overline{AP} \cdot \overline{BP} = |x'| \cdot |y'| = |x'y'| $$
Para medir esas mismas distancias en el sistema (x, y), debemos calcular la distancia del punto P a las rectas que definen los ejes x' e y'.
La recta y' corresponde a la bisectriz \( y = x \), es decir \( x - y = 0 \); la recta x' corresponde a \( y = -x \), es decir \( x + y = 0 \).
La distancia de un punto \( P(x_0, y_0) \) a una recta \( ax + by + c = 0 \) está dada por:
$$ d = \frac{|ax_0 + by_0 + c|}{\sqrt{a^2 + b^2}} $$
Aplicando la fórmula a \( x - y = 0 \):
$$ \overline{AP} = \frac{|x - y|}{\sqrt{1^2 + (-1)^2}} = \frac{|x - y|}{\sqrt{2}} $$
Y a \( x + y = 0 \):
$$ \overline{BP} = \frac{|x + y|}{\sqrt{1^2 + 1^2}} = \frac{|x + y|}{\sqrt{2}} $$
El producto de ambas distancias es:
$$ \overline{AP} \cdot \overline{BP} = \frac{|x - y|}{\sqrt{2}} \cdot \frac{|x + y|}{\sqrt{2}} = \frac{|x^2 - y^2|}{2} $$
En una hipérbola equilátera, se cumple \( x^2 - y^2 = a^2 \), por lo que:
$$ \overline{AP} \cdot \overline{BP} = \frac{a^2}{2} $$
Por tanto, en ambos sistemas de coordenadas, el producto \( \overline{AP} \cdot \overline{BP} \) es:
$$ |x'y'| = \frac{a^2}{2} $$
De donde se deduce que:
$$ x'y' = \pm \frac{a^2}{2} $$
Llamando \( k = \frac{a^2}{2} \), podemos escribir simplemente:
$$ x'y' = \pm k $$
Es decir, en el sistema (x', y') las coordenadas están relacionadas mediante una proporcionalidad inversa.
Ejemplo práctico
Consideremos la hipérbola:
$$ xy = - \frac{1}{2} $$
Aquí, la constante es \( k = -\frac{1}{2} \), un valor negativo, por lo que la curva se encuentra en los cuadrantes segundo y cuarto.

Los ejes x e y actúan como asíntotas de la hipérbola, mientras que las bisectrices se convierten en sus ejes principal y secundario.
Como \( k < 0 \), el eje transversal es \( y = -x \).
Las coordenadas de los vértices son:
$$ A_1\left(-\sqrt{-k}, \sqrt{-k}\right) = \left(-\sqrt{\frac{1}{2}}, \sqrt{\frac{1}{2}}\right) $$
$$ A_2\left(\sqrt{-k}, -\sqrt{-k}\right) = \left(\sqrt{\frac{1}{2}}, -\sqrt{\frac{1}{2}}\right) $$
La longitud del semieje transversal es:
$$ a = \sqrt{2|k|} = \sqrt{2 \cdot \frac{1}{2}} = 1 $$
Y las coordenadas de los focos son:
$$ F_1\left(-\sqrt{-2k}, \sqrt{-2k}\right) = (-1, 1) $$
$$ F_2\left(\sqrt{-2k}, -\sqrt{-2k}\right) = (1, -1) $$
Representación gráfica:

Demostración. Partamos de una hipérbola equilátera con eje transversal sobre el eje x, cuya ecuación canónica es $$ x^2 - y^2 = 1 $$. Si rotamos el sistema 45° mediante la matriz:
$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} $$
Obtenemos:
$$ x' = \frac{\sqrt{2}}{2}(x - y), \quad y' = \frac{\sqrt{2}}{2}(x + y) $$
Sustituyendo en la ecuación original:
$$ x'^2 - y'^2 = \left( \frac{\sqrt{2}}{2}(x - y) \right)^2 - \left( \frac{\sqrt{2}}{2}(x + y) \right)^2 = 1 $$
Desarrollando:
$$ \frac{1}{2}(x^2 - 2xy + y^2) - \frac{1}{2}(x^2 + 2xy + y^2) = 1 $$
$$ \frac{1}{2}(x^2 + y^2 - 2xy - x^2 - y^2 - 2xy) = 1 $$
$$ -2xy = 1 \quad \Rightarrow \quad xy = -\frac{1}{2} $$
Así demostramos que la ecuación de la hipérbola tras la rotación es: $$ xy = -\frac{1}{2} $$

Notas
A continuación, se presentan algunas observaciones y consideraciones adicionales sobre las hipérbolas equiláteras:
-
La ecuación de una hipérbola equilátera con asíntotas paralelas a los ejes coordenados puede expresarse como \( (x - x_0)(y - y_0) = \pm 1 \); en el caso particular en que las asíntotas coinciden con los propios ejes cartesianos, se reduce a \( xy = \pm 1 \). Esta expresión constituye un caso particular de una función homográfica, cuya forma general es: $$ y = \frac{ax + b}{cx + d} $$ con \( c \ne 0 \) y \( ad - bc \ne 0 \). El centro de la hipérbola se encuentra en \( C\left( -\frac{d}{c}, \frac{a}{c} \right) \), y sus asíntotas son las rectas \( x = -\frac{d}{c} \) y \( y = \frac{a}{c} \).
Si se anula el coeficiente \( c \), o bien si se verifica \( ad - bc = 0 \), la función deja de representar una hipérbola y degenera en una recta.
Ejemplo: Consideremos la hipérbola equilátera de ecuación $$ xy = 1 $$ centrada en el origen y con asíntotas alineadas con los ejes coordenados. Supongamos ahora que trasladamos su centro al punto \( C(2;3) \).
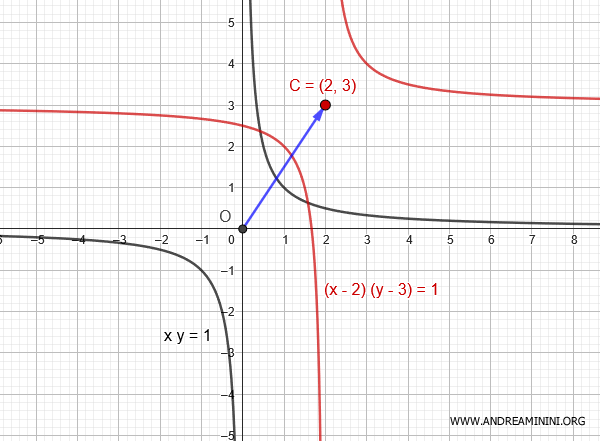
Cada punto de la curva se desplaza en la misma dirección y magnitud: $$ \begin{cases} x' = x + 2 \\ \\ y' = y + 3 \end{cases} $$ Resolviendo en función de las variables originales: $$ \begin{cases} x = x' - 2 \\ \\ y = y' - 3 \end{cases} $$ Sustituyendo en la ecuación original \( xy = 1 \): $$ (x' - 2)(y' - 3) = 1 $$ Eliminando los apóstrofos para simplificar la notación: $$ (x - 2)(y - 3) = 1 $$ Esta es la ecuación de una hipérbola equilátera con centro en \( C(2;3) \) y asíntotas paralelas a los ejes cartesianos, ubicadas en \( x = 2 \) y \( y = 3 \). Para expresar la ecuación en forma explícita, despejamos \( y \):
$$ (x - 2)(y - 3) = 1 $$ $$ xy - 3x - 2y + 6 = 1 $$ $$ y(x - 2) = 3x - 5 $$ $$ y = \frac{3x - 5}{x - 2} $$ Esta expresión corresponde a una función homográfica del tipo: $$ y = \frac{ax + b}{cx + d} $$ con \( a = 3 \), \( b = -5 \), \( c = 1 \), \( d = -2 \). Se cumplen claramente las condiciones \( c \ne 0 \) y \( ad - bc \ne 0 \), lo que confirma que la curva es efectivamente una hipérbola centrada en \( C(2;3) \), con asíntotas ubicadas en: $$ x = -\frac{d}{c} = -\left(-\frac{2}{1}\right) = 2 $$ $$ y = \frac{a}{c} = \frac{3}{1} = 3 $$
Y así sucesivamente.