Ecuación de la recta tangente en un punto de una hipérbola

La fórmula de la tangente permite determinar la ecuación de la recta tangente a una hipérbola en un punto dado $ P(x_0; y_0) $: $$ \frac{xx_0}{a^2} - \frac{yy_0}{b^2} = \pm 1 $$

Esta expresión se obtiene a partir de la ecuación canónica de la hipérbola $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 $$ sustituyendo $ x^2 \rightarrow xx_0 $ y $ y^2 \rightarrow yy_0 $.

Se trata de una aplicación directa de las fórmulas generales de tangentes a las cónicas, particularizada para el caso de la hipérbola.

Nota: Esta fórmula solo es válida si el punto $ P $ pertenece a la hipérbola. No puede aplicarse si el punto es exterior a la curva.

Ejemplo práctico

Consideremos la siguiente hipérbola:

$$ \frac{x^2}{4} - \frac{y^2}{3} = 1 $$

Queremos hallar la recta tangente a la curva en el punto $ P(4; 3) $.

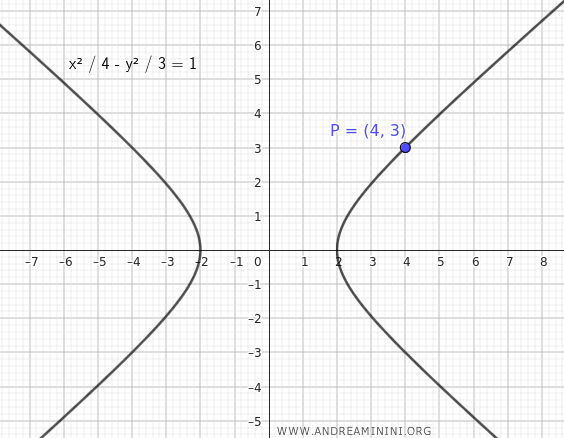
ejemplo de hipérbola

En primer lugar, comprobamos que el punto $ P $ pertenece a la hipérbola sustituyendo sus coordenadas en la ecuación:

$$ \frac{x^2}{4} - \frac{y^2}{3} = 1 $$

$$ \frac{4^2}{4} - \frac{3^2}{3} = 1 $$

$$ 4 - 3 = 1 $$

$$ 1 = 1 $$

La igualdad se verifica, así que el punto $ P(4; 3) $ pertenece efectivamente a la hipérbola.

Confirmado esto, aplicamos la fórmula de la tangente sustituyendo $ x^2 \rightarrow xx_0 $ y $ y^2 \rightarrow yy_0 $ en la ecuación original:

$$ \frac{x^2}{4} - \frac{y^2}{3} = 1 \quad \longrightarrow \quad \frac{xx_0}{4} - \frac{yy_0}{3} = 1 $$

Dado que el punto de tangencia es $ P(4; 3) $, sustituimos $ x_0 = 4 $ y $ y_0 = 3 $:

$$ \frac{x \cdot 4}{4} - \frac{y \cdot 3}{3} = 1 $$

$$ x - y = 1 $$

$$ y = x - 1 $$

Por tanto, la ecuación de la recta tangente a la hipérbola en el punto $ P(4; 3) $ es: $ y = x - 1 $.

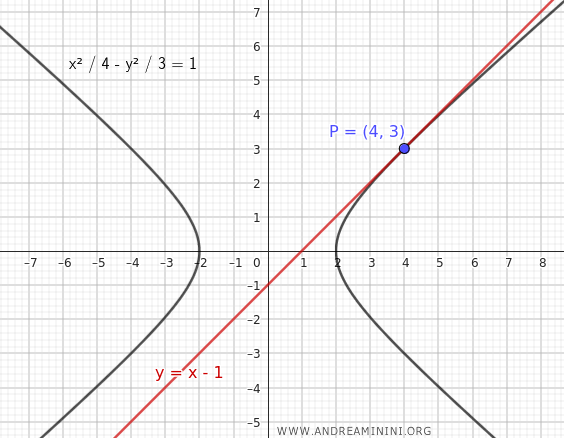
recta tangente en el punto P sobre la hipérbola

Así se determina de forma directa la recta tangente a una hipérbola en un punto conocido de la curva.