Ecuación de una hipérbola a partir de un punto y un vértice
Cuando se conocen las coordenadas de un punto $ P(x_0;y_0) $ y de uno de los vértices A o B de una hipérbola centrada en el origen, es posible determinar su ecuación siguiendo estos pasos:
Dado que no se dispone de la posición de los focos, no se puede saber de antemano si el eje mayor de la hipérbola es horizontal o vertical. Por tanto, hay que contemplar ambas posibilidades:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = \pm 1 $$
Se sustituyen en la ecuación las coordenadas del punto y del vértice conocidos.
A continuación, se resuelve la ecuación para determinar el otro vértice.
Ejemplo
En este ejercicio se pide encontrar la ecuación de una hipérbola con centro en el origen de los ejes cartesianos, con un vértice real en $ A( \sqrt{5};0 ) $ y que pasa por el punto $ P(- \frac{5}{2};1) $.
El vértice real se encuentra sobre el eje x, lo que indica que el eje mayor - donde se sitúan los focos de la hipérbola - es horizontal.
En consecuencia, la ecuación de la hipérbola es:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
La reescribimos en una forma más conveniente para los cálculos que siguen:
$$ \frac{b^2x^2-a^2y^2}{a^2b^2} = 1 $$
$$ b^2x^2-a^2y^2 = a^2b^2 $$
Sustituimos las coordenadas del punto conocido $ P(- \frac{5}{2};1) $ en la ecuación de la hipérbola, es decir, $ x= - \frac{5}{2} $ y $ y=1 $:
$$ b^2 \cdot (- \frac{5}{2})^2-a^2 \cdot(1)^2 = a^2b^2 $$
$$ \frac{25}{4} b^2 -a^2 = a^2b^2 $$
$$ \frac{25}{4}b^2 -a^2 = a^2b^2 $$
Ahora sustituimos las coordenadas del vértice $ A(a;0)=( \sqrt{5};0 ) $, lo que implica que $ a=\sqrt{5} $:
$$ \frac{25}{4}b^2 -( \sqrt{5} )^2 = ( \sqrt{5} )^2b^2 $$
$$ \frac{25}{4}b^2 - 5 = 5b^2 $$
$$ \frac{25}{4}b^2 - 5b^2 = 5 $$
$$ \frac{25b^2 - 20b^2}{4} = 5 $$
$$ \frac{5b^2}{4} = 5 $$
$$ b^2 = 5 \cdot \frac{4}{5} $$
$$ b^2 = 4 $$
Por tanto, si $ b^2 = 4 $, el semieje menor tiene valor $ b=2 $.
En este punto, sustituimos $ a= \sqrt{5} $ y $ b=2 $ en la ecuación canónica de la hipérbola:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{(\sqrt{5})^2} - \frac{y^2}{2^2} = 1 $$
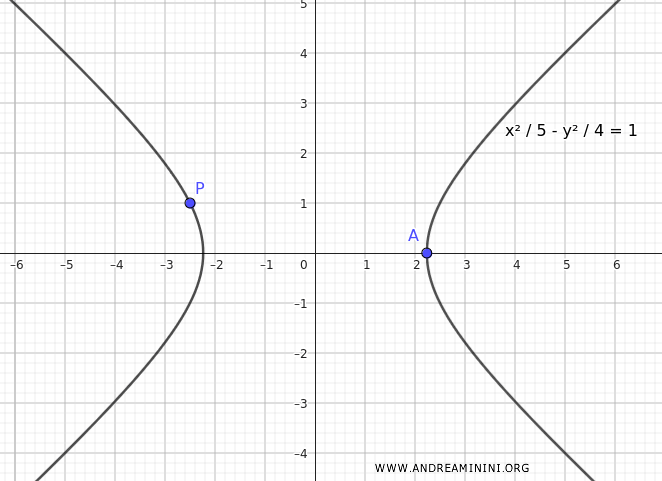
$$ \frac{x^2}{5} - \frac{y^2}{4} = 1 $$
Esta es la ecuación de la hipérbola centrada en el origen, con vértice real en $ A( \sqrt{5};0 ) $ y que pasa por el punto $ P(- \frac{5}{2};1) $.
Y así sucesivamente.