Ecuación de una hipérbola que pasa por dos puntos

Para determinar la ecuación de una hipérbola con centro en el origen que pase por dos puntos dados $ P_1(x_1;y_1) $ y $ P_2(x_2;y_2) $, se siguen los pasos siguientes:

En primer lugar, es necesario identificar el eje transversal, es decir, el eje sobre el cual se sitúan los focos:

• Si el eje transversal es el eje x, la ecuación canónica de la hipérbola es $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
• Si el eje transversal es el eje y, la ecuación correspondiente es $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$

Si el enunciado no especifica con claridad cuál es el eje transversal, conviene analizar ambas opciones.

A continuación, se sustituyen las coordenadas de los puntos dados $ P_1(x_1;y_1) $ y $ P_2(x_2;y_2) $ en la ecuación estándar, obteniendo así un sistema de ecuaciones que permitirá determinar los valores de $ a^2 $ y $ b^2 $.

Ejemplo práctico

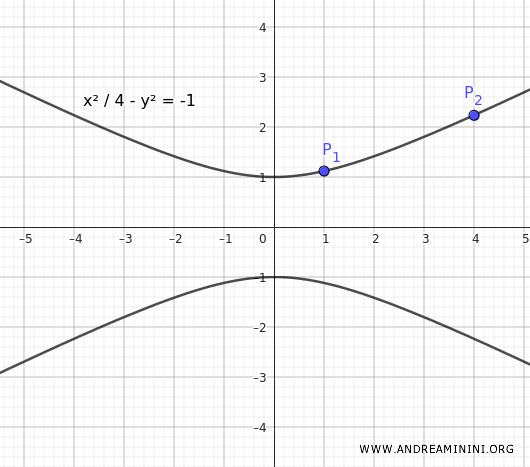
Consideremos una hipérbola con focos situados sobre el eje y, que pasa por los puntos $ P_1(1; \frac{\sqrt{5}}{2}) $ y $ P_2(4;\sqrt{5}) $.

Dado que los focos están sobre el eje y, la ecuación canónica de la hipérbola es:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$

Procedemos entonces a sustituir las coordenadas de los puntos conocidos en dicha ecuación, lo que nos conduce al siguiente sistema:

$$ \begin{cases} \frac{x_1^2}{a^2} - \frac{y_1^2}{b^2} = -1 \\ \\ \frac{x_2^2}{a^2} - \frac{y_2^2}{b^2} = -1 \end{cases} $$

$$ \begin{cases} \frac{1^2}{a^2} - \frac{(\frac{\sqrt{5}}{2})^2}{b^2} = -1 \\ \\ \frac{4^2}{a^2} - \frac{(\sqrt{5})^2}{b^2} = -1 \end{cases} $$

$$ \begin{cases} \frac{1}{a^2} - \frac{\frac{5}{4}}{b^2} = -1 \\ \\ \frac{16}{a^2} - \frac{5}{b^2} = -1 \end{cases} $$

$$ \begin{cases} \frac{1}{a^2} - \frac{5}{4b^2} = -1 \\ \\ \frac{16b^2 - 5a^2}{a^2b^2} = -1 \end{cases} $$

$$ \begin{cases} \frac{4b^2 - 5a^2}{4a^2b^2} = -1 \\ \\ 16b^2 - 5a^2 = -a^2b^2 \end{cases} $$

Ahora resolvemos el sistema: aislamos $ b^2 $ en la primera ecuación y lo sustituimos en la segunda.

$$ \begin{cases} 4b^2 + 4a^2b^2 = 5a^2 \\ \\ 16b^2 - 5a^2 = -a^2b^2 \end{cases} $$

$$ \begin{cases} b^2(4 + 4a^2) = 5a^2 \\ \\ 16b^2 - 5a^2 = -a^2b^2 \end{cases} $$

$$ \begin{cases} b^2 = \frac{5a^2}{4 + 4a^2} \\ \\ 16b^2 - 5a^2 = -a^2b^2 \end{cases} $$

$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ 16b^2 - 5a^2 = -a^2b^2 \end{cases} $$

$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ 16 \cdot \frac{5a^2}{4 + 4a^2} - 5a^2 = -a^2 \cdot \frac{5a^2}{4 + 4a^2} \end{cases} $$

$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ \frac{80a^2 - 5a^2(4 + 4a^2)}{4 + 4a^2} = -\frac{5a^4}{4 + 4a^2} \end{cases} $$

Multiplicamos ambos miembros de la segunda ecuación por $ 4 + 4a^2 $ y simplificamos:

$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ 80a^2 - 20a^2 - 20a^4 + 5a^4 = 0 \end{cases} $$

$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ -15a^4 + 60a^2 = 0 \end{cases} $$

$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ a^2(60 - 15a^2) = 0 \end{cases} $$

$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ 3a^2(20 - 5a^2) = 0 \end{cases} $$

La segunda ecuación tiene dos soluciones: $ a = 0 $ y $ a = \sqrt{\frac{20}{5}} = \sqrt{4} = 2 $.

Dado que una longitud no puede ser nula, descartamos la solución $ a = 0 $ y nos quedamos con la raíz positiva: $ a = 2 $.

Conocido el valor del semieje transversal, sustituimos $ a = 2 $ en la expresión de $ b $ para determinar su valor:

$$ \begin{cases} b = \sqrt{ \frac{5 \cdot 2^2}{4 + 4 \cdot 2^2} } \\ \\ a = 2 \end{cases} $$

$$ \begin{cases} b = \sqrt{ \frac{20}{4 + 16} } \\ \\ a = 2 \end{cases} $$

$$ \begin{cases} b = \sqrt{ \frac{20}{20} } \\ \\ a = 2 \end{cases} $$

$$ \begin{cases} b = \sqrt{1} \\ \\ a = 2 \end{cases} $$

$$ \begin{cases} b = 1 \\ \\ a = 2 \end{cases} $$

Por tanto, los semiejes de la hipérbola son $ a = 2 $ y $ b = 1 $.

Finalmente, al sustituir estos valores en la ecuación estándar obtenemos:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$

$$ \frac{x^2}{2^2} - \frac{y^2}{1^2} = -1 $$

$$ \frac{x^2}{4} - y^2 = -1 $$

Esta es la ecuación de la hipérbola con focos sobre el eje y que pasa por los puntos $ P_1(1; \frac{\sqrt{5}}{2}) $ y $ P_2(4;\sqrt{5}) $.

Y así continúa.