Cómo hallar la ecuación de una hipérbola a partir de un punto y una recta tangente

Para encontrar la ecuación de una hipérbola con centro en el origen, conociendo un punto sobre ella $ P(x,y) $ y la ecuación de una recta tangente, sigue estos pasos:

En primer lugar, determina si el eje transverso está alineado con el eje x $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ o con el eje y $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$, según los datos proporcionados.
Luego, sustituye las coordenadas del punto $ P(x,y) $ en la ecuación general de la hipérbola.
Compara la ecuación de la recta tangente con la forma estándar de una tangente a la hipérbola: $ \frac{x_0x}{a^2} - \frac{y_0y}{b^2} = 1 $. A partir de allí, identifica las coordenadas del punto de tangencia $ (x_0, y_0) $ en función de $ a^2 $ y $ b^2 $, y sustituye en consecuencia.
Finalmente, plantea un sistema de ecuaciones que te permita resolver $ a^2 $ y $ b^2 $.

Un ejemplo práctico

Considera una hipérbola centrada en el origen cuyo eje transverso está sobre el eje x. Supongamos que pasa por el punto $ P(-4,3) $ y que tiene por tangente la recta $ x - y = 1 $.

Como el eje transverso está sobre el eje x, su ecuación estándar es:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

Dado que la hipérbola pasa por el punto $P(-4, 3)$, sustituimos $x = -4$ y $y = 3$ en la ecuación anterior, obteniendo:

$$ \frac{16}{a^2} - \frac{9}{b^2} = 1 \quad \text{(Ecuación 1)} $$

Además, sabemos que la recta tangente está dada por $x - y = 1$.

Recordemos que la ecuación general de la recta tangente a una hipérbola en el punto $(x_0, y_0)$ es:

$$ \frac{x_0x}{a^2} - \frac{y_0y}{b^2} = 1 $$

Al comparar esta expresión con la tangente dada $x - y = 1$, identificamos:

$$ \underbrace{ \frac{x_0}{a^2} }_1 x - \underbrace{ \frac{y_0}{b^2} }_1 y = 1 \Leftrightarrow x - y = 1 $$

Para que los coeficientes de $x$ y $y$ coincidan, debe cumplirse que:

$$ \frac{x_0}{a^2} = 1 \quad \text{y} \quad -\frac{y_0}{b^2} = -1 $$

De aquí se deduce que:

$$ x_0 = a^2 \quad \text{y} \quad y_0 = b^2 $$

Así, el punto de tangencia sobre la hipérbola es $(a^2, b^2)$.

Como esta es la tangente en dicho punto, al sustituir $x = a^2$ y $y = b^2$ en la ecuación $x - y = 1$, se obtiene:

$$ a^2 - b^2 = 1 \quad \text{(Ecuación 2)} $$

Ahora disponemos de un sistema de dos ecuaciones con dos incógnitas:

$$ \begin{cases} \frac{16}{a^2} - \frac{9}{b^2} = 1 \\ \\ a^2 - b^2 = 1 \end{cases} $$

Despejamos $ a^2 $ en la segunda ecuación:

$$ a^2 = b^2 + 1 $$

Sustituyendo esta expresión en la primera ecuación:

$$ \frac{16}{b^2 + 1} - \frac{9}{b^2} = 1 $$

$$ \frac{16b^2 - 9(b^2 + 1)}{b^2(b^2 + 1)} = 1 $$

Multiplicamos ambos miembros por $b^2(b^2 + 1)$ para eliminar los denominadores:

$$ 16b^2 - 9(b^2 + 1) = b^4 + b^2 $$

Desarrollando y reordenando los términos:

$$ 16b^2 - 9b^2 - 9 = b^4 + b^2 $$

$$ 7b^2 - 9 = b^4 + b^2 $$

$$ b^4 - 6b^2 + 9 = 0 $$

Si llamamos $u = b^2$, esta ecuación se transforma en:

$$ u^2 - 6u + 9 = 0 $$

Que se factoriza como:

$$ (u - 3)^2 = 0 $$

Luego, $u = 3$, lo que implica $b^2 = 3$.

Y por tanto:

$$ \begin{cases} b^2 = 3 \\ \\ a^2 = b^2 + 1 \end{cases} $$

Sustituyendo, se obtiene:

$$ a^2 = 4 $$

En conclusión, con $ a^2 = 4 $ y $ b^2 = 3 $, la ecuación de la hipérbola es:

$$ \frac{x^2}{4} - \frac{y^2}{3} = 1 $$

Esta es la ecuación de la hipérbola que pasa por el punto $(-4, 3)$ y cuya tangente es la recta $x - y = 1$.

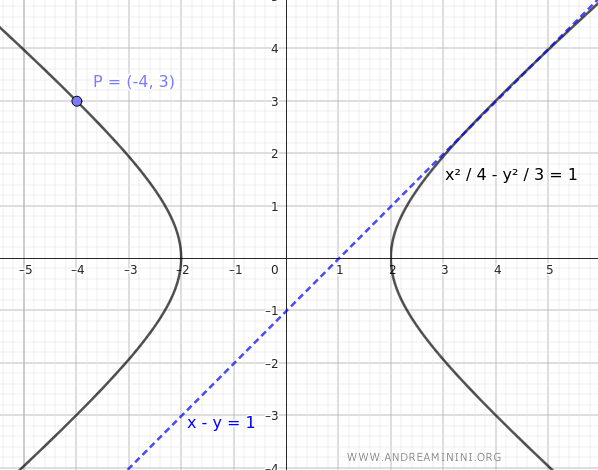
hyperbola graph

Así es como se resuelve el problema paso a paso.