Ecuación de una hipérbola a partir de un asíntota y un vértice
Para determinar la ecuación de una hipérbola con centro en el origen, conociendo uno de sus asíntotas y un vértice $ A(a;0) $ o $ B(0;b) $, sigue estos pasos:
- Establece si el eje transverso es horizontal o vertical, en función de los datos proporcionados. Esto te permitirá escoger la forma adecuada de la ecuación de la hipérbola. Si no se puede determinar directamente, considera ambas posibilidades: $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 $$
- Escribe la ecuación del asíntota: $$ y = \pm \frac{b}{a} x $$ y sustituye el valor conocido del semieje ($ a $ o $ b $).
- Resuelve el sistema de ecuaciones resultante para hallar el semieje desconocido.
Una vez conocidos los valores de $ a $ y $ b $, podrás escribir la ecuación completa de la hipérbola.
Un ejemplo práctico
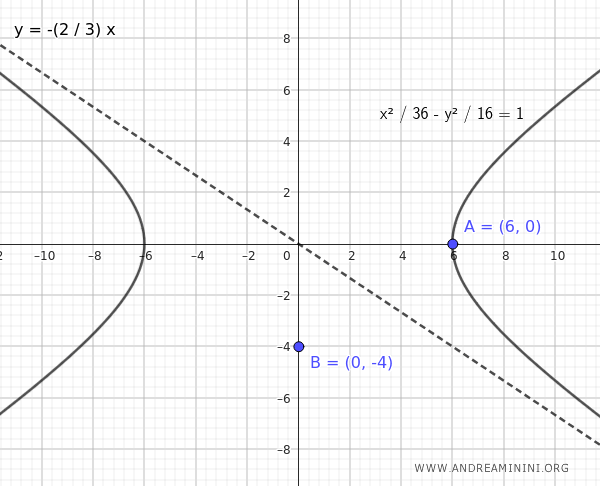
Veamos una hipérbola cuyo vértice real está en el punto $ A(6;0) $, y que tiene un asíntota con ecuación $ y = - \frac{2}{3} x $.
Como se indica que el vértice $ A(6;0) $ es “real”, significa que se encuentra sobre el eje transverso, el cual también contiene a los focos.
Esto implica que el eje transverso coincide con el eje x, por lo tanto la ecuación de la hipérbola tendrá la siguiente forma:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
Planteamos ahora un sistema de ecuaciones utilizando la ecuación del asíntota y la de la hipérbola:
$$ \begin{cases} y = \frac{b}{a} x \\ \\ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \end{cases} $$
Sabemos que el vértice $ A(6;0) $ se encuentra sobre el eje x, a una distancia de $ a = 6 $ unidades respecto al centro de la hipérbola.
Al sustituir $ a = 6 $, obtenemos:
$$ \begin{cases} y = \frac{b}{6} x \\ \\ \frac{x^2}{6^2} - \frac{y^2}{b^2} = 1 \end{cases} $$
Lo que se simplifica como:
$$ \begin{cases} y = \frac{b}{6} x \\ \\ \frac{x^2}{36} - \frac{y^2}{b^2} = 1 \end{cases} $$
Sabemos que el asíntota es $ y = - \frac{2}{3} x $.
Igualamos entonces las expresiones:
$$ \begin{cases} - \frac{2}{3} x = \frac{b}{6} x \\ \\ \frac{x^2}{36} - \frac{y^2}{b^2} = 1 \end{cases} $$
Dividimos ambos miembros de la primera ecuación entre $ x $ (suponiendo $ x \ne 0 $) y simplificamos:
$$ \begin{cases} - \frac{2}{3} = \frac{b}{6} \\ \\ \frac{x^2}{36} - \frac{y^2}{b^2} = 1 \end{cases} $$
Despejamos $ b $ a partir de la primera ecuación:
$$ \begin{cases} b = - \frac{2}{3} \cdot 6 \\ \\ \frac{x^2}{36} - \frac{y^2}{b^2} = 1 \end{cases} $$
Y obtenemos:
$$ \begin{cases} b = -4 \\ \\ \frac{x^2}{36} - \frac{y^2}{b^2} = 1 \end{cases} $$
Sustituimos $ b = -4 $ en la segunda ecuación:
$$ \begin{cases} y = \frac{b}{6} x \\ \\ \frac{x^2}{36} - \frac{y^2}{(-4)^2} = 1 \end{cases} $$
Y simplificamos finalmente:
$$ \begin{cases} y = \frac{b}{6} x \\ \\ \frac{x^2}{36} - \frac{y^2}{16} = 1 \end{cases} $$
Por lo tanto, la ecuación de la hipérbola es:
$$ \frac{x^2}{36} - \frac{y^2}{16} = 1 $$
Esta es la ecuación de la hipérbola que tiene vértice real en $ A(6;0) $ y asíntota $ y = - \frac{2}{3} x $.
Y así continúa el procedimiento.